1.5 数据分析的思维技巧（多维法）

点击查看【bilibili】

多维法：多个维度数据的汇总

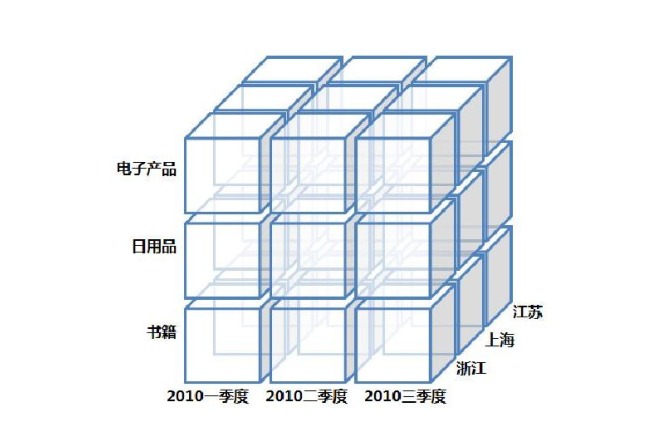
用户统计维度：性别、年龄…
用户行为维度：注册用户、用户偏好、用户兴趣、用户流失…
消费维度：消费金额、消费频率、消费水平…
商品维度：商品品类、商品品牌、商品属性…

多维法的缺点：辛普森悖论

下表显示，数据汇总后：女生的录取率 > 男生的录取率

但若拆分来看，每个学院，女生的录取率 < 男生的录取率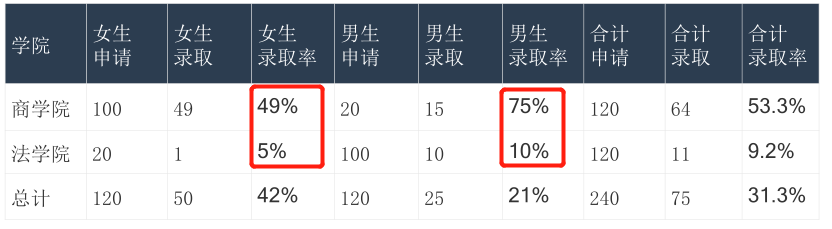

• 解决辛普森悖论的方法：钻取。也就是将聚类细分。

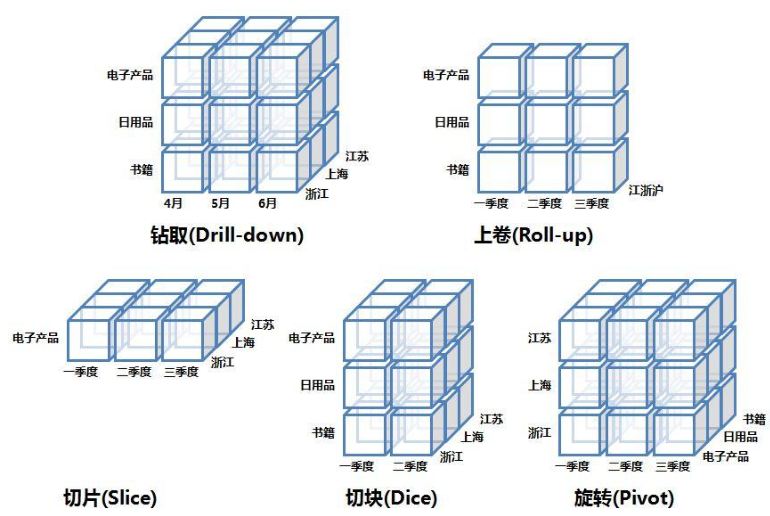
以下内容摘自知乎：统计|辛普森悖论

• 举例

P大、T大，2所学校，男女生比例：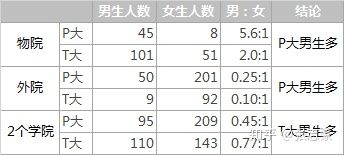

这种违背常理的情况被称为“辛普森悖论”。虽然这么叫，但其实这不是个真正的悖论，它内部没有包含逻辑上的矛盾，只是有些违背人们的常理。

• 理解

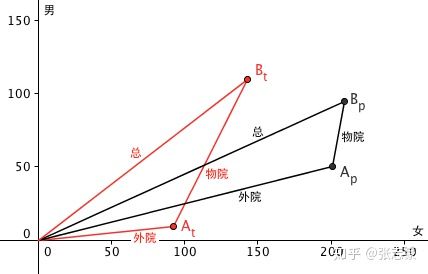
用几何图形来帮助理解：

图中，黑色的线代表 P 大数据，红色的线代表 T 大的数据。A p 点的横坐标为 P 大外院女生人数，纵坐标为 P 大外院男生人数；B p 点的横纵坐标则分别为 P 大总女生人数和总男生人数。A t 和 B t 点的意义与之相对应。
设坐标原点为 O，则 OA p 的斜率表示的就是 P 大外院的男女比例，A p B p 表示的是 P 大物院的男女比例，OB p 表示的则是 P 大总男女比例；T 大的各线段斜率意义与之对应。

如此一来，一切都变得清晰起来了。辛普森悖论反映在这张图上，就成了一个显然的事实：在 P 大的外院、物院两个向量的斜率分别大于 T 大的两个向量的斜率的条件下，总人数向量的斜率当然不一定哪个大呀！根据这个直观的理解，可以随意编造能产生辛普森悖论的数据。

• 解决

对关键变量，特别是直接影响被解释变量的变量，一定要对其进行细分，才能得到正确的结论。

多维法总结

• 核心：多维法是一种精细驱动的思维。
• 优点：处理大数据，对于维度丰富较复杂的数据有较好的效果。但若维度过多，会消耗时间较多。
• 应用：只要数据齐全、维度较多，均可使用。
• 注意：辛普森悖论。