客观世界的实际问题中非常多随机变量都服从或近似于正态分布,它在数理统计中有重要意义.
1. 密度函数与分布函数
标准正态分布
| 概率密度函数 | 若随机变量X的概率密度函数为 则称X服从标准正态分布,记作,这是一个偶函数 |
|---|---|
| 概率分布函数 | |
| 性质 |
一般正态分布
| 概率密度函数 | |
|---|---|
| 概率分布函数 | |
| 密度曲线f(x)性质 |   |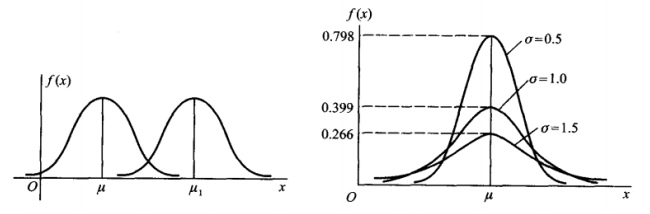
2. 数字特征与线性性质**
3. 二维正态分布
当(X,Y)有如下密度函数则称(X,Y)服从二维正态分布,记作
此时X,Y的边缘分布满足
由上,XY独立的充要条件即r=0
此外
的充要条件是
若有收获，就点个赞吧
0 人点赞
