算法描述
- 对于不等长字符串,应该考虑从左到右遍历字符
高位优先字符串排序中count[]的意义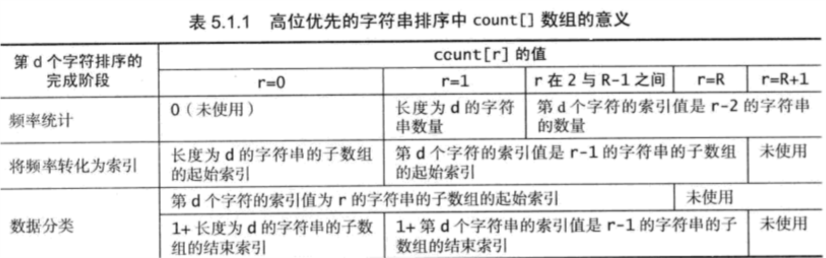
实现
import edu.princeton.cs.algs4.Insertion;public class MSD {private static int R = 256;//基数private static final int M = 15;//小数组插入排序的阈值private static String[] aux;//辅助数组private static int charAt(String s, int d){if (d < s.length()) return s.charAt(d);else return -1;}public static void sort(String[] a){int N = a.length;aux = new String[R+1];sort(a,0, N-1, 0);}private static boolean less(String[] a, int v, int w, int d){return a[v].charAt(d) < a[v].charAt(d);}private static void sort(String[] a, int lo, int hi, int d){if (hi <= lo + M){//小数组,插入排序Insertion(a, lo, hi, d);return;}int [] count = new int[R+2];for (int i = lo; i <= hi; i++)//计算频度count[charAt(a[i],d) + 2]++;for (int r = 0; r < R; r++)//转换为索引count[r+1] += count[r];for (int i = lo; i <= hi; i++)//数据分类aux[count[charAt(a[i], d)+1]++] = a[i];for (int i = lo; i <= hi; i++)//回写a[i] = aux[i];//递归的以每个字符为键进行排序for (int r = 0; r < R; r++)sort(a, lo+count[r], lo+count[r+1]-1, d+1);}}
- 首字母排序以及整体递归情况

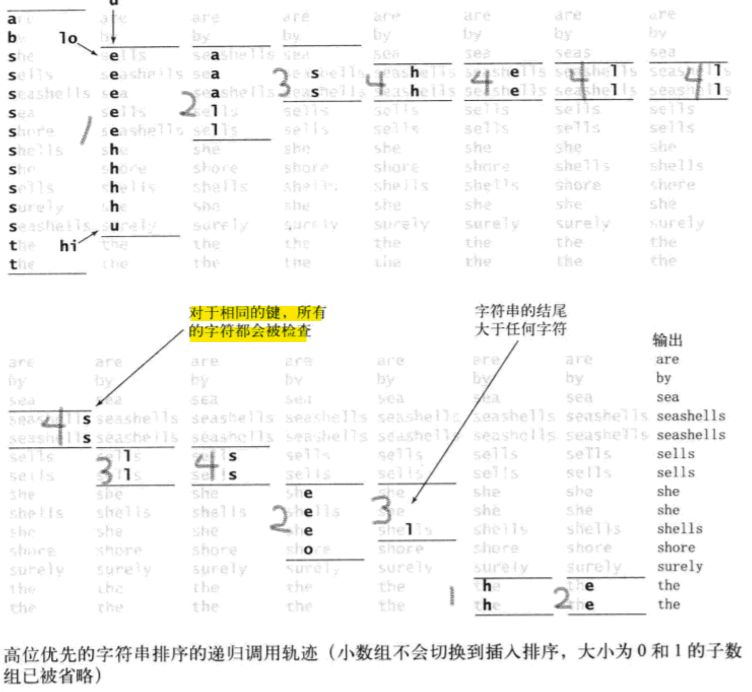
算法弊端
- 小数组问题:随着递归深入,最终每个字符串都会遇到hi==lo即大小为1的子数组,若不进行处理:
- 每次count[]都需要初始化为0
- 还需进行R次索引转换(无意义)
因此需要设置阈值M作为进行小数组插入排序的门槛,且为了避免检查已知相同的字符所带来的的成本 - 使用假设前d个字符均相同的插入排序
private static boolean less(String v, String w, int d){return v.substring(d).compareTo(w.substring(d)) < 0;}private static void exch(String[] a, int v, int w){String temp = a[v];a[v] = a[w];a[w] = temp;}//假设前d个字符相同的插入排序private static void Insertion(String[] a, int lo, int hi, int d){for(int i = lo; i <= hi; i++){for (int j = i; j > lo && less(a[j],a[j-1],d); j--)exch(a,j,j-1);}}
- 等值键:如上图,等值键的所有字符都会被检查,开销不小
- 额外空间:MSD使用了两个辅助数组aux[]和count[],aux[]大小为N且在递归外创建,但每层递归都会创建count[R+2],这部分空间直到递归结束才会释放
算法分析
- MSD算法中字符串的顺序不重要,每个字符串值的情况决定了开销
- 随机字符串:亚线性
- 非随机且有重复:接近线性时间
- 最坏情况(N个完全相同字符串):线性时间
- 命题:对基于R个字符的字母表的N个字符串排序,MSD平均需要检查NlogN个字符
- 时间:对基于R个字符的字母表的N个字符串排序,MSD访问数组的次数在8N+3R到~7wN+3wR之间,w为字符平均长度
证明:最好情况,首字母全不不同,只需一遍就能排好序,最坏情况下和LSD类似
- 空间:对基于R个字符的字母表的N个字符串排序,MSD最坏时需要空间~Rw+N
证明:aux[N]在递归外创建,count[R+2]每层递归创建一个,递归最深w层
- 根据3,当小数组处理选择M时,应R与M²成正比
证明:当M作阈值,可分为N/M组,插入排序需要比较(M²/4*N/M=MN/4)次,而MSD会访问数组NR/M次,以比较换访问,当MN/4
M²/4

