Ch7 数理统计基础

前六章概率论部分研究了随机变量的统计规律性,然而现实问题中随机变量的分布基本都是未知的,数理统计就是抽取一小部分产品/元件做试验,使用试验结果确定总体随机变量的分布情况

1. 总体与样本

设随机变量独立同分布,则称为一样本容量为n的来自总体X的样本,而的取值为样本观测值
从总体中抽取的样本应该满足随机性&独立性,则:

2. 基本分布

构成了数理统计中四个重要的基本分布,Ch5中已经介绍了正态分布

2.1 卡方分布

定义
表示
密度函数
数字特征
f(x)图像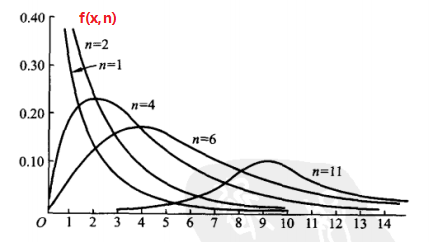
性质

2.2 t分布

定义
表示
密度函数
数字特征
f(x)图像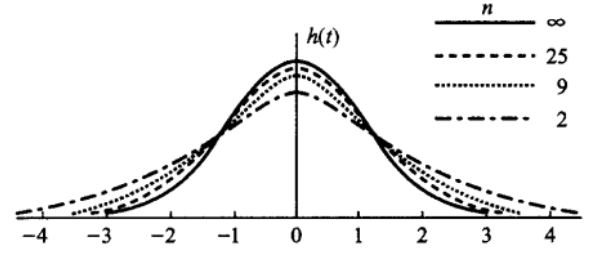
性质

2.3 F分布

定义
表示
密度函数
f(x)图像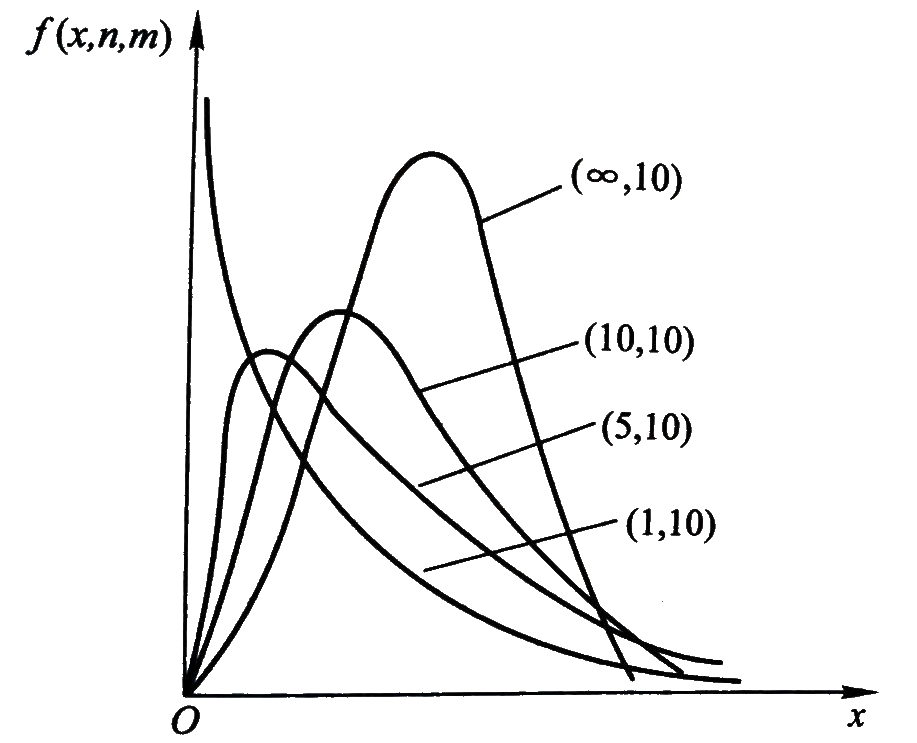

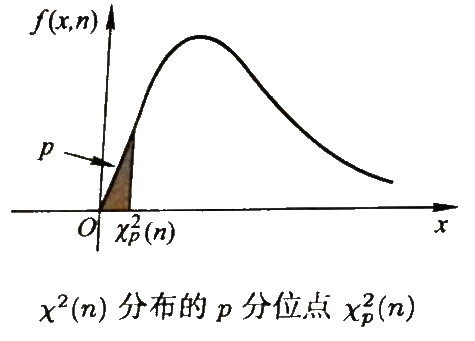
3. 分位点

通常分布已知时,
数理统计中,成立时的a(u**p**)
关于分位点,通常需要查表确定

分布	分位点	定义	图像

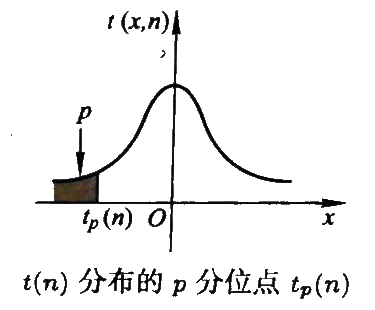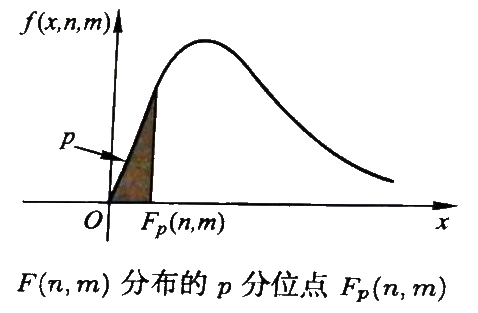4. 统计量

采集样本后需要对样本数据即观测值处理,构造样本的函数
:::info

• 
• ::: | 常用统计量 | | 观测值 | | :—-: | :—-: | —- | | 样本均值 | | | | 样本方差 | | | | 样本标准差 | | | | 样本k阶原点矩 | | | | 样本k阶中心矩 | | |

:::info

1. 和Ch4中的一般随机变量的方差等于二阶中心距不同,样本方差S不等于二阶样本中心距B
2. 样本原点矩/中心距对比随机变量原点矩/中心距

:::

5. 抽样分布定理

常用统计量和样本函数的分布被总结为抽样分布定理,以下定理都建立在样本独立基础上

5.1 一个正态总体下

• 定理1:正态分布线性性质

  

• 定理2:**构造自由度n-1的卡方分布**

  

• 定理3:**构造自**由度n-1的t分布

  

• 定理4:**构造符合要求的新随机变量**

  

  5.2 两个正态总体下

• 定理1:**上述定理1+正态分布可加性**

  

• 定理2:**构造自由度n1+n2-2的t分布**

  

• 定理3:**构造自由度(n1-1,n2-1)的t分布**