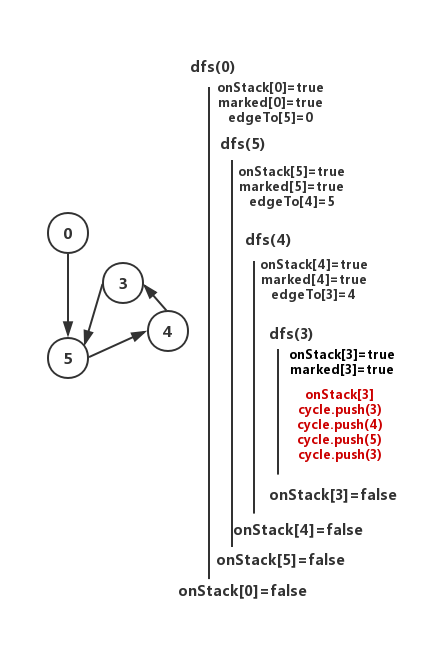
4.5.1 算法:有向环寻找

调度问题

优先级限制下的调度问题: 给定一组任务,以及一组任务完成先后次序的优先级限制,如何在满足限制的情况下完成所有任务

建立模型:建立有向图,任务作为结点,有向边对于优先级顺序

问题转化:拓扑排序,给定有向图,将所有顶点排序,使得所有有向边均从排在前的元素指向排在后的元素

有向图中的环

  • 如果一个优先级限制问题中存在环,问题无解(无论从哪个开始都不满足优先级顺序)
  • 有向环检测:确定图是有向无环图(DAG)才能解决优先级问题
  • 思路:使用DFS算法时,递归过程作为隐式栈表示当前正遍历的路径,一旦在找到v->w后发现w已经在栈中,说明是一个环

有向环API:public class DirectedCycle

返回类型 方法 描述
DirectedCycle(Digraph G) 构造函数
boolean hasCycle() G是否含有环
Iterable cycle() 环中所有顶点

实现

  1. public class DirectedCycle{
  2.     private boolean[] marked;
  3.     private int[] edgeTo;
  4.     private Stack<Integer> cycle;//有向环中所有结点
  5.     private boolean[] onStack;//栈,当为true表示当前隐式栈中已经有结点w
  7.     public DirectedCycle(Digraph G){
  8.         marked = new boolean[G.V()];
  9.         edgeTo = new int[G.V()];
  10.         onStack = new boolean[G.V()];
  11.         for(int v = 0; v < G.V(); v++){
  12.             if(!marked[v]) dfs(G,v);
  13.         }
  14.     }
  16.     private void dfs(Digraph G, int v){
  17.         onStack[v] = true;
  18.         marked[v] = true;
  19.         for(int w: G.adj(v)){
  20.             if(this.hasCycle()) return;//只要找到一个环即可
  21.             else if(!marked[w]){
  22.                 edgeTo[w] = v;
  23.                 dfs(G,w);
  24.             }
  25.             else if(onStack[w]){
  26.                 //条件1,marked[w]==true表示该结点已被访问
  27.                 //条件2,onStack[w]==true表示是当前隐式栈中
  28.                 //只满足前者可能是结点w作为两条路的终点被指向,但此时不构成环
  29.                 cycle = new Stack<Integer>();
  30.                 for(int x = v; x != w; x = edgeTo[w])
  31.                     cycle.push(x);//后访问的点先压入栈中
  32.                 cycle.push(w);
  33.                 cycle.push(v);
  34.             }
  35.         }
  36.         onStack[v] = false;//调用栈结束后onStack[v]=false即表示出栈
  37.     }
  39.     public boolean hasCycle(){ return cycle != null;}
  40.     public Iterable<Integer> cycle(){ return cycle;}
  41. }
  • 在执行dfs(G,v)时将onStack[v]设为true,表示进入该路径,调用结束时设回false,只有当前路径上marked[w]和onStack[w]同时满足才构成有向环

    示例

    DC.jpg

4.5.2 算法:三种不同的顶点排序

思考:既然DFS只会沿每条路径到头访问每个结点一次,那把dfs()的参数结点保存在某个数据结构,遍历该数据结构就能访问所有结点

模型:优先级限制的调度问题等价于计算有向无环图中所有顶点的拓扑顺序,DFS沿着有向边访问结点就是按照优先级访问 问题转化:综上,只需要按照某个顺序保存参数结点就可以得到所有顶点的拓扑顺序

结点保存顺序

  • pre()前序:dfs()前将顶点加入队列
  • post()后序:dfs()后将顶点加入队列

  • reversePost()逆后序:dfs()后将顶点压入栈

    示例

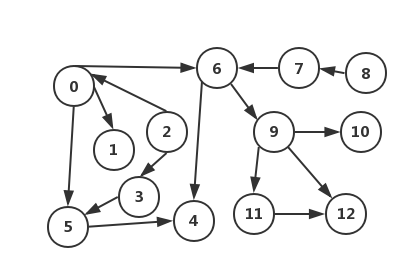
    order.jpg

  • pre:0-5-4-1-6-9-11-12-10-2-3-8-7

  • post:4-5-1-12-11-10-9-6-0-3-2-7-8
  • reversePost:8-7-2-3-0-6-9-10-11-12-1-5-4

实现

  1. public class DepthFirstOrder{
  2.     private boolean marked[];
  3.     private Queue<Integer> pre;//前序
  4.     private Queue<Integer> post;//后序
  5.     private Stack<Integer> reversePost;//逆后序
  7.     public DepthFirstOrder(Digraph G){
  8.         marked = new boolean[G.V()];
  9.         pre = new Queue<>();
  10.         post = new Queue<>();
  11.         reversePost = new Stack<>();
  12.         for(int v = 0; v < G.V(); v++)
  13.             if(!marked[v]) dfs(G,v);
  14.     }
  16.     private void dfs(Digraph G, int v){
  17.         pre.enqueue(v);
  18.         for(int w: G.adj(v))
  19.             if(!marked[w]) dfs(G,w);
  20.         post.enqueue(v);
  21.         reversePost.push(v);
  22.     }
  24.     public Iterable<Integer> pre(){ return pre;}
  25.     public Iterable<Integer> post(){ return post;}
  26.     public Iterable<Integer> reversePost(){ return reversePost;}
  27. }
  • 结论:拓扑排序是所有顶点的逆后序reversePost

证明:有向图中优先级v->w反映在函数中即为dfs(G,v){dfs(G,w)}的递归关系,在调用dfs(v)时只可能有下列三种情况:

  • dfs(w)已被调用返回
  • dfs(w)将被调用,且先于dfs(v)返回
  • dfs(w)已被调用,但未返回
    但最后一种情况不可能在无环有向图中出现,只有环才能满足条件.
    因此,v->w的优先级限制的v必须在w前被读出,逆后序总是先压入w,后压入v,读取时即v->w的拓扑顺序

算法4.5 拓扑排序

  1. import edu.princeton.cs.algs4.In;
  2. import edu.princeton.cs.algs4.StdOut;
  4. public class Topological{
  5.     private Iterable<Integer> order;//逆后序
  7.     public Topological(Digraph G){
  8.         DirectedCycle cycleFinder = new DirectedCycle(G);//有向环查找器
  9.         if(!cycleFinder.hasCycle()){
  10.             DepthFirstOrder dfs = new DepthFirstOrder(G);
  11.             order = dfs.reversePost();//逆后序
  12.         }
  13.     }
  15.     public Iterable<Integer> order(){ return order;}
  16.     public boolean isDAG(){ return order != null; }
  18.     public static void main(String[] args){
  19.         Digraph G = new Digraph(new In(args[0]));
  20.         Topological top = new Topological(G);
  21.         for(int v:top.order()) StdOut.println(v);//依次出栈打印即为拓扑排序
  22.     }
  23. }

算法分析

  • 命题:使用DFS对DAG进行拓扑排序的时间和V+E成正比

证明:第一遍DFS保证不存在有向环,第二遍DFS产生逆后序排列,每次DFS时访问了每个顶点和所有边

  • 最终的Topo顺序和构造有向图时结点插入顺序有关,同一幅DAG的Topo序列可能不同,但始终满足优先级的要求,如上图:
    • DAG:(0,5)(5,4)(0,1)(0,6)(6,4)(6,9)(9,10)(9,11)(9,12)(11,12)(8,7)(7,6)(2,0)(2,3)(3,5)
    • Topo:8-7-2-3-0-5-1-6-4-9-10-11-12
    • DAG:(2,3)(0,6)(0,1)(2,0)(11,12)(9,12)(9,10)(9,11)(3,5)(8,7)(5,4)(0,5)(6,4)(6,9)(7,6)
    • Topo:8-7-2-3-0-6-9-10-11-12-1-5-4