Ch4 线性表/栈/队列

1. 线性表 List

顺序表

顺序表把表中元素定义为存储在数组的相邻元素中，其中curr称为”栅栏”，指向当前位置
实现
ArrayList.java
时间开销

操作元素			举例：insert 8
insert	Θ(n)	需右移curr后每个元素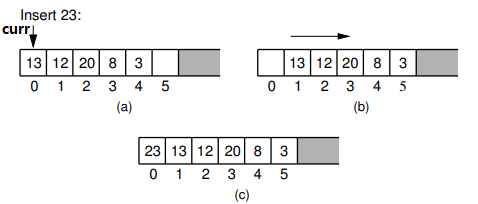
append	Θ(1)	已知当前长度，数组元素直接赋值
remove	Θ(n)	需左移curr后每个元素
操作栅栏
moveToStart/End/Pos	Θ(1)	直接重新赋值curr
prev/next	Θ(1)	直接重新赋值curr

单链表

链表基于指针，可以动态的为新元素分配**存储空间，它是由一系列节点（Link）对象组成的
实现
Link.java
LinkedList.java
时间开销**

操作元素			举例：insert 10
insert	Θ(1)	已知curr指针，插入link	** **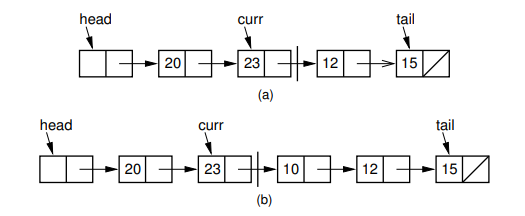
append	Θ(1)	已知tail指针，插入link
remove	Θ(1)	令curr.next = curr.next.next
操作栅栏			举例：remove 10
moveToStart/End	Θ(1)	curr指向head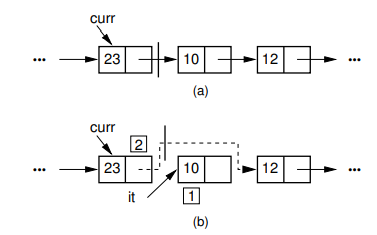
moveToPos	Θ(n)	curr从head开始移动
next	Θ(1)	curr.next
prev	Θ(n)	curr从head开始移动

🤷‍♂️AList对比LList

1. 空间效率：n为当前元素数，P为指针内存大小，E为数据大小，D为数组最大容量，则n满足如下条件时

1. 选择：调用next/prev多时选择AList；插入元素多，选择LList

   双链表

   为了弥补单链表对无法快速访问前结点的问题，我们重新构造Link，使其保存两个指针，分别指向前一个和后一个节点
   实现
   DLink.java
   DoubleLinkedList.java
   时间开销

操作元素			举例：insert 10，序号指示一系列赋值动作
insert	Θ(1)	需右移curr后每个元素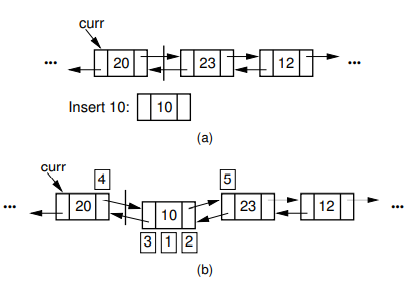
append	Θ(1)	已知当前长度，数组元素直接赋值
remove	Θ(1)	需左移curr后每个元素
操作栅栏
moveToStart/End/Pos	Θ(1)	直接重新赋值curr
prev/next	Θ(1)	直接重新赋值curr

2. 栈 Stack

栈是限定仅在一端进行插入或删除的线性表，元素一般都按照LIFO（后进先出）顺序

顺序栈

本质就是顺序**表(数组)的简化，建立栈时说明固定长度size，top表示栈顶，也是当前栈中元素数目
实现
AStack.java
时间开销**

操作栈			举例：push 8后满栈
push	Θ(1)	压入栈顶，即作为数组末尾元素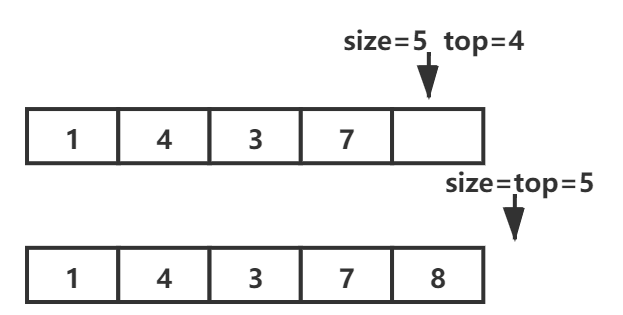
pop	Θ(1)	弹出栈顶，即删除数组末尾元素

链式栈

本质是对链表的简化，无需head结点，唯一需要top指针指向栈顶
实现
LStack.java
时间开销

操作栈			举例：push 7
push	Θ(1)	压入栈顶，即作为末尾Link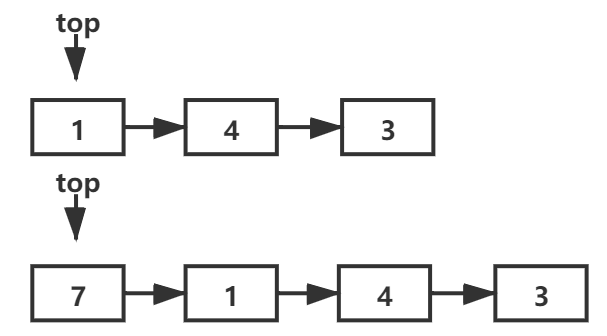
pop	Θ(1)	弹出栈顶，即删除末尾Link

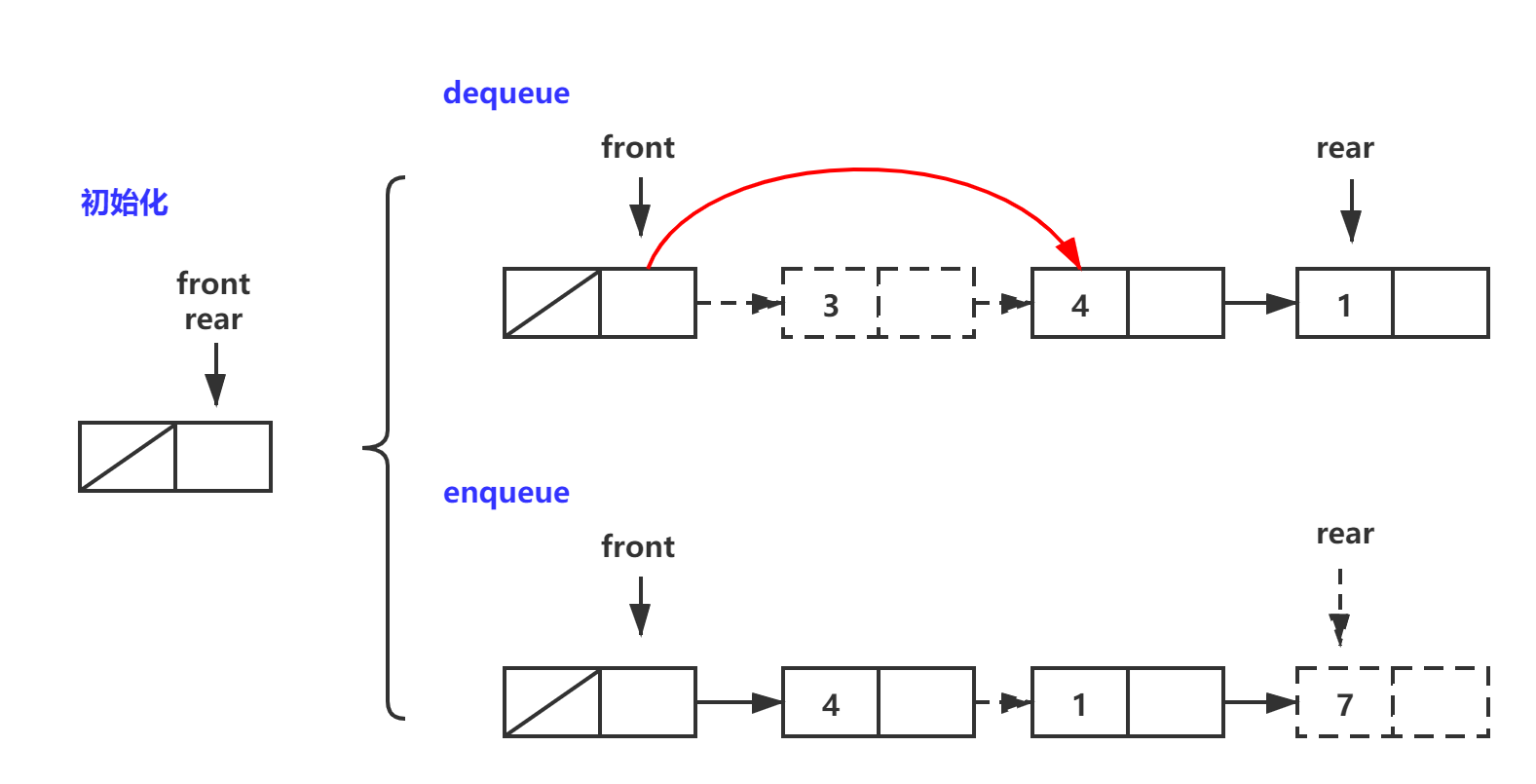
3. 队列 Queue

队列也是一类受限制线性表，元素只能从队尾插入(入队，enqueue)，从队首删除(出队，dequeue)，遵循FIFO先进先出原则.

顺序队列

基于顺序表(数组)，使用front和rear标记队首队尾，enqueue时插入元素rear右移dequeue时删除元素front右移.但是会产生“伪满”问题，即rear=size-1时无法插入新元素到数组中，但front由于dequeue实际上右移多位，即数组左侧实际依旧是空的.
时间开销

操作栈			举例：push 7
enqueue	Θ(1)	进入队尾,rear+1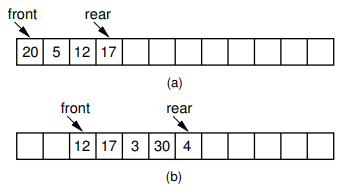
dequeue	Θ(1)	离开队首,front+1

循环队列

循环队列也是顺序队列，但假设顺序表为循环的，为此需使得一个元素始终为空，根据rear是否标记数组空元素分为两种实现：
(1)rear不指空
实现
AQueue.java

常用操作解释(开销同上顺序队列)		举例：尝试已满时入队
初始化	数组实际大小maxSize,可利用空间size=maxSize-1, 始终有一个位置为空,构造时令front=1,rear=0
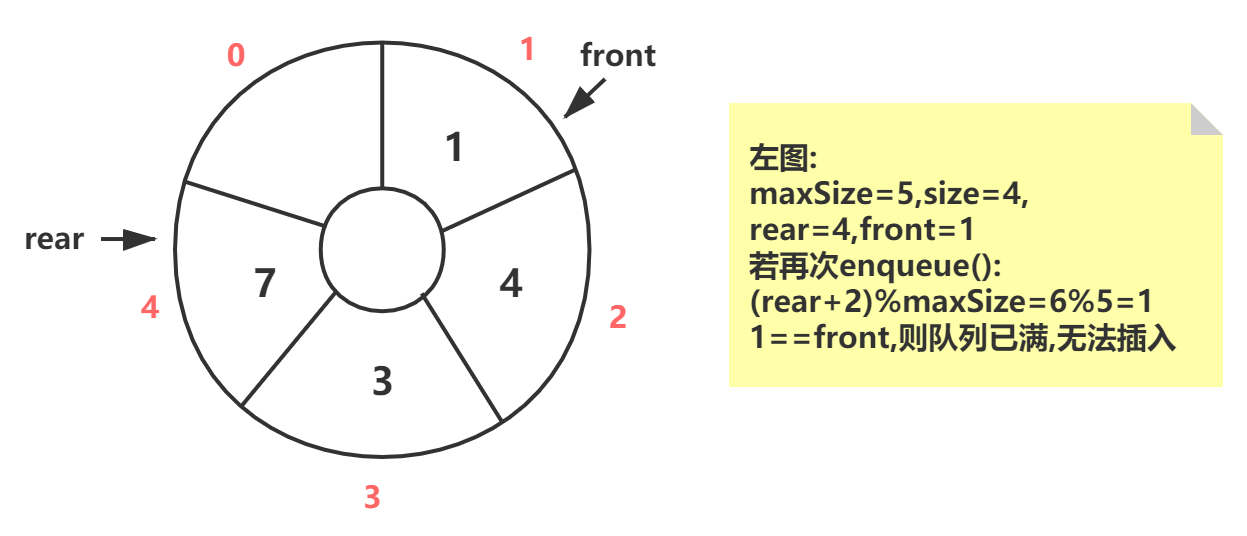判空	((rear + maxSize) - front + 1) % maxSize==0
判满	(rear+2)%maxSize==front
enqueue后	rear = (rear + 1) % maxSize
dequeue后	front = (front + 1) % maxSize

(2)rear不指空
实现略(基本一致)

常用操作解释(标红区别于上面情况)		举例：尝试已满时入队
初始化	数组实际大小maxSize,可利用空间size=maxSize-1, 始终有一个位置为空,构造时令front=0**,rear=0**
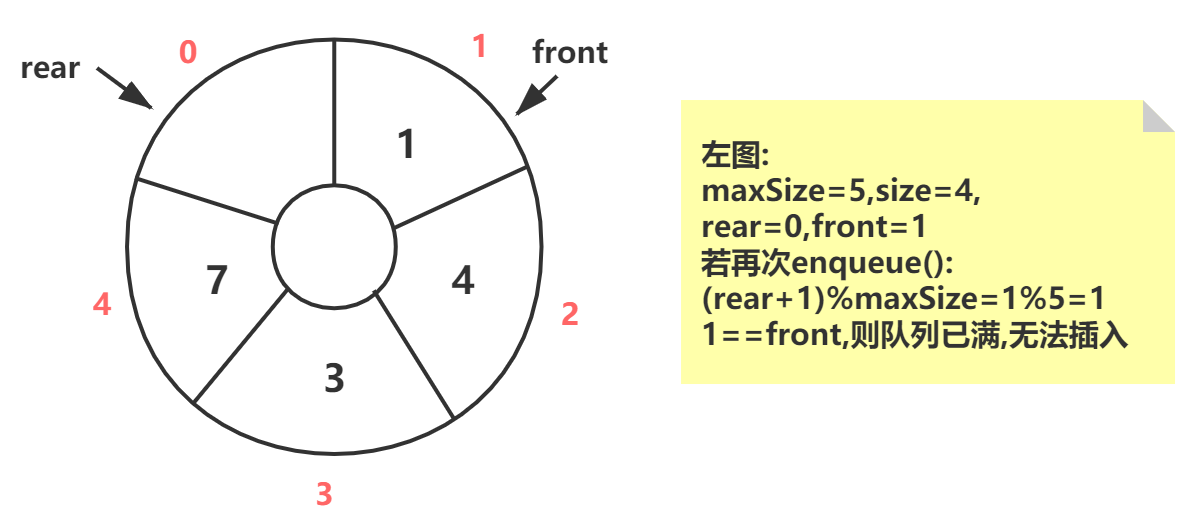判空	(rear - front + maxSize) % maxSize==0
判满	(rear+1)**%maxSize==front**
enqueue后	rear = (rear + 1) % maxSize
dequeue后	front = (front + 1) % maxSize

链式队列

实现
LQueue.java
链式队列基于链表，为了简便使用一个头节点.初始使得front与rear同时指向空头节点，之后front总是指向空头节点，rear总是指向尾节点