5.4 正则表达式

概述:正则表达式使用类似KMP中的抽象自动机来描述三种基本操作”连接,或,闭包”,由三种基本操作来描述”模式”,从而进行匹配

5.4.1 描述模式

  • 语言:字符串集合
  • 模式:语言的详细说明
  1. 连接操作: 当写出AB,即表示语言{AB},由AB连接而成
  2. 或操作:或预算”|”将两种选择包含在一种语言,A|B表示{A,B}
  3. 闭包操作:闭包允许模式的部分重复任意次数(含有0次),将”“放在模式后,A为{E,A,AA…}
    • 优先级:闭包>连接,AB*表示{A,AB,ABB…}
    • 空字符串E(Epsilon),存在于所有文本字符串
  4. 括号:用于改变优先级:(AB)*表示{E,AB,ABAB…}

5.4.2 缩略写法

  • 字符集描述符

regex1.png

  • 闭包简写

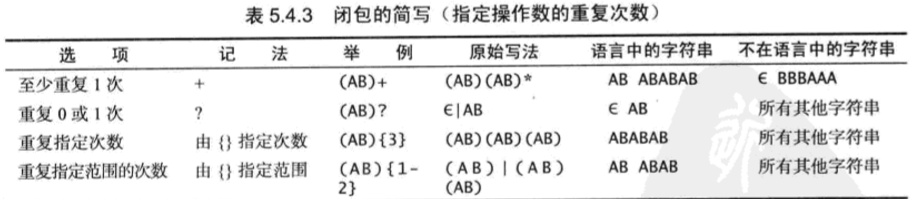
regex2.png

  • 应用

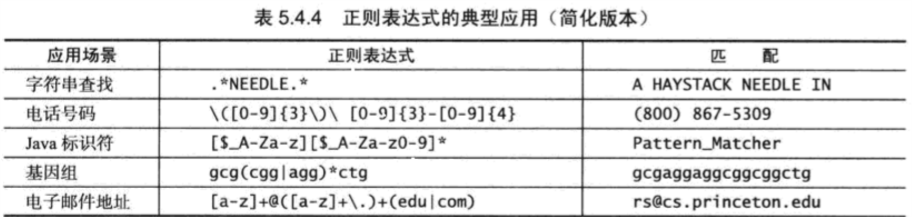
regex3.png

5.4.3 非确定优先状态自动机NFA

  • 因为或与闭包的存在,无法确定模式是否匹配,这是需要非确定自动,可以针对多种匹配可能猜出正确转换

5.4.4 NFA与DFA对比

  • NFA特点
    • 长M的regex每个字符在对于NFA中有且只有一个对应状态,起始为0,最终为接收状态
    • 字母表中字符对应状态都有出边,指向下一个字符状态(黑边)
    • 元字符”(,),|,*”对应状态至少一条出边(红边)可指向任意状态
    • 状态出边可能不只一条,但黑边(指向下个字符)只有一条
    • 约定所有模式都含在括号内
  • 不同
    • DFA字符是转换,NFA中字符是状态
    • DFA只需读取txt中部分字符就能抵达停止状态,NFA需要一直读取到文本结束判断是否到接收状态
  • 转换
    • 匹配转换:当前状态字符和文本字符匹配,则由黑边进入下一状态
    • E转换:自动机通过红边进入下一状态而无需接收字符,即与空字符串E匹配

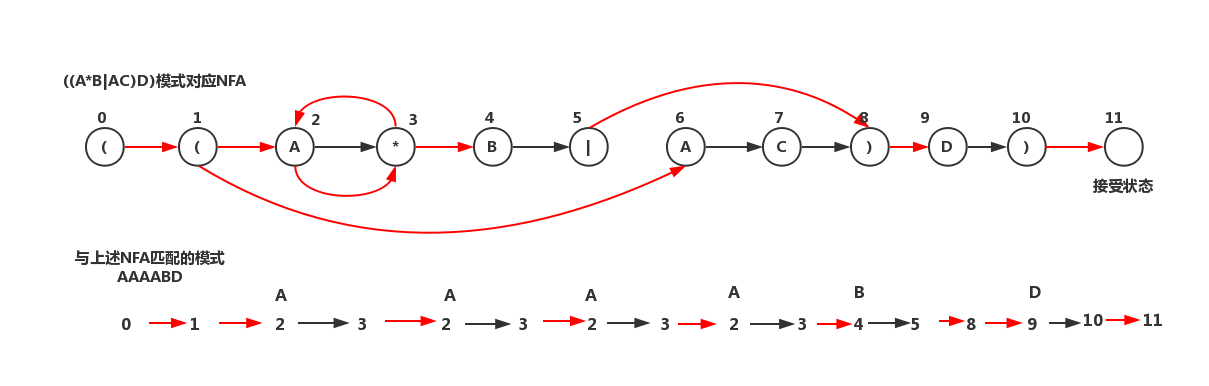
NFA1.png

5.4.5 模拟NFA运行

  1. 自动机表示
    • 表达式本身和匹配转换:char[] re,当re[i]存在,则存在i到i+1匹配转换
    • E转换: 有向图G,红边即连接两顶点的有向边
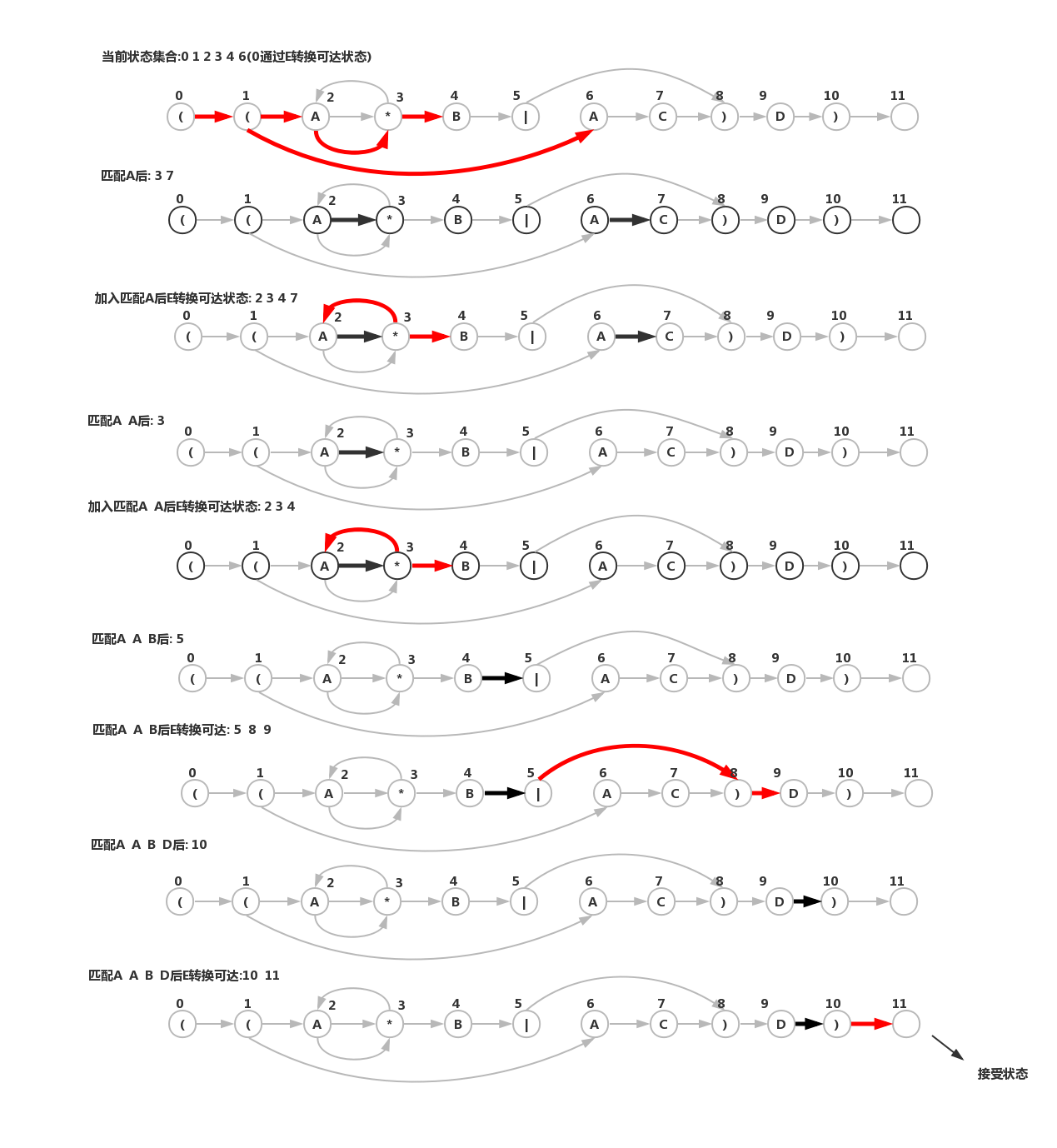
  2. NFA模拟和可达性
    • 初始化:查找0状态通过E转换可达的所有状态初始化集合
    • 检查匹配: 对集合每个状态检查是够与第一个字符匹配,检查完毕,则得到与第一个字符匹配的状态集合
    • 依次输入其余字符,重复以上步骤,直到读取完毕
    • 最终结果
      • 状态集合有接受状态:匹配成功
      • 不含接受状态:匹配不存在
  • 对((A*B|AC)D)的NFA输入AABD模拟

NFA2.png

  1. //NFA模拟
  2.     public boolean recognizes(String txt){
  3.         Bag<Integer> pc = new Bag<>();
  4.         DirectedDFS dfs = new DirectedDFS(G,0);//有向图多点可达性,0开始的E转换
  5.         for (int v = 0; v < G.V(); v++)
  6.             if (dfs.marked(v)) pc.add(v);//初始化
  7.         for (int i = 0; i < txt.length(); i++){
  8.             Bag<Integer> match = new Bag<>();//匹配状态集合
  9.             for (int v: pc) {
  10.                 if (v < M)//txt未读取完毕
  11.                     if (re[v] == txt.charAt(i) || re[v] == '.')//匹配或通配
  12.                         match.add(v + 1);
  13.             }
  14.             pc = new Bag<>();
  15.             dfs = new DirectedDFS(G,match);//用当前状态集合重建dfs
  16.             for (int v = 0; v < G.V(); v++)
  17.                 if (dfs.marked(v)) pc.add(v);
  18.         }
  19.         for (int v: pc) if (v == M) return true;//最终集合有接受状态
  20.         return false;
  21.     }

算法分析

  • 模拟长M的regex是否可识别长N的txt,最坏情况下颌MN成正比

证明:对txt中每个字符,会便利一个大小不超过M的集合并在E转换有向图中深度优先搜索,且图中边数不会超过2M

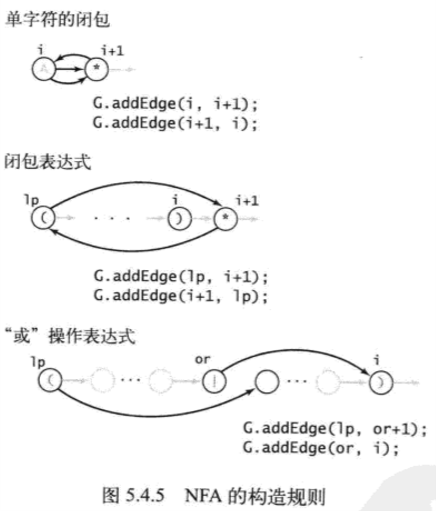
5.4.6 构造NFA

  • 连接:无需其余处理,匹配转换就是连接关系
  • 括号:将regex中左括号索引入栈,遇到右括号时,左括号弹出
  • 闭包操作
    • 单个字符后:在字符和状态间添加两条相互指向的E转换
    • 右括号后:在对应左括号和间添加相互执行的E转换
  • 或操作:如(A|B),添加两条E转换
    • 左括号指向B中第一个字符
    • |指向右括号
    • 将(和|都压入栈中,遇到)时所需的(和|都会在栈顶,分别对应不同匹配

NFA3.png

  1. public class NFA {
  2.     private char[] re;//regex本身/匹配转换
  3.     private Digraph G;//epsilon转换
  4.     private int M;//状态数量
  6.     //NFA构造
  7.     public NFA(String regexp){
  8.         Stack<Integer> ops = new Stack<>();
  9.         re = regexp.toCharArray();//String转换为char[]
  10.         M = re.length;
  11.         G = new Digraph(M+1);
  13.         for (int i = 0; i < M; i++){
  14.             int lp = i;
  15.             if (re[i] == '(' || re[i] == '|') ops.push(i);//压入(和|
  16.             else if (re[i] == ')')//右括号
  17.             {
  18.                 int or = ops.pop();
  19.                 if (re[or] == '|'){//若弹出|
  20.                     lp = ops.pop();//继续弹出(
  21.                     G.addEdge(lp, or+1);//左括号->|后第一个字符
  22.                     G.addEdge(or, i);//|->右括号
  23.                 }
  24.                 else lp = or;//无|,则只弹出(
  25.             }
  26.             //括号处理在闭包处理之前,否则lp的值总是i
  27.             if (i < M-1 && re[i+1] == '*'){//闭包处理
  28.                 G.addEdge(lp, i+1);
  29.                 G.addEdge(i+1, lp);
  30.             }
  31.             if (re[i] == '(' || re[i] == '*' || re[i] == ')')//添加(,),*后的E转换
  32.                 G.addEdge(i, i+1);
  33.         }
  34.     }
  36.     //NFA模拟
  37.     public boolean recognizes(String txt){}
  38. }

算法分析

  • 构造长度M的regex对应NFA所需时间空间在最坏情况下和M成正比

证明:对regex中每个字符,最多添加三条E转换(*),且可能执行一到两次栈操作

  • 一般用例

NFA4.png