2.4.4.7/Ex2_2_33/34 索引优先队列

很多时候,数据输入流有多个,且数量巨大(10亿个),使用索引可以确定不同输入流,使用优先队列可以确保无论输入多长都可以读入并排序,二者结合即索引优先队列

  1. import edu.princeton.cs.algs4.In;
  2. import edu.princeton.cs.algs4.StdOut;
  4.     /*
  5.    本例使用merge(),基于索引优先队列,将作为命令行输入的多
  6.    行字符串(字符串本身升序排好),归并为为一行有序的输出.
  7.     */
  9. public class IndexMinPQ<Key extends Comparable<Key>> {
  10.     private Key[] keys;//存放原始数据,顺序不变
  11.     private int[] pq;//存放索引的二叉堆,从1开始
  12.     private int[] qp;//存放索引的逆序,qp[pq[i]] = pq[pq[i]] = i;
  13.     private int N;//PQ中元素数量
  15.     /*
  16.     ----------constructor and Helpers-----------
  17.      */
  19.     public IndexMinPQ(int maxN){
  20.         keys = (Key[]) new Comparable[maxN+1];
  21.         pq = new int[maxN+1];
  22.         qp = new int[maxN+1];
  23.         //当索引i不在队列中,令qp[i] = -1
  24.         for (int i =0; i<= maxN; i++) qp[i] = -1;
  25.     }
  27.     public boolean isEmpty(){ return N == 0;}
  28.     public int size(){ return N;}
  29.     //通过返回对索引的查找结果确定是否包含元素
  30.     public boolean contains(int k){ return qp[k] != -1; }
  32.     /*
  33.     ----------major function-----------
  34.      */
  36.     public void insert(int pri, Key key){
  37.         N++;
  38.         pq[N] = pri;//保存索引
  39.         qp[pri] = N;//保存pq的逆序
  40.         keys[pri] = key;
  41.         swim(N);
  42.     }
  44.     public Key min(){ return keys[pq[1]]; }
  46.     public int delMin(){
  47.         int indexOfMin = pq[1];
  48.         exch(1, N--);
  49.         sink(1);
  50.         keys[pq[N+1]] = null;
  51.         qp[pq[N+1]] = -1;
  52.         return indexOfMin;//返回indexOfMin,确定输入流
  53.     }
  55.     private void change(int pri, Comparable key){
  56.         keys[pri] = key;
  57.         int index = qp[pri];
  58.         swim(index);
  59.         sink(index);
  60.     }
  62.     public void delete(int pri){
  63.         int index = qp[pri];
  64.         exch(index, N--);
  65.         swim(index);
  66.         sink(index);
  67.         keys[pri] = null;
  68.         qp[pri] = -1;
  69.     }
  71.     //此处使用large(),构造小顶堆
  72.     private boolean larger(int i, int j){
  73.         return keys[pq[i]].compareTo(keys[pq[j]]) > 0;
  74.     }
  75.     private void exch(int i, int j){
  76.         int swap = pq[i];
  77.         pq[i] = pq[j];
  78.         pq[j] = swap;
  80.         qp[pq[i]] = i;
  81.         qp[pq[j]] = j;
  82.     }
  84.     public void swim(int k){
  85.         while (k > 1 && larger(k/2, k)){
  86.             exch(k/2, k);
  87.             k = k/2;
  88.         }
  89.     }
  91.     public void sink(int k) {
  92.         while (k * 2 <= N) {
  93.             int j = k * 2;
  94.             if (larger(j, j + 1) && j < N) j++;//取子结点较大者;j<N,取等号j++溢出
  95.             if (!larger(k, j)) break;//比较父子大小
  96.             exch(k, j);
  97.             k = j;
  98.         }
  99.     }
  101.     public static void merge(In[] streams){
  102.         int N = streams.length;
  103.         IndexMinPQ<String> pq = new IndexMinPQ<>(N);
  105.         for (int i = 0; i < N; i++)
  106.             if (! streams[i].isEmpty())
  107.                 pq.insert(i,streams[i].readString());
  110.         while (!pq.isEmpty()){
  111.             StdOut.println(pq.min());
  112.             int i = pq.delMin();
  114.             if (! streams[i].isEmpty())
  115.                 pq.insert(i,streams[i].readString());
  116.         }
  117.     }
  119.     /*
  120.     -----------test function-----------
  121.      */
  123.     public static void main(String[] args){
  124.         int N = args.length;
  125.         In[] streams = new In[N];
  126.         for (int i = 0; i < N; i++)
  127.             streams[i] = new In(args[i]);
  128.         merge(streams);
  129.     }
  130. }

算法理解:

关于索引优先队列:

在一般的优先队列中,我们只能通过delMax()访问最大元素,无法直接访问队列中其他元素进行更新或删除,要是建立一个映射关系,让队列中第k个元素操纵着原始数据,队列中针对这种关系排序即可,不改变原始数据结构.实现这种映射控制需要索引(priority)

上述算法中,keys[]即为原始数据结构,只有change()或delete()会改变其中元素,排序对其无影响;pq[]为索引队列,里面依据keys[]中元素堆有序保存了对应的索引,pq[1]即保存了最小元素的索引,比如pq[1]=3,说明keys[3]的元素最小

当要更新元素时,如将keys[5]元素改变,再去维护pq[i]的值,但除非遍历pq[],无法获悉哪个元素pq[i]保存了5,因此必须再添加一个数组,保存与对象相关的队列数组元素下标,qp[pq[i]]=pq[qp[i]]=i;,假如qp[5] = 3,则pq[3]中保存了索引5,这时恢复pq有序,对应恢复qp有序.

关于归并输入流:

假设命令行参数传入m1.txt,m2.txt,m3.txt三个文件,每个文件中有一列升序的字符串,则main函数stream[]是含有N=3的数组,则merge()一开始读取stream[]三个流元素的首个字符串,三个字符串构成索引优先队列,然后delMin(),输出并删除三者最小,再补充删去元素索引对应的下个字符串,知道所有流下的所有字符串都被输出并删除,达成归并不同流并排序的目的.

图示:

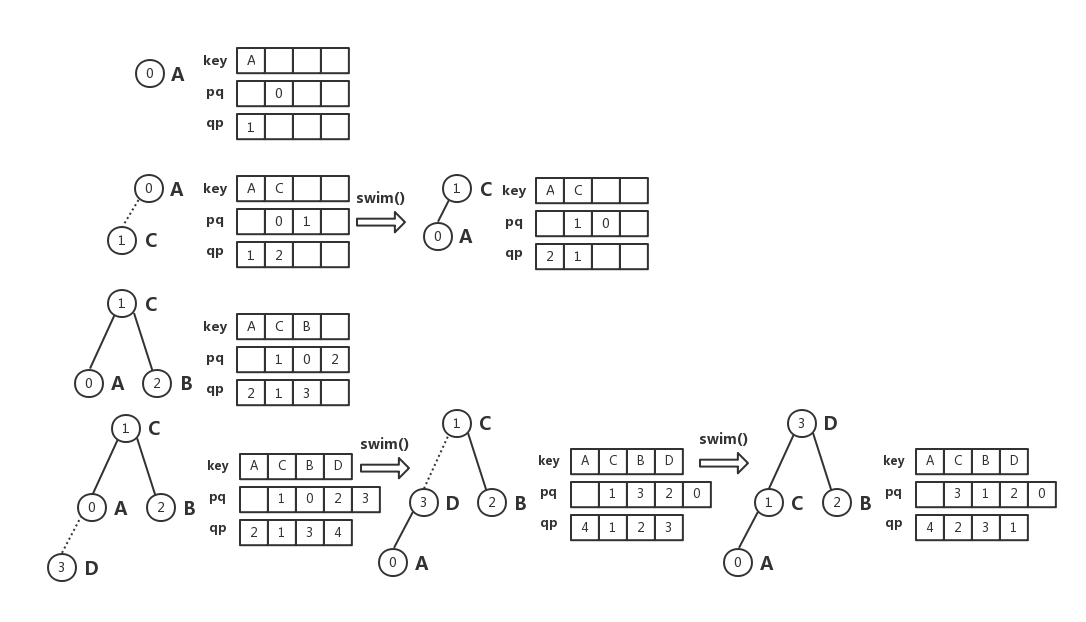
索引优先队列.jpg

算法分析:

大小N的索引优先队列,插入insert(),改变优先级change(),删除delete(),删除最小元素delMin()操作所需比较次数和logN成正比

证明:由堆中所有路径最长为~lgN,可得

N个元素的堆索引优先队列不同操作最坏情况下成本

操作 比较次数增长级
insert() logN
change() logN
contains() 1
delete() logN
min() 1
minIndex() 1
delMin() logN

Review:

  1. 索引pri是指定key[]中的某个位置,实际元素即key[pri],pq[i]==pri代表此索引堆有序后在堆中第i处,为方便找出key[pri]的索引在pq[]哪个位置,引入qp[],使得qp[pri]=qp[pq[i]]=i;
  2. sink()中if (larger(j, j+1) && j < N) j++构造小顶堆找子结点较小者,构造大顶堆找子结点较大者
  3. 三个边界取等问题
  • 构造函数for (int i=0; i <= maxN; i++),因为contains通过qp[pri]是否为-1判断,qp[maxN]即保存key[maxN]的索引倒序
  • swim()while (k > 1 && larger(k/2, k)),若k>=1,k=1时操作空元素pq[0]
  • sink()while (k*2 <= N),当k恰为2次幂时,层数加一,需要判断下沉.
  1. insert()在末尾操作只需swim(),change()和delete()涉及中间操作要先swim()在sink()
  2. merge()实现不唯一
  1. private static void merge(In[] streams){
  2.         int N = streams.length;
  3.         IndexMinPQ pq = new IndexMinPQ(N);
  5.         //读入初始三个值
  6.         for (int i = 0; i < N; i++)
  7.             if (! streams[i].isEmpty())
  8.                 pq.insert(streams[i].readString(), i);
  11.         StdOut.println(pq.showMin());
  12.         int i = pq.delMin();
  14.         while (!streams[i].isEmpty()){
  15.             pq.insert(streams[i].readString(), i);
  17.             StdOut.println(pq.showMin());
  18.             i = pq.delMin();
  19.         }
  20.     }