Ch4 随机变量的数字特征

前三章主要关注随机变量及其统计规律性,本章关注随机变量本身的数字特征.
描述随机变量的数字特征有数学期望,方差,矩;描述二维随机变量(X,Y)中XY关系的有协方差和相关系数

1. 数学期望

以概率为权的加权平均值称为随机变量的数学期望

1.1 离散型

1.2 连续型

:::info 个人理解:对于连续随机变量,上式即为概率/权值,因此”权×随机变量取值x”后在(-∞,+∞)上积分即得到连续离散变量的期望 :::

1.3 随机变量函数

:::info 同理,是随机变量的概率分布函数,再乘随机变量函数值得到期望 :::

1.4 期望性质

1. ,常数的期望是它本身
2. 
3. 
4. 当X与Y相互独立时

2. 方差

方差用来描述随机变量X的取值在期望E(X)周围集中的程度,本质是一个随机变量函数的期望

2.1 离散型

2.2 连续型

在实际计算中一般使用

2.3 方差性质

1. 
2. 
3. 当XY独立时

**小结常见分布的期望与方差

	分布	期望	方差
离散
连续

3. 变异系数,原点矩,中心距

3.1 变异系数

D(x)衡量了X取值在E(X)周围的集中程度,但D(X)会受到量纲的影响,比如同一组数据以cm标注的身高D(X)一定大于以m标注的,此时考虑变异系数

变异系数衡量了X取值在E(X)周围的相对集中程度,可以理解为分子标准差和分母期望同时上下约去单位

3.2 原点矩和中心矩

期望和方差和推广为X的原点矩和中心矩

:::info 可以发现期望就是一阶原点矩,方差就是二阶中心距(一阶中心距为0)
原点矩:因为,相对于原点来说
中心距:因为,以E(X)为中心 :::

4. 协方差和相关系数

4.1 协方差

对于二维随机变量(X,Y)我们使用协方差描述X和Y的关系

协方差性质

协方差矩阵
(X,Y)的协方差矩阵

扩展

4.2 相关系数

类似于D(X)被量纲影响所以引入变异系数,协方差同样受量纲影响,为此引入相关系数
首先需要标准化随机变量X,Y

性质

1. 
2. ,常用于计算R(X,Y)

意义
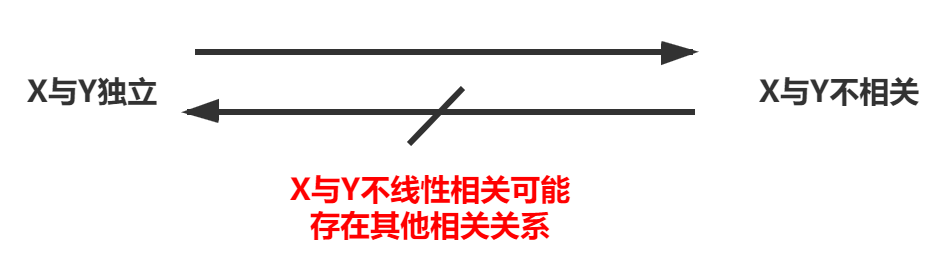
:::info 不相关和独立性是两个概念:不相关专门指不线性相关,但此时可存在其他相关关系,则XY就不独立
:::