Knuth-Morris-Pratt子字符串查找

算法描述

  • KMP算法基本思想是匹配失败时,已经知晓部分文本,从而避免回退到所有字符前

DFA模拟

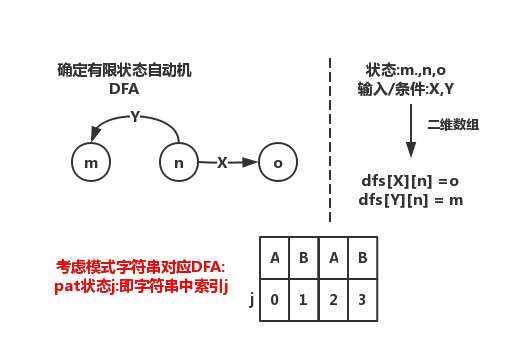
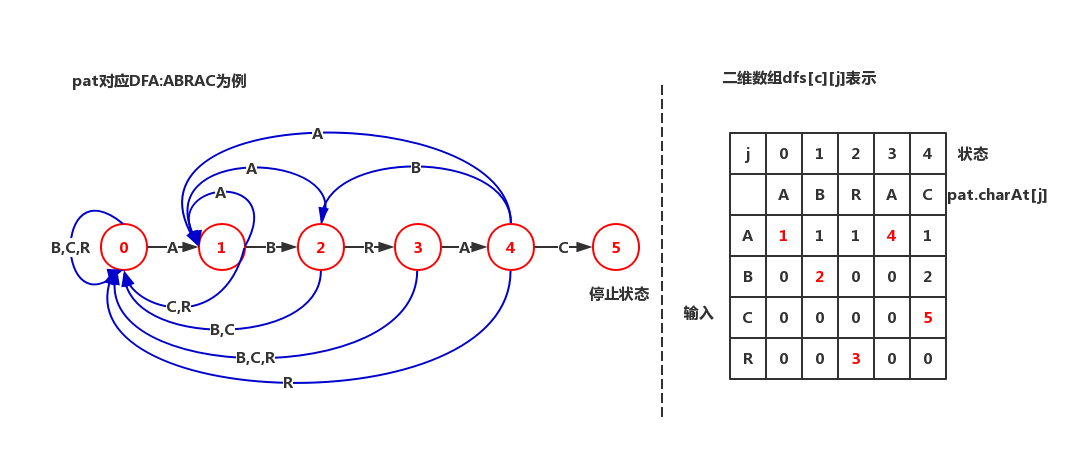
DFA确定优先有限状态自动机,由状态和转换构成,pat中的每一个字符可代表一个状态

二维数组表示:dfa[转换][状态]即为一个DFA 字符串查找:DFA中,只有一条是匹配转换,从j->j+1,其余都非匹配,回到之前某个状态

DFA.png
DFA1.png

KMP算法和DFA

  • 模拟DFA运行:只要知道dfa[][]就可以得到KMP算法:当txt的i和pat的j指向字符匹配失败(从txt的i-j+1开始匹配),pat的下一可能匹配位置应从i-dfa[txt.charAt(i)][j]开始,但从该位置开始的dfa[txt.charAt(i)][j]个字符和pat的前dfa[txt.charAt(i)][j]个字符相同,无需回退指针i,只需将j设置为dfa[txt.char(i)][j]并且i+1即可
  1. //模拟DFA运行
  2. public int search(String txt){
  3.     int i,j,N = txt.length(), M = pat.length();
  4.     for (i = 0, j = 0; i < N && j < M; i++)
  5.         j = dfa[txt.charAt(i)][j];
  6.     if (j == M) return i-M;//找到匹配
  7.     else return M;//未找到匹配
  8. }

构造DFA

  • 核心:dfa[i][j]要理解为j状态时接收i时发生的转换
  • 考虑暴力解法在pat.charAt(j)匹配失败时
    • 回退文本指针i至初始位置
    • 文本指针右移一位,重新开始扫描
    • 重点在于:pat.charAt(1)到pat.charAt(j-1)被重新扫描,首字母和最后一个字符忽略

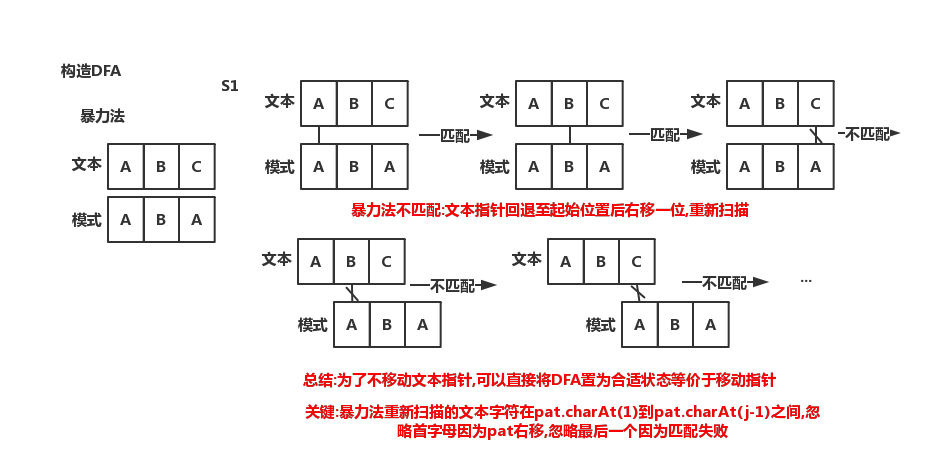
con1.png

  • 考虑DFA只要知道暴力法回退扫描完后DFA的状态,将其重置为此状态,就达到了不移动指针但等价的效果
    • 匹配失败:dfa[][X]复制到dfa[][j]
    • 匹配成功: dfa[pat.charAt(j)][j]设置为j+1
    • 重启状态X: X = dfa[pat.charAt(j)][X]

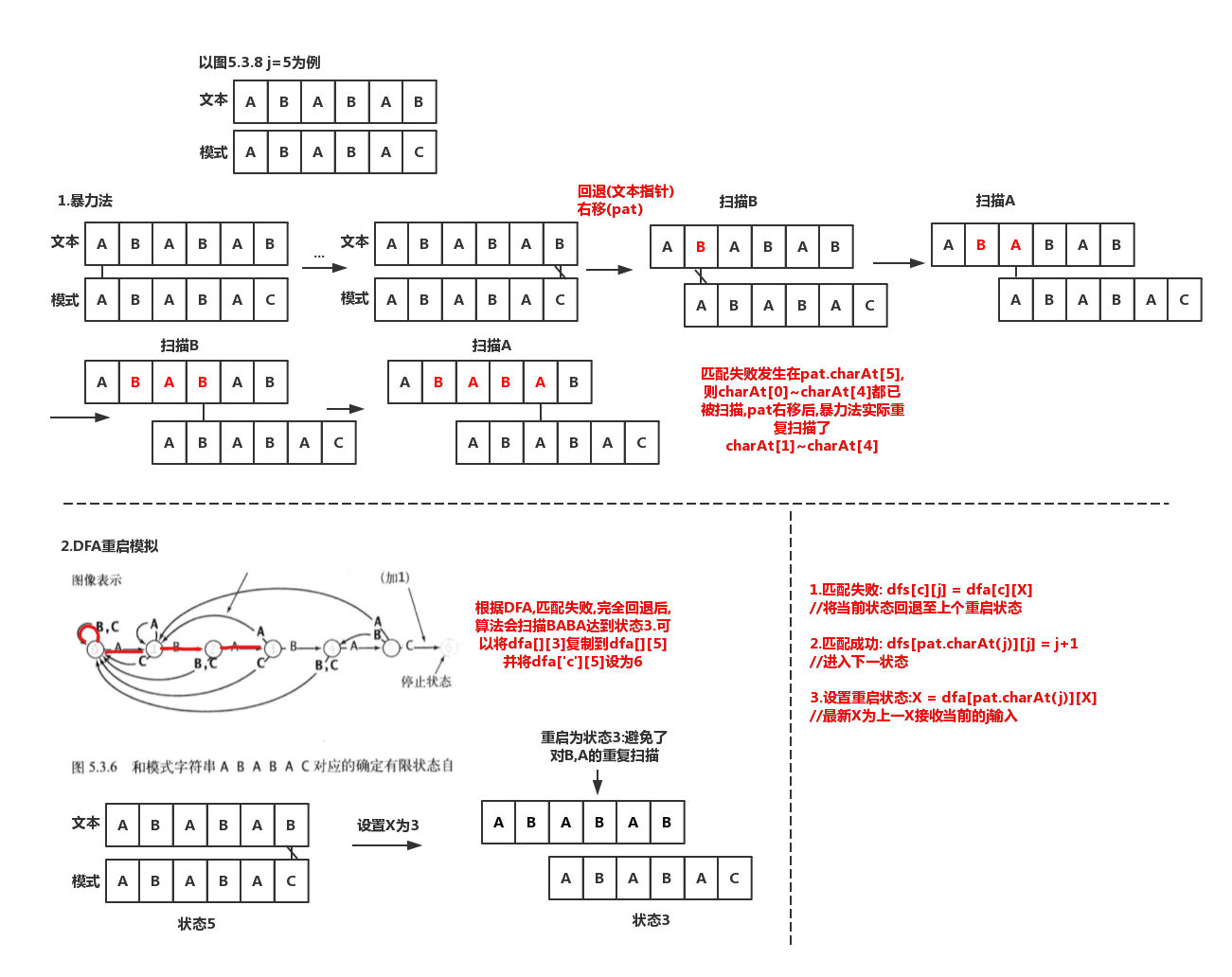
con2.png

  1. public KMP(String pat){
  2.     this.pat = pat;
  3.     int M = pat.length();
  4.     int R = 256;
  5.     dfa = new int[R][M];
  6.     //构建DFA
  7.     dfa[pat.charAt(0)][0] = 1;
  8.     for (int X = 0, j = 1; j< M; j++){
  9.         for (int c = 0; c < R; c++)
  10.             dfa[c][j] = dfa[c][X];//匹配失败
  11.         dfa[pat.charAt(j)][j] = j+1;//匹配成功
  12.         X = dfa[pat.charAt(j)][X];//更新重启状态
  13.     }
  14. }

KMP算法API

返回类型 方法 描述
KMP(String pat) 根据pat构建DFA
int search 输入txt运行DFA 
  1. public class KMP {
  2.     private String pat;
  3.     private int[][] dfa;
  4.     public KMP(String pat){}
  5.     public int search(String txt){}
  7.     public static void main(String[] args){
  8.         String pat = args[0];
  9.         String txt = args[1];
  10.         KMP kmp = new KMP(pat);
  11.         StdOut.println("text:   " + txt);
  12.         int offset = kmp.search(txt);
  13.         StdOut.print("pattern");
  14.         for (int i = 0; i < offset; i++)
  15.             StdOut.print("  ");
  16.         StdOut.println(pat);
  17.     }
  18. }

算法分析

  • 长度M的pat和N的txt,KMP算法访问字符不会超过M+N个

证明:在KMP()构造DFA时访问pat中每个字符一次,在search()访问每个txt字符一次