3.3 平衡查找树

3.2 二叉查找树(见算法3.3)

3.3 平衡查找树

3.3.1 2-3查找树

定义:2-3查找树为一棵空树或由以下结点构成:

• 2-结点:含有一个键和两个指针,左链2-3子树键值都小于该结点,右链都大于
• 3-结点:含有两个键和三个指针,左链2-3子树键值小于该结点,中链键值介于该结点两个键之间,右链键值都大于该结点

3.3.1.1 查找

2-3查找树的查找和二叉查找树类似,根据键值大小进入子树递归查询,若无结果,返回NULL

3.3.1.2 插入

• 二叉树插入时,先进行查找,若命中key则更新val,否则return一个新结点挂在树的底部.但2-3查找树的插入分为5种操作
  • 向2-结点插入新键

如果查找结束于一个2-结点,此时只需把2-结点替换为3-结点,将新键按照左小右大放置

• 向一棵只含有一个3-结点的树(子树)插入新键

此时先临时把新键存入该结点中,使之成为4-结点:含有3个键和4个指针,然后将其转化为3个2-结点,取三个键的中间值作为父结点,剩余两个作左右结点

• 向一个父结点为2-结点的3-结点插入新键

同样构造临时4-结点,然后取出中间值,移动到父结点中,剩余两个值拆开作为父结点的子结点

• 向一个父结点为3-结点的3-结点插入新键

构造临时4-结点,然后取出中间值,移动到父结点中,父结点此时也成为4-结点,则取出中间值作为父2-结点,拆分其余两值作为子结点

• 分解根节点
  如果遇到某结点到根结点路径上全是3-结点,那根结点最终会成为4-结点,同理拆分为三个2-结点,树高加一

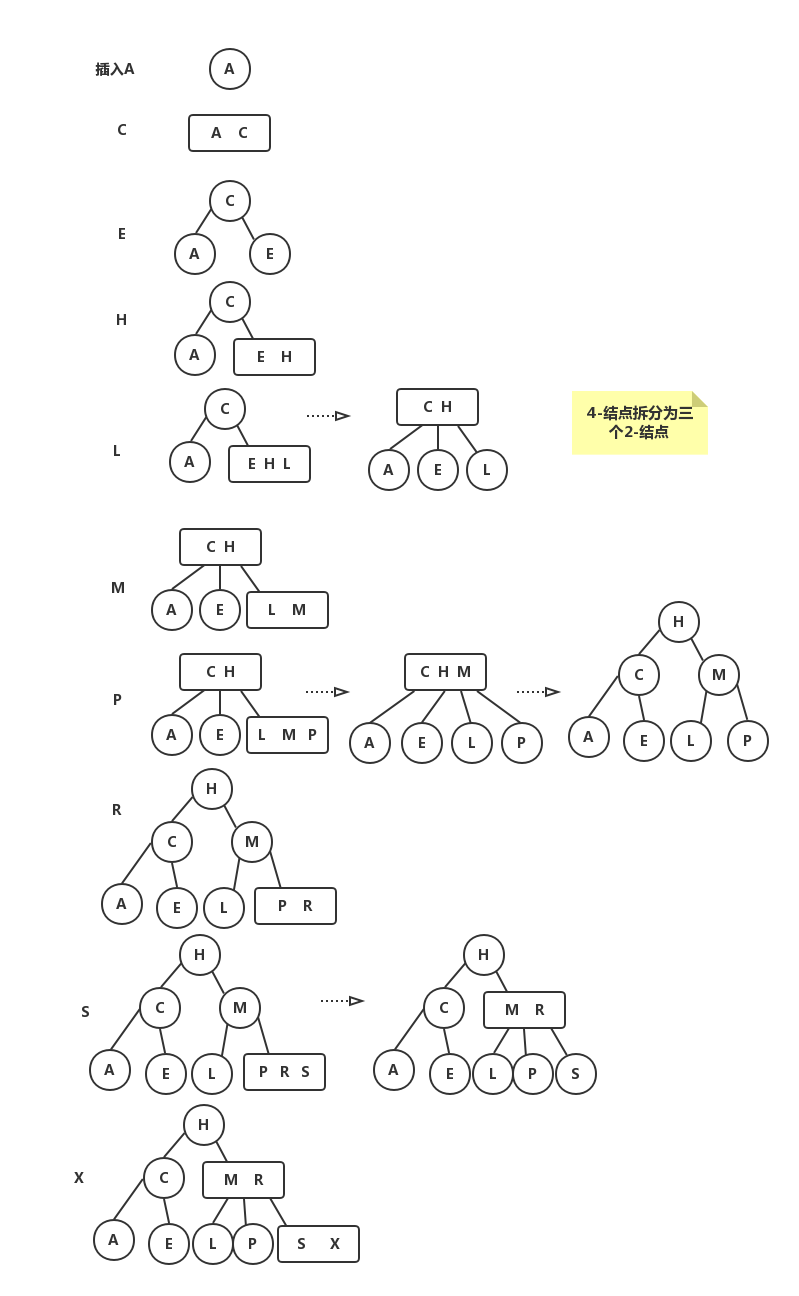
3.3.1.7 局部变换

• 2-3树插入算法的根本在于这些变化是局部的:除了相关的结点和链接之外不必修改或检查树的其他部分

3.3.1.8 全局性质

• 2-3树算法的局部变换不会影响数的全局有序性和平衡性:任意空链接到根结点的路径长度都是相等的
• 和二叉树比较:二叉树是自上而下生长,但2-3树是由下向上生长

算法分析

2-3树主要关注最坏情况下的性能,因为符号表实现中,一般无法控制用例的输入,对最坏情况的分析才能保证性能

在一棵大小N的2-3树中,查找和插入操作访问的结点不超过lgN个

证明:一棵含有N个结点的2-3树高度在logN(全是3-结点)到lgN之间(全是2-结点)