1. 图
图是由一组顶点和一组可连接两个顶点的边组成的数据结构,根据边是否有指向或者是否带有权值可分为:
- 无向图:只由一组顶点和一组可连接两个顶点的边构成(a)
- 有向图:边是单向的,每条边连接的两个顶点是一个有序对(b)
- 加权有向图:除了有向图性质,其每条边还带有权重(c)
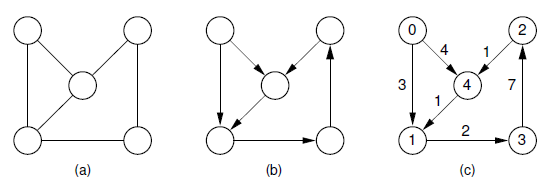
2. 图的实现
API
下列API构成后续一系列图算法的基础GraphADT.java
| 方法 | 解释 |
|---|---|
| int n() | 返回图顶点数n |
| int e() | 返回图边数e |
| int first(int i) | 返回顶点i的第一个邻接点索引,无结果时返回n |
| int next(int i, int j__) | 返回顶点i的下一邻接点索引,无结果时返回n |
| void setEdge(int i, int j, int weight__) | 创建边i-j,设权重为weight |
| void delEdge(int i, int j, int weight) | 删除边i-j |
| int weight(int i,int j__) | 返回边i-j的权重 |
| int getMark(int i__) | 返回顶点i在数组Mark中的信息(见邻接矩阵实现) |
| int setMark(int i, int val) | 设置顶点i在数组Mark中的信息 |
邻接矩阵实现(Adjacency Matrix)
Edge.java
Graphm.java
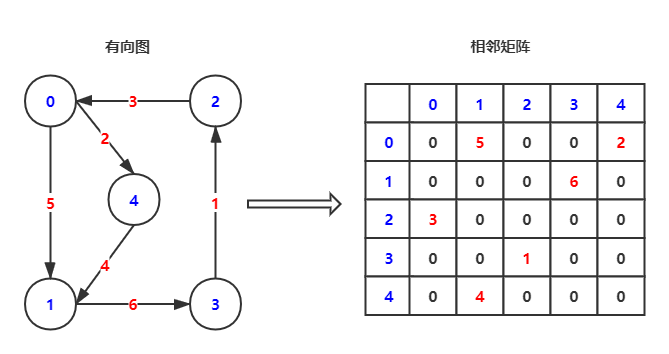
邻接矩阵实现中有几个数据结构
- int[][] matrix:边矩阵:matrix[1][2]中存储着顶点1到顶点2边的权重,当两点之间无边连接时权值为0
- int[] Mark:Mark数组,存放顶点v的邻接点:Mark[2]存放顶点2的邻接点
|
 | 执行 | 结果 |
| —- | :—-: | :—-: |
| | i=e() | i=6 |
| | i=n() | i=5 |
| | i=first(1) | i=3 |
| | i=next(1,3) | i=5(点1无其他邻接点,返回n=5) |
| | i=next(0,1) | i=4(点0的下一邻接点为4) |
| | i=weight(2,4) | i=0(不存在边2-4,权值为0) |
| 执行 | 结果 |
| —- | :—-: | :—-: |
| | i=e() | i=6 |
| | i=n() | i=5 |
| | i=first(1) | i=3 |
| | i=next(1,3) | i=5(点1无其他邻接点,返回n=5) |
| | i=next(0,1) | i=4(点0的下一邻接点为4) |
| | i=weight(2,4) | i=0(不存在边2-4,权值为0) |
邻接表实现(Adjacency List)
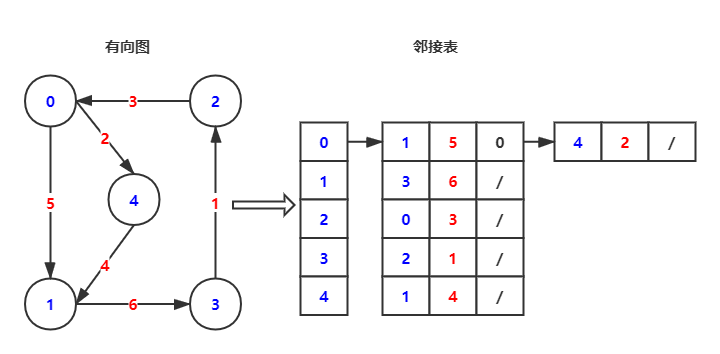 |
执行 | 结果 |
|---|---|---|
| i=e() | i=6 | |
| i=n() | i=5 | |
| i=first(1) | i=3 | |
| i=next(1,3) | i=5(点1无其他相邻点,返回n=5) | |
| i=next(0,1) | i=4(点0的下一相邻点为4) | |
| i=weight(2,4) | i=0(不存在边2-4,权值为0) |
:::danger 上例都以有向图说明,实际上这两种实现广泛适用于实现各类图结构 :::
3. 图的遍历
:::info
- DFS实现:使用递归/隐式栈
-
DFS
下方递归方法实现了有向图的DFS,其中Pre/PostVisit可以是打印操作等行为:
在for循环前打印V,可实现**先根遍历**
- 在for循环后打印V,可实现**后根遍历**
/** Depth first search */static void DFS(Graph G, int v) {PreVisit(G, v); // Take appropriate actionG.setMark(v, VISITED);for (int w = G.first(v); w < G.n() ; w = G.next(v, w))if (G.getMark(w) == UNVISITED)DFS(G, w);PostVisit(G, v); // Take appropriate action}
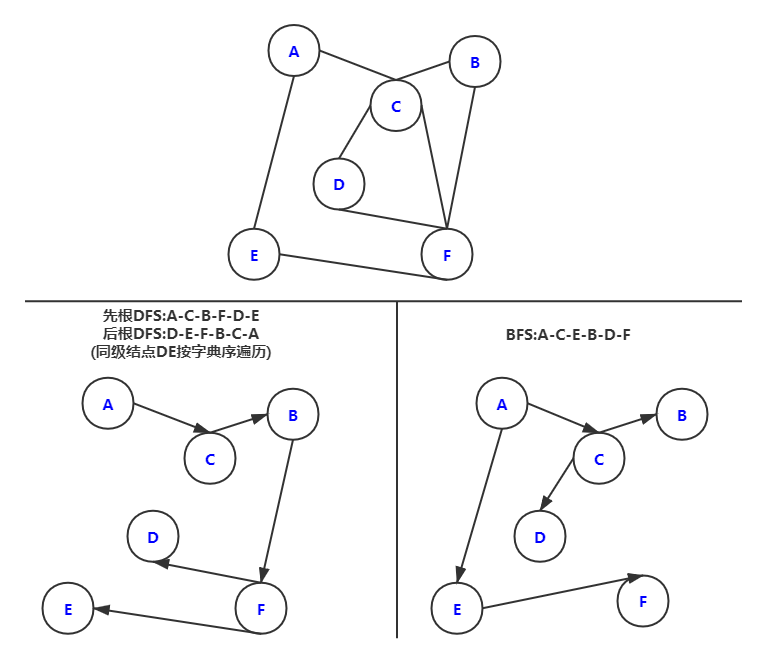
BFS
:::info 举例:给定无向图,求DFS和BFS结果/** Breadth first (queue-based) search */static void BFS(Graph G, int start) {Queue<Integer> Q = new AQueue<Integer>(G.n());Q.enqueue(start);G.setMark(start, VISITED);while (Q.length() > 0) { // Process each vertex on Qint v = Q.dequeue();PreVisit(G, v); // Take appropriate actionfor (int w = G.first(v); w < G.n(); w = G.next(v, w))if (G.getMark(w) == UNVISITED) { // Put neighbors on QG.setMark(w, VISITED);Q.enqueue(w);}PostVisit(G, v); // Take appropriate action}}
 :::
:::
Topology
拓扑遍历只适用于有向无环图DAG,遍历思路有两种:
(1)一般方法
- 创建queue,将入度为0的顶点enqueue(按顶点序号入队)
- 对已在队列中顶点按顺序dequeue(V),输出V,对V的邻接顶点入度减1,若入度变成0,enqueue
- 不断重复,直到queue为空
当非DAG时,直到queue为空时仍然会有顶点未输出,由此可判断非DAG
(2)逆后根DFS结果
该方法对于非DAG也会产生结果,无法判断是否非DAG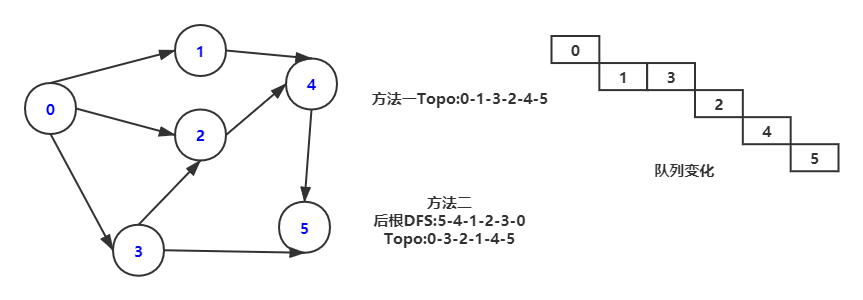
Topo结果不唯一,只要满足优先级限制即可
4. 最短路径问题
给定两点间SP
无法直接在图中得到两个指定点的SP,但可根据”单源SP or 任意顶点对SP”的执行结果得到给定两点间SP
单源SP
| 问题 | 在有向图 G=(V,E) 中,假设每条边权重/距离已知,找到由顶点S到其余各点的最短路径 | 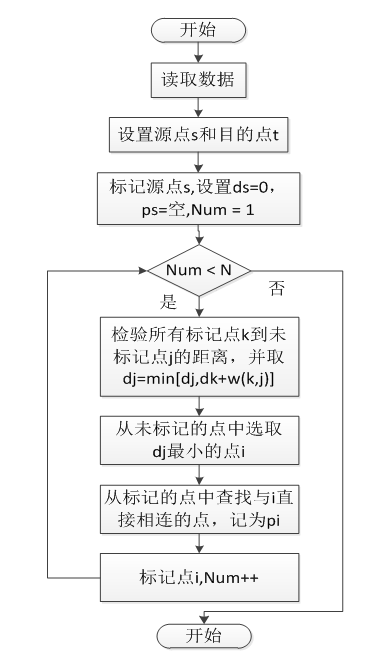 |
|---|---|---|
| 思路 | 1. 求出V到某点长度最短的一条路径 1. 根据1得到的已知最短路径,求出长度次短的路径 1. 依次递推,即可得到顶点V到其余顶点的最短路径 |
每次确定次短路径时遵循
👆上式代表了图算法中最常见的松弛操作: 4.4 最短路径 | |
| 数据结构准备 |
- Dist[]:Dist[k]即起点S->K的SP长度
- Mark[]:Mark[k]=VISTED表示该点已被访问,UNVISTED为未被访问
- Path[]:存放路径倒数第二个顶点,Path[k]即保存S->…->V->K路径的V顶点
| |
| 辅助方法 |
- setMark():标记某个点是否已被访问
- minVertex(G,Dist[]):返回当前SP中,最短路径V->K的起点V
| |
| 实现(起点S)
Dijkstra算法 |
1. **化Dist[]:令起点Dist[S]=0,其余都设为+∞(Integer.MAX VALUE);
1. Dist[]中选取最小值的对应起点V,需保证Mark[V]为UNVISTED:首先将Mark[V]设为VISTED
1. 遍历每个和V直接邻接的顶点W:
比较D[w]【已知S-W最短距离】和D[v] + G.weight(v, w)**【S-V-W距离】,选择更短的路径,更新Dist[w],Path[w]
4. 循环,直到次数等于G.n(),此时对每个顶点都执行了setMark(),即都访问过,通过Path[]可直到起点S到任意点的最短路径,通过Dist[]可知道最短路径的长度
(可以参考右图👉,来自百度百科,觉得蛮清晰) | |
| 时间开销 |
- 下面的算法:
- 外层:Dijkstra()中for循环执行|V|次
- 内层:minVertex()中for循环|V|次,如果更新Dist[],会花费
- 合计
- 对于稀疏图(sparse),使用小顶堆delMin()代替minVertex()可以获得**
| |
// Compute shortest path distances from s, store them in Dstatic void Dijkstra(Graph G, int s, int[] D) {for (int i=0; i<G.n(); i++) // InitializeD[i] = Integer.MAX VALUE;D[s] = 0;for (int i=0; i<G.n(); i++) { // Process the verticesint v = minVertex(G, D); // Find next-closest vertexG.setMark(v, VISITED);if (D[v] == Integer.MAX VALUE) return; // Unreachablefor (int w = G.first(v); w < G.n(); w = G.next(v, w))if (D[w] > (D[v] + G.weight(v, w)))D[w] = D[v] + G.weight(v, w);}}static int minVertex(Graph G, int[] D) {int v = 0; // Initialize v to any unvisited vertex;for (int i=0; i<G.n(); i++)if (G.getMark(i) == UNVISITED) { v = i; break; }for (int i=0; i<G.n(); i++) // Now find smallest valueif ((G.getMark(i) == UNVISITED) && (D[i] < D[v]))v = i;return v;}
:::info
例题:给定有向图,求起点0的单源最短路径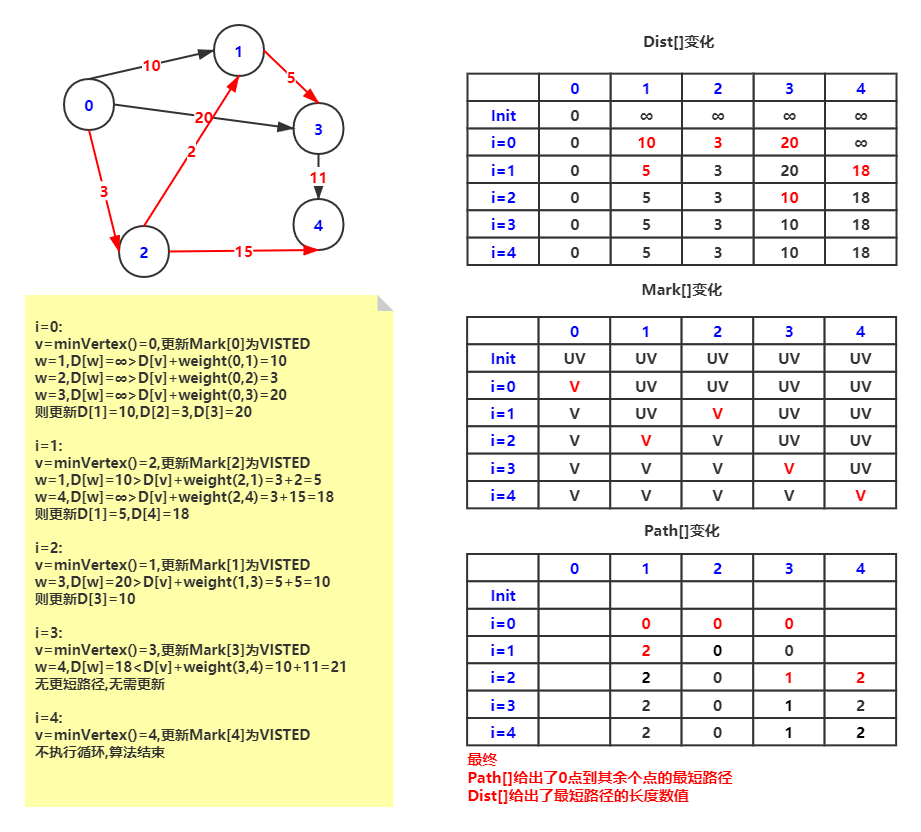 :::
:::
顶点对间SP
| 问题 | 在有向图 G=(V,E) 中,假设每条边权重/距离已知,找到任意顶点对(V,W)的SP |
|---|---|
| 思路 | 方法一:使用|V|次Dijkstra算法,相当于得到每个点的单源SP 方法二:Floyd’s算法,这是一种动态规划算法 给定一个图G,确定(v,w)之间的SP,假设顶点索引为0~(n-1) 初始时图中任意点v直接指向W,我们称之为-1阶路径,意味着中间无过路顶点; 为了找到更短的路径,我们只可能能引入额外的顶点k作为中继 - 对于顶点0,如果d(v,0)+d(0,w)<d(v,w),我们则认为最短0阶路径是V-0-W,否则我们认为最短0阶路径=最短-1阶路径 - … … - 对于顶点k,最短k阶路径只有可能是①v->…->k->w或者②还是最短k-1阶路径 |
因此对于顶点数为n的G来说,想办法推导出任意两点(v,w)的n阶最短路径即可得到任意顶点对(v,w)的最短路径
|
| 数据结构准备 |
- Dist[][]:n阶方阵,Dist[v][w]即保存当前(v,w)的SP,不存在时为∞
- Path[][]:n阶方阵,Path[v][w]=k说明存放(v,w)的SP倒数第二个顶点为k,此时该SP为k阶最短路径,不存在时为-1
|
| 实现(起点S)
Dijkstra算法 |
1.
1.
1.
|
| 时间开销** | |
:::info
举例给定有向图,表示其floyd算法过程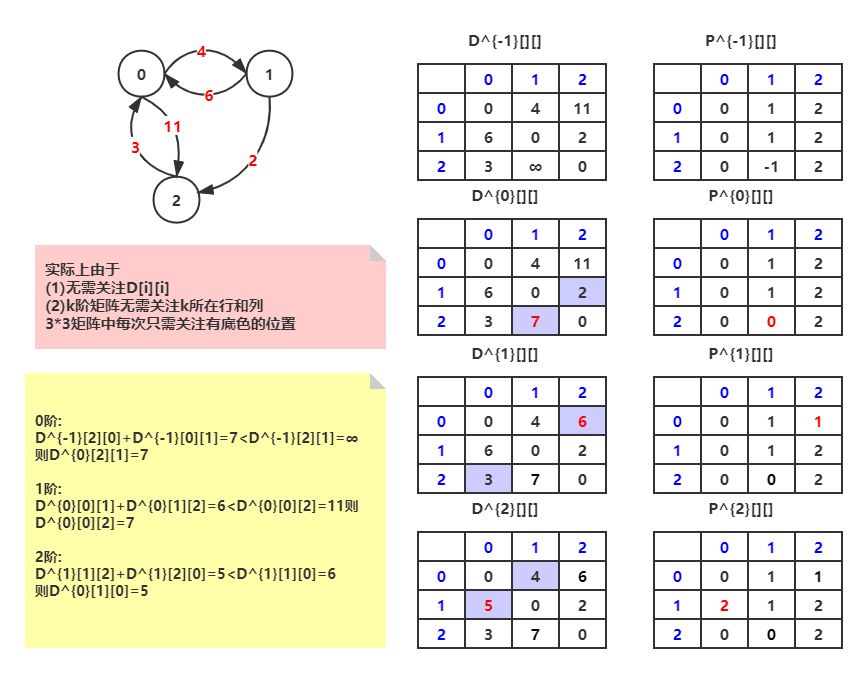 :::
:::
5.最小支撑树问题
| 最小生成树 | - 图的生成树是含有所有顶点的无环连通子图; - 加权图的最小生成树(MST)是一棵权值最小的生成树; |
|---|---|
| 问题描述 | |
| 意义 | 以最小代价连通所有点,可以联系运营商连接不同地区基站 |
Prim算法
| 思路 | 构造树时,|V|个顶点分属两个集合:
- 在树上的点集U
- 不在树上的点集V-U
则每次从连接两集合的边中选出权值最小的加入MST,直到有|V|-1个顶点在MST中 |
| :—-: | —- |
| 开销 |
|
/** Compute a minimal-cost spanning tree */static void Prim(Graph G, int s, int[] D, int[] V) {for (int i=0; i<G.n(); i++) // InitializeD[i] = Integer.MAX VALUE;D[s] = 0;for (int i=0; i<G.n(); i++) { // Process the verticesint v = minVertex(G, D);G.setMark(v, VISITED);if (v != s) AddEdgetoMST(V[v], v);if (D[v] == Integer.MAX VALUE) return; // Unreachablefor (int w = G.first(v); w < G.n(); w = G.next(v, w))if (D[w] > G.weight(v, w)) {D[w] = G.weight(v, w);V[w] = v;}}}
Kruskal算法(避圈法)
| 思路 | 1. 用G的n个顶点构造无边子图Gs 1. 从原图G的最小权边开始添加:若添加它不会使得Gs产生回路则添加,否则选择次小权的边… 1. 重复以上步骤,直到Gs有|V|-1条边 |
|---|---|
| 开销 |
/** Heap element implementation for Kruskal’s algorithm */class KruskalElem implements Comparable<KruskalElem> {private int v, w, weight;public KruskalElem(int inweight, int inv, int inw){ weight = inweight; v = inv; w = inw; }public int v1() { return v; }public int v2() { return w; }public int key() { return weight; }public int compareTo(KruskalElem that) {if (weight < that.key()) return -1;else if (weight == that.key()) return 0;else return 1;}}/** Kruskal’s MST algorithm */static void Kruskal(Graph G) {ParPtrTree A = new ParPtrTree(G.n()); // Equivalence arrayKruskalElem[] E = new KruskalElem[G.e()]; // Minheap arrayint edgecnt = 0; // Count of edgesfor (int i=0; i<G.n(); i++) // Put edges in the arrayfor (int w = G.first(i); w < G.n(); w = G.next(i, w))E[edgecnt++] = new KruskalElem(G.weight(i, w), i, w);MinHeap<KruskalElem> H =new MinHeap<KruskalElem>(E, edgecnt, edgecnt);int numMST = G.n(); // Initially n classesfor (int i=0; numMST>1; i++) { // Combine equiv classesKruskalElem temp = H.removemin(); // Next cheapestint v = temp.v1(); int u = temp.v2();if (A.differ(v, u)) { // If in different classesA.UNION(v, u); // Combine equiv classesAddEdgetoMST(v, u); // Add this edge to MSTnumMST--; // One less MST}}}
:::info
举例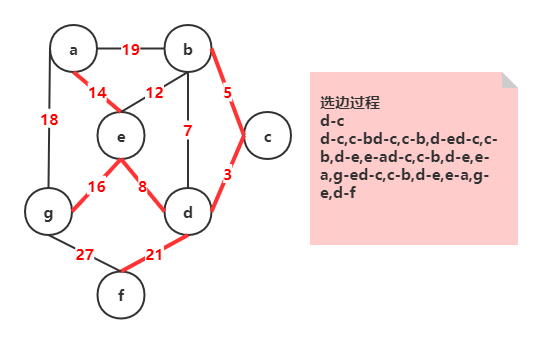 :::
:::
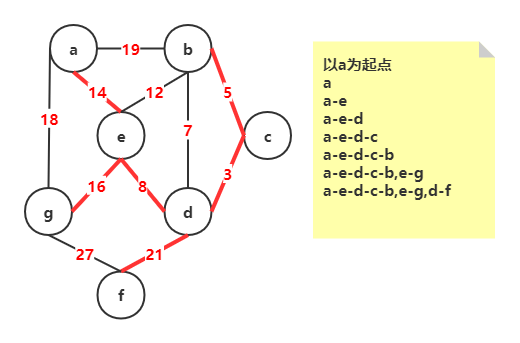 :::
:::

