4.6.1 有向图的强连通性

  • 无向图的连通性:v-w,则v和w互相连通
  • 有向图的可达性:v->w,则从v是单向可达w的
  • 强连通:v<->w,即顶点v和w相互可达,此时v和w是强连通的
    • 有向图的强连通性:当有向图中任意两个顶点互相可达,则有向图是强连通的

4.6.1.1 判断两个顶点是否强连通

  • 当且仅当两个顶点在一个有向环中

4.6.1.2 强连通分量(SCC:Strong Connected Component)

  1. 强连通性是一种等价关系:
    • 自反性:v和自己强连通
    • 对称性:v和w强连通,则w和v强连通
    • 可传递性:v和w强连通,则w和v强连通
  2. 由离散数学知识,等价关系可将点集V分成等价类V,V…,这些子集叫做强连通分量,其定义基于顶点而非边
    • 一个V个顶点的有向图中有1~V个SCC
    • 一个强连通图,只有一个SCC
    • 一个DAG (Directed Acyclic Graph)含有V个SCC

4.6.2 强连通分量API

public class SCC

返回类型 方法 描述
SSC(Digraph G)
boolean stronglyConnected(int v, int w) v和w是否强连通
int count() 图中SCC个数
int id(int v) v所在SCC的标识符

算法4.6 Kosaraju算法

思路

与CC只有几处语句不同

给定有向图G,求出其反向图G 使用DepthFirstOrder计算G逆后序 在原图G中按照G逆后序访问所有未标记结点 在构造函数中,使用id[]和count和CC一样标记同一个连通分量中的结点

实现

  1. public class KosarajuSCC {
  2.     private boolean marked[];//已访问结点
  3.     private int id[];//SCC标识符
  4.     private int count;//SCC个数
  6.     public KosarajuSCC(Digraph G){
  7.         marked = new boolean[G.V()];
  8.         id = new int[G.V()];
  9.         //G反向图的逆后序
  10.         Iterable<Integer> order = new DepthFirstOrder(G.reverse()).reversePost();
  11.         for (int s: order){
  12.             if (!marked[s]){
  13.                 dfs(G,s);
  14.                 count++;
  15.             }
  16.         }
  17.     }
  19.     private void dfs(Digraph G, int v){
  20.         marked[v] = true;
  21.         id[v] = count;
  22.         for (int w:G.adj(v))
  23.             if (!marked[w]) dfs(G,w);
  24.     }
  26.     public boolean stronglyConnected(int w, int v){
  27.         return id[w] == id[v];
  28.     }
  30.     public int id(int v){ return id[v];}
  31.     public int count(){ return count;}
  32. }

算法分析

  • 命题:使用DFS查找G,并根据相反图逆后序访问原图,构造函数中每次递归标记为id[i]的顶点都在一个SSC中

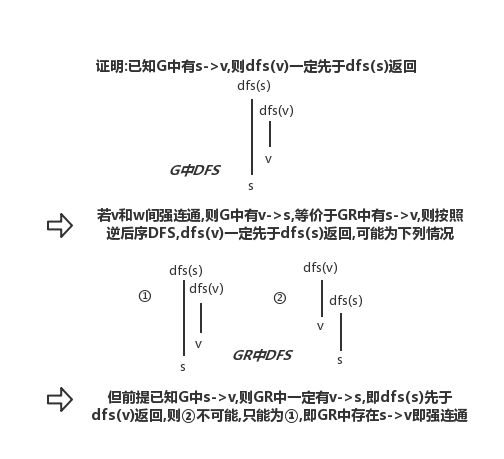
Kosaraju.jpg

  • 命题:Kosaraju算法预处理所需的时间和空间与V+E成正比且支持常数级别的有向图强连通性查询

证明:构造G,reverPost()(DFS一次),访问原图(DFS一次),每一步都和V+E成正比

4.6.3 顶点对可达性与传递闭包

问题:顶点对的可达性:给定图问”是否存在一条从v到w的路径”(非单点/多点可达性或者单点有向路径问题,而是希望建立类似CC类,经过预处理构造后通过connected(v,w)实现常数级别的判断而无需每次重新构造路径)

无向图:即连通性问题,使用基于DFS的CC算法,经过线性级别的预处理时间记录所有连通分量,即可使用connected(v,w)实现常数级别的判断 有向图:不同于强连通分量SCC问题,这时的可达性为单向的,为了实现预处理后常数时间的判断,需要构造传递闭包TransitiveClosure

  • 传递闭包:有向图G的传递闭包由相同顶点构成另一幅图G’,当G’中存在v->w时,当且仅当G中v到w是可达的(G中v到w可达但无直接边,就在G’构造边v->w)
  • 对图构造传递闭包即离散数学中图的可达性矩阵

顶点对可达性API

public class TransitiveClosure

返回类型 方法 描述
TransitiveClosure(Digraph G) 预处理构造
boolean reachable(int v, int w) w是否从v可达

实现

  1. public class TransitiveClosure {
  2.     private DirectedDFS[] all;//传递闭包/可达性为矩阵
  3.     TransitiveClosure(Digraph G){
  4.         all = new DirectedDFS[G.V()];
  5.         for (int v = 0; v < G.V(); v++)//构建矩阵的每一行
  6.             all[v] = new DirectedDFS(G, v);
  7.     }
  9.     boolean reachable(int v, int w){
  10.         return all[v].marked(w);
  11.     }
  12. }