算法5.4 单词查找树

以字符串为键的符号表API

public class StringST

返回类型 方法 描述
StringST() 创建符号表
void put(String key, Value val) 插入键值对
Value get(String key) key对应值
void delete(String key) 删除key以及值
boolean contains(String key) 是否含有key的值
boolean isEmpty() 符号表是否为空
String longestPrefixOf(String s) s前缀中最长的键
Iterable keysWithPrefix(String s) 所有以s为前缀的键
Iterable keysThatMatch(String s) 所有和s匹配的键
int size() 键值对数量
Iterable keys() 所有和s匹配的键

算法5.4 (R向)单词查找树

  1. 基本性质
    • 将每个键(String)关联值(Value)保存在该键最后一个字母对应结点中
    • 值为null的键在符号表中无对应键,存在为了简化单词查找树中的查找
  1. public class TrieST<Value>{
  2.     private static int R = 256;
  3.     private Node root;
  4.     ...
  5. }
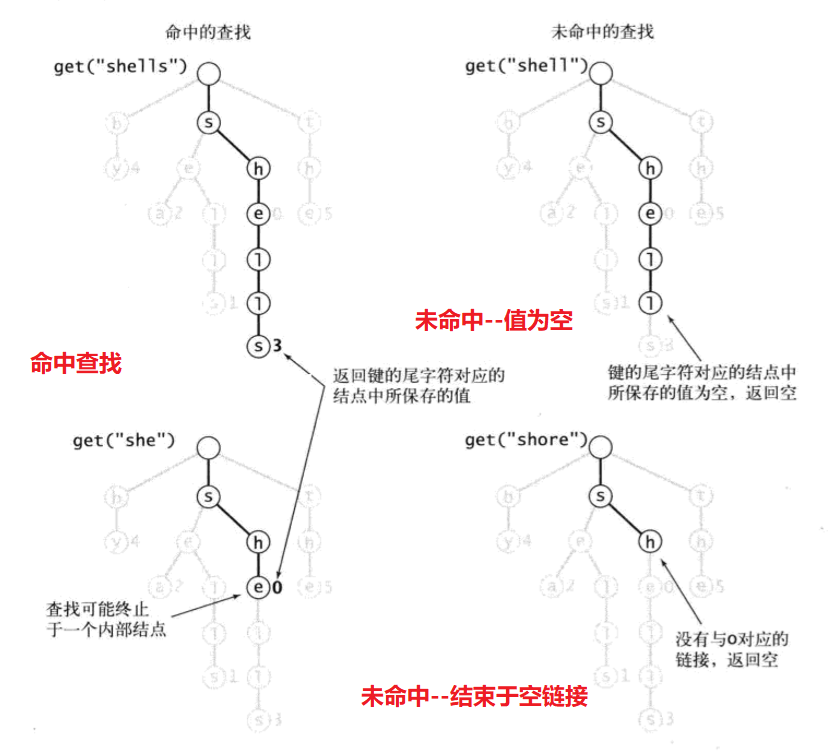
  1. 查找:从首字母链接开始,到下一个结点对应第二个字母的链接…不断向下,直到键最后一个字母对应结点或遇到空链接
    • 键尾字符对应结点值非空—查找命中
    • 键尾字符对应结点值为空—未命中,符号表中不存在被查找的键
    • 查找结束于空链接—未命中
  1. public void get(String key){
  2.     Node x = get(root, key, 0);
  3.     if(x == null) return null;//未找到,返回null
  4.     return (Value)x.val;
  5. }
  6. private Node get(Node x, String key, int d){
  7.     if(x == null) return null;//空链接
  8.     if(d == key.length()){ return x;}
  9.     char c = key.charAt(d);//找到第d个字符对应子单词查找树
  10.     return get(x.next[c], key, d+1);
  11. }
  1. 插入:和BST一致,插入就是先进行查找,直到树中尾字符的结点或空链接
    • 先遇到空链接:此时树中无插入结点,则需要为每个字符创建一个新结点将值保存在末尾
    • 先遇到尾字符:此时树中已有插入结点,则更新值
  1. public void put(String key, Value val){
  2.     root = put(root, key, val, 0);
  3. }
  4. private Node put(Node x, String key, Value val, int d){
  5.     if(x == null) x = Node();//空链接,创建新结点
  6.     if(d == key.length()){ x.val = val; return x;}
  7.     char c = key.charAt(d);//找到第d个字符对应子单词查找树
  8.     x.next[c] = put(x.next[c], key, val, d+1);
  9.     return x;
  10. }
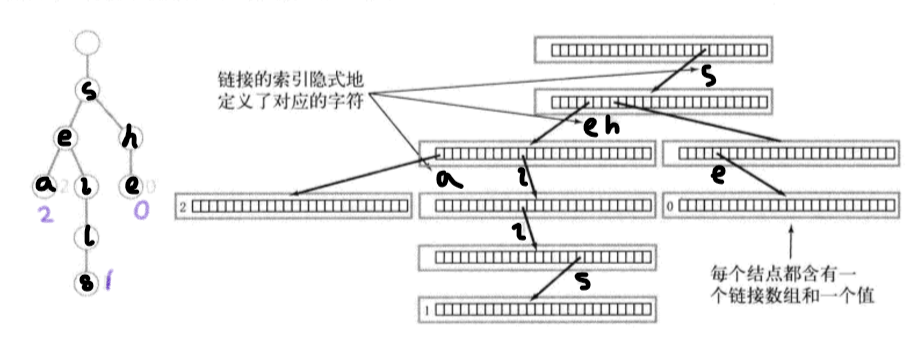
  1. 结点的表示
    • 每个结点含有R个链接,对应每个可能字符
    • 字符和键值隐式的保存:如sea,数据结构中没有”s””e””a”,但通过从根结点到最后结点每段路径的链接位置19->5->1标识
  1. //内部类
  2. private static class Node{
  3.     private Object val;//无法定义泛型数组
  4.     private Node[] next = new Node[R];
  5. }

node.png

  1. 大小:统计树中键的数量
    • 即时实现:设置实例变量N,在put()和delete()时更新
    • 延时实现:递归遍历所有结点
  1. //递归延时实现:牺牲性能
  2. public int size(){ return size(root); }
  3. private int size(Node x){
  4.     if(x == null) return 0;
  5.     int cnt = 0;
  6.     if(x.val != null) cnt++;
  7.     for(char c = 0; c < R; c++)
  8.         cnt += size(next[c]);
  10.     return cnt;
  11. }
  1. 查找所有键
    • BST中Node有val变量,所以可以通过遍历BST后将val放入队列完成所有查找
    • SST中没有显式保存字母,需要实现collect():将字符显示入队同时进入下个字符链接,查找所有键时,使用””为前缀,调用keysWithPrefix(),方法中先使用get()获得给定前缀的查找树
  1. public Iterabel<String> keys(){
  2.     return keysWithPrefix("");
  3. }
  4. public Iterable<String> keysWithPrefix(String pre){
  5.     Queue<String> q =  new Queue<>();
  6.     collect(get(root, pre, 0));
  7.     return q;
  8. }
  9. private void collect(Node x, String pre, Queue<String> q){
  10.     if(x == null) return;
  11.     if(x.val != null) q.enqueue(pre);
  12.     //当x!=null且x.val==null时,即一个中间字符,继续调用collect()
  13.     for(char c = 0; c < R; c++)
  14.         collect(x.next[c], pre + c, q);
  15. }

STget.png

  1. 通配符匹配
    • 以”.”为通配符,一个.代表一个字母,执行keysThatMatch(“.he”),结果会是she,the等,keysThatMatch(“s..”),结果会是sea,she
    • 修改collect(),入队条件扩充为(d == pat.length() && x.val != null),没有前半句会匹配出字符数不达标的String
  1. public Iterable<String> keysThatMatch(String pat){
  2.     Queue<String> q = new Queue<String>();
  3.     collect(root, "", pat, q);
  4.     return q;
  5. }
  6. private void collect(Node x, String pre, String pat, Queue<String> q){
  7.     int d = pre.length();
  8.     if(x == null) return;
  9.     if(d == pat.length() && x.val != null) q.enqueue(pre);
  10.     if(d == pat.length()) return;
  12.     char next = pat.charAt(d);
  13.     //当x!=null且x.val==null时,即一个中间字符,继续调用collect()
  14.     for(char c = 0; c < R; c++)
  15.         if(next == '.' || next == c)
  16.             collect(x.next[c], pre + c, pat,  q);
  17. }
  1. 最长前缀
    • 给定字符串,返回其前缀中最长的键:如longestPrefixOf(“shell”),返回she,longestPrefixOf(“shells”)返回shell
  1. public String longestPrefixOf(String s){
  2.     int length = search(root, s, 0, 0);
  3.     return s.substring(0, length);
  4. }
  5. private int search(Node x, String s, int d, int length){
  6.     if(x == null) return null;//空链,停止
  7.     if(d == s.length()) return length;//字符串本身为键
  8.     if(x.val != null) length = d;
  9.     char c = s.charAt(d);
  10.     return search(x.next[c], s, d+1, length);
  11. }
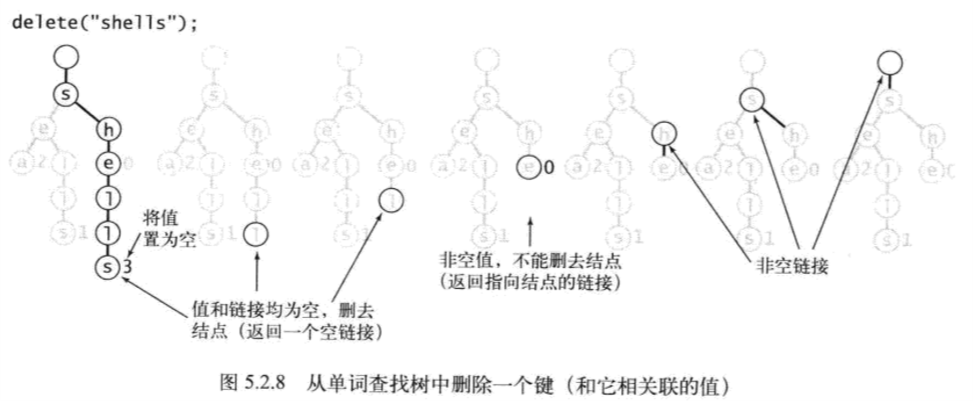
  1. 删除
    • 在SST中删除,找到键对应结点,将值设为null,若结点后还指向某个子结点,则无需其他操作
    • 若结点后所有链接都为空,则需要删除结点,若删去它后父结点为空,则继续删去父结点
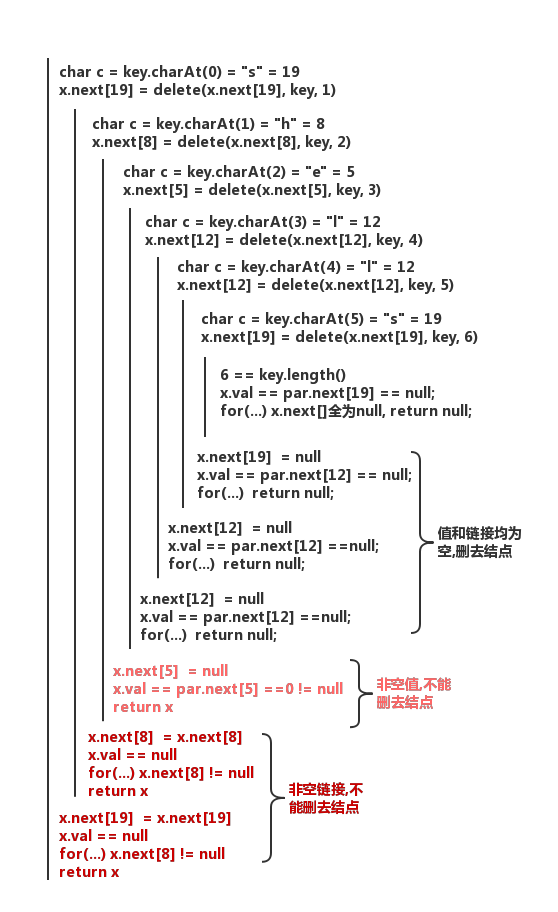
  1. public void delete(String key){
  2.     root = delete(root, key, 0);
  3. }
  4. private Node delete(Node x, String key, int d){
  5.     if(x == null) return null;
  6.     if(d == key.length()) x.val = null;//找到结点,值设为null
  7.     else{
  8.         char c = key.charAt(d);
  9.         x.next[c] = delete(x.next[c], key, d+1);
  10.     }
  11.     if(x.val != null) return x;
  12.     for(char c = 0; c < R; c++)
  13.         if(x.next[c] != null) return x;
  14.     return null;
  15. }

delete2.png
delete.png

算法分析

  • 单词查找树的链表结构和键的插入或删除顺序无关:给定的一组键,树是唯一的
  • 单词查找树中查找或插入一个键,访问数组次数最多为键长度加1

证明:put()和get()递归中的参数d,初始0,进入最后一次递归时x.next[c] = put(x.next[c], key, val, d+1),此时d=key.length()

  • 字母表大小R,对N个随机键构造的查找树中,未命中查找平均需要检查~logN个结点,未命中查找成本与键的长度无关

证明:见书P484

  • 一棵单词查找树中链接总数在RN到RNw间,w为键平均长度
    • 缩小R可节省大量空间

证明:树中,每个键有一个结点保存值,同时一个结点关联R个链接,因此假设最好情况N个键有N个结点,则RN个链接,但若所有键首字母都不同,每个键的每个字母都有一个对应结点,链接为R乘所有键中字符总数:RNw