算法描述

  • 描述1:初始化distTo[s]为0,其余distTo[]为∞,之后逐个将distTo[]中最小非树结点放松,直到所有结点都在树中或所有非树结点distTo[]为∞(s不可达)
  • 描述2:初始化后从s开始放松:将与s间隔一条边的顶点加入队列中,按权值小到大对所有间隔一条边结点都进行放松,然后是间隔两条边…结束条件同上

数据结构

  • distTo[]:标记s->w的最短距离
  • edgeTo[]:标记s->w最短路径的最后一条边
  • IndexMinPQ:以”w”为索引,distTo[w]为键的索引优先队列,delMin()保证可以删除并返回路径最短的顶点

算法证明

证明:若v是起点可达的,v被放松时一定满足distTo[w]<=distTo[v]+e.weight(),放松v前的结点时,delMin()保证了distTo[v]一定是最小的,不会再改变,则distTo[w]只会变小,如此对每个顶点distTo[]都是最小的,且满足distTo[w]<=distTo[v]+e.weight(),根据最短路径最优性条件(书P420),则得到的distTo[]都是最短路径长度

实现

  1. import edu.princeton.cs.algs4.IndexMinPQ;
  2. import edu.princeton.cs.algs4.Stack;
  4. public class DijkstraSP {
  5.     private DirectedEdge[] edgeTo;
  6.     private double[] distTo;
  7.     private IndexMinPQ<Double> pq;
  9.     public DijkstraSP(EdgeWeightedDigraph G, int s){
  10.         edgeTo = new DirectedEdge[G.V()];
  11.         distTo = new double[G.V()];
  12.         pq = new IndexMinPQ<>(G.V());
  14.         for (int v = 0; v < G.V(); v++)
  15.             distTo[v] = Double.POSITIVE_INFINITY;
  17.         distTo[s] = 0.0;
  18.         pq.insert(s, 0.0);
  19.         while (!pq.isEmpty()){
  20.             relax(G, pq.delMin());
  21.         }
  23.     }
  25.     private void relax(EdgeWeightedDigraph G, int v){
  26.         for (DirectedEdge e: G.adj(v)){
  27.             int w = e.to();
  28.             if (distTo[w] > distTo[v]+e.weight()){
  29.                 distTo[w] = distTo[v]+e.weight();
  30.                 edgeTo[w] = e;
  31.                 if (pq.contains(w)) pq.change(w, distTo[w]);
  32.                 else pq.insert(w, distTo[w]);
  33.             }
  34.         }
  35.     }
  37.     public double distTo(int v){ return distTo[v];}//s->v的距离
  38.     public boolean hasPathTo(int v){ return distTo[v] < Double.POSITIVE_INFINITY;}
  39.     public Iterable<DirectedEdge> pathTo(int v){
  40.         Stack<DirectedEdge> stack = new Stack<>();
  41.         for(DirectedEdge e = edgeTo[v]; e != null; e = edgeTo[e.from()])
  42.             stack.push(e);
  43.         return stack;//后根入栈
  44.     }
  45. }

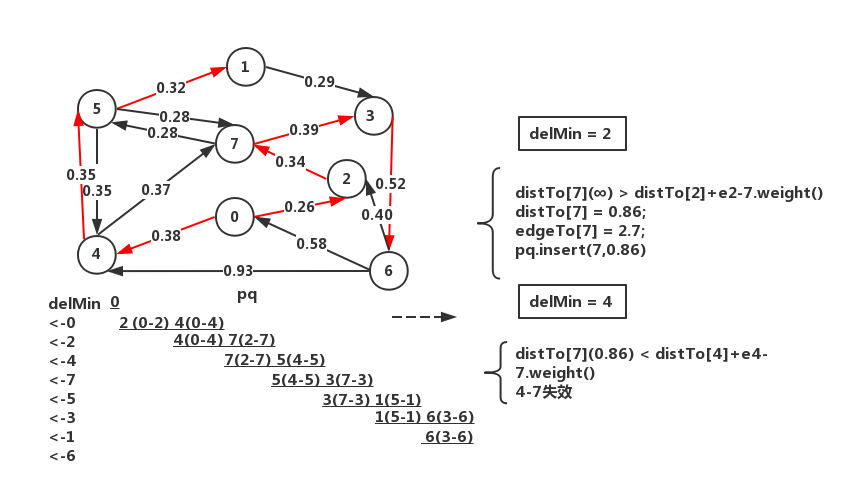
示例

Dijkstra.jpg

算法分析

  • G(V,E)中使用Dijkstra算法构建SPT所需空间和V成正比,时间和ElogE成正比(最坏)

证明:与使用索引优先队列的Prim一致

任意两顶点间最短路径

  • 与算法4.6中建立传递闭包获得顶点对可达性类似,通过建立DijkstraSP[]判读顶点s,t直接知否有最短路径,已经最短路径大小
  1. public class DijkstraAllPairsSP {
  2.     private DijkstraSP[] all;
  3.     public DijkstraAllPairsSP(EdgeWeightedDigraph G){
  4.         all = new DijkstraSP[G.V()];
  5.         for (int v = 0; v < G.V(); v++){
  6.             all[v] = new DijkstraSP(G, v);
  7.         }
  8.     }
  9.     //返回s->t最短路径
  10.     Iterable<DirectedEdge> path(int s, int t){ return all[s].pathTo(t);}
  11.     //返回s->t最短路径大小
  12.     double dist(int s, int t){ return all[s].distTo(t); }
  13. }