1. 概述

树状图是一种数据结构，它是由n(n≥0)个有限结点组成一个具有层次关系的集合.把它叫做”树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的.它具有以下的特点：

  • 每个结点有零个或多个子结点;
  • 没有父结点的结点称为根结点;
  • 每一个非根结点有且只有一个父结点;
  • 除了根结点外，每个子结点可以分为多个不相交的子树;

2. 遍历

由于一般树的子结点可有不止2个，此时无法定义中序遍历，以此对于非二叉树只有两种遍历：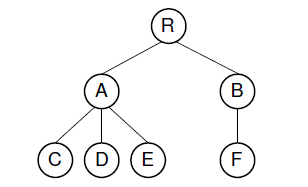
image.png
Ch6 (非二叉)树 - 图2

3. 树的并查算法(UNION/FIND)

描述

  • UNION：对于多个不相交集合(disjoint sets)，希望支持两个基本操作(1)判断两个对象是否在一个集合中，然后(2)合并两个对象所在集合
  • FIND：如果给定两个结点，问它们是否属于同一颗树，可行的方法是上溯两个结点的最终根结点，如果根结点相同，一定属于同一棵树，FIND旨在找出最终根结点

    应用

    可能直接看到并查算法的描述一脸懵逼👶，看下应用： :::info “等价类”问题是并查算法的用途之一，这涉及离散数学中的等价关系(满足自反/对称/传递性)

Ch6 (非二叉)树 - 图3 :::

实现

ParPtrTree.java
本书上使用“父指针树ParPtrTree”实现并查算法(也可以对比《算法》中的并查算法)

  1. 初始时针对n个对象创建大小n的数组array，每个对象和每个元素下标建立唯一的对应关系，其中每个元素值暂时初始化为null，这个数组即存储当前对象的最终根结点
  2. 输入等价关系(a，b)
    1. 执行differ(a，b)，通过find(a)，find(b)在array[a]和array[b]找到二者的最终根结点root1和root2，若不等，则不属于一个树，进入下一步
    2. 执行union(a，b)，同样root1和root2，使得array[root2]=root1，即使得两个原本独立的树拥有共同的根节点，二者被合并 :::info Ch6 (非二叉)树 - 图4
      首先初始化，创建array[6]
      ParPrtTree-1.png
      (A，B)：root1=find(0)=0，root2=find(1)=1，array[root2]=root1=0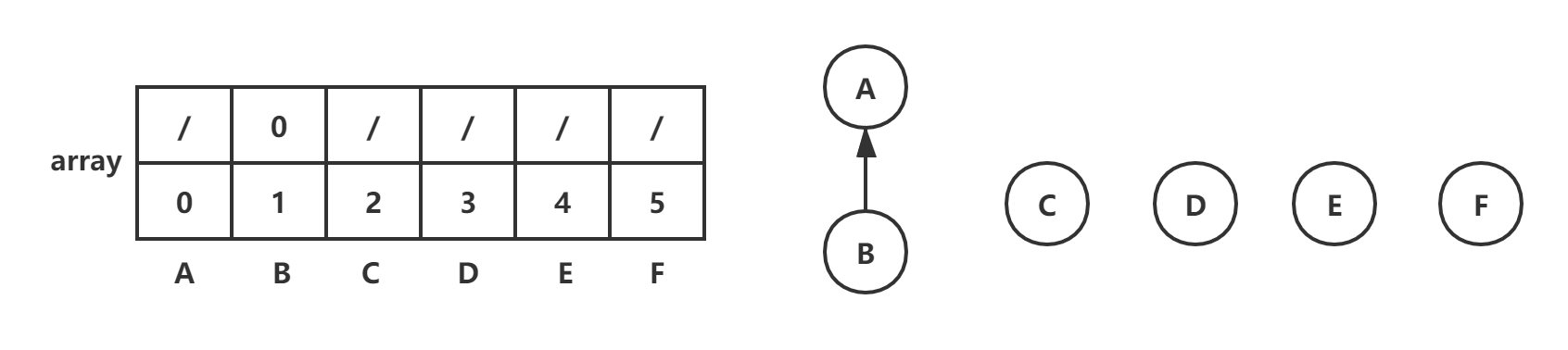
      ParPrtTree-2.png
      (A，C)：root1=find(0)=0，root2=find(2)=2，array[root2]=root1=0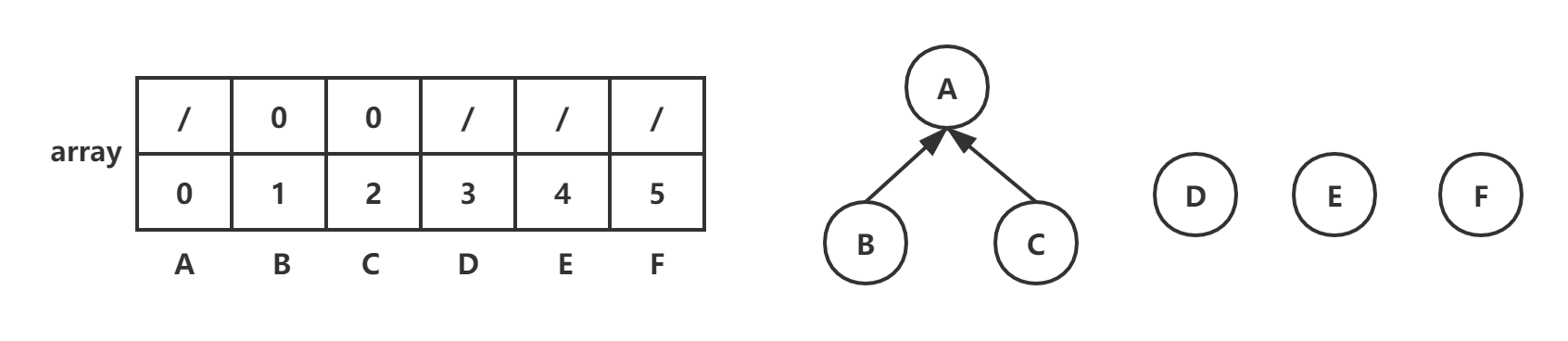
      ParPrtTree-3.png
      (C，E)：root1=find(2)=0，root2=find(4)=4，array[root2]=root1=0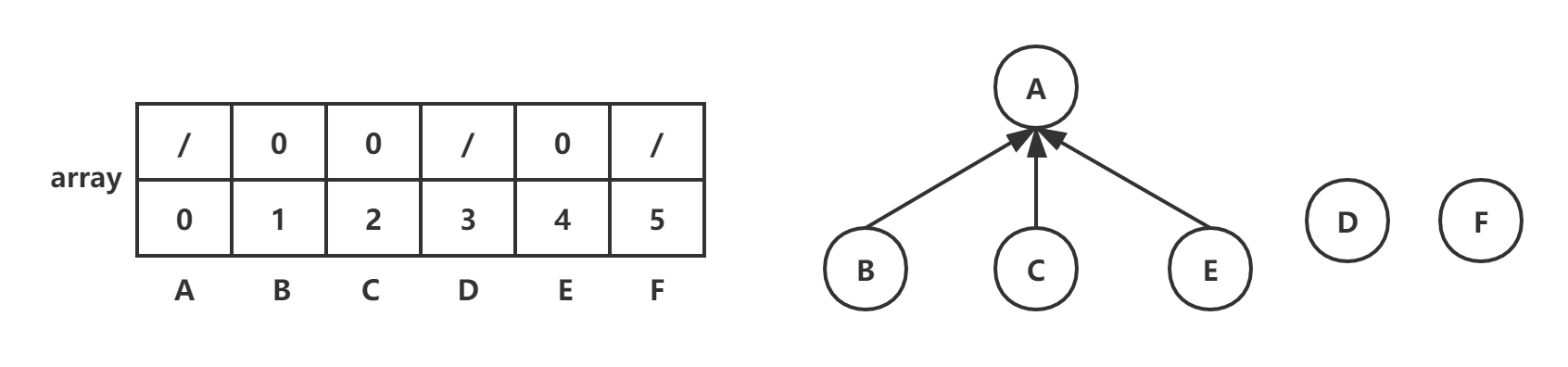
      ParPrtTree-4.png
      (F，D)：root1=find(5)=5，root2=find(3)=3，array[root2]=root1=5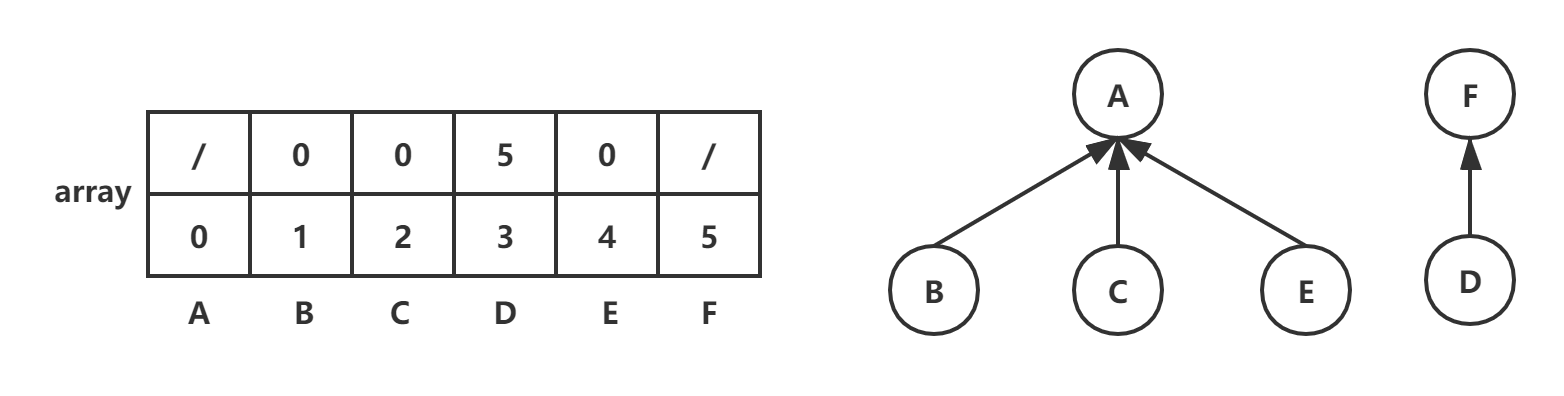
      ParPrtTree-5.png
      (F，A)：root1=find(5)=5，root2=find(0)=0，array[root2]=root1=5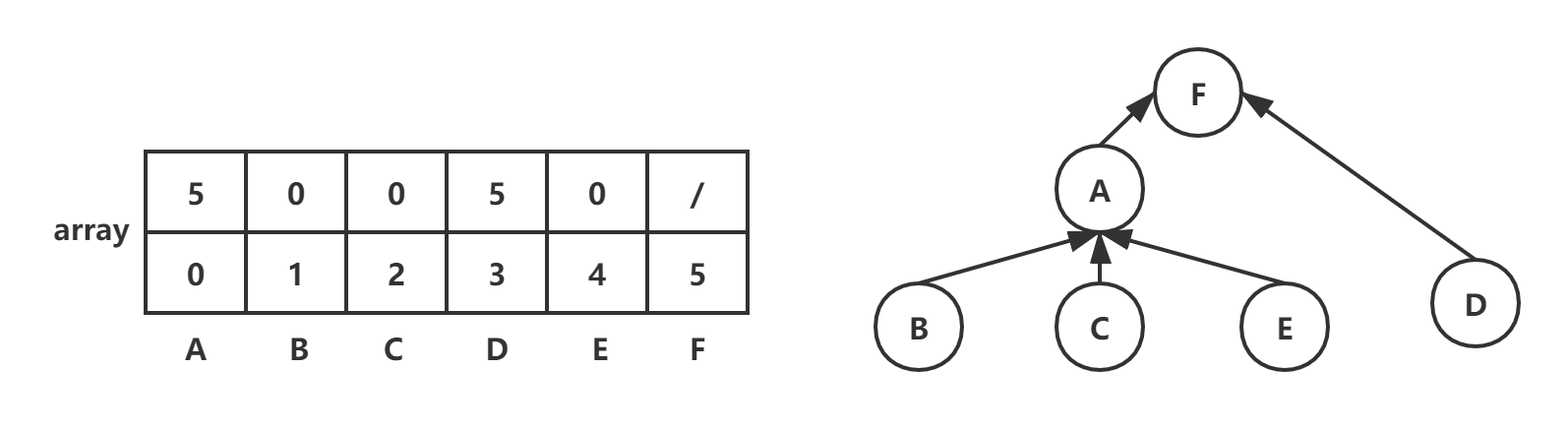
      ParPrtTree-6.png :::

      UNION()优化：加权合并

      默认的”父指针树ParPtrTree”在union()时因为(a，b)顺序的固定会导致一棵结点个数多的树连接到一棵结点数少的树上，即”大树挂小树”，导致生成的树不平衡，我们应使得”小树挂大树”
      具体的实现应该是额外维护一个数组用于存储各个根结点的结点数(权重)，在union()时先比较权重确定小树和大树
      实现可参考1.5.3 加权quick-union算法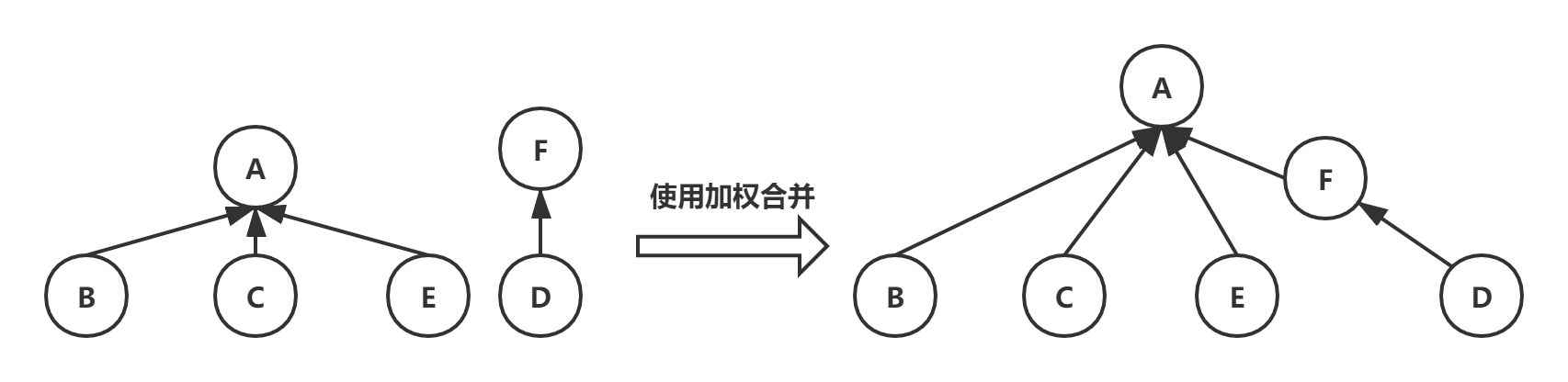
      加权合并.png

      FIND()优化：路径压缩

      在查找结点的根结点时，将当前结点直接连接到根结点上
      实现可参考1.5.4 路径压缩的加权quick-union算法(最优算法)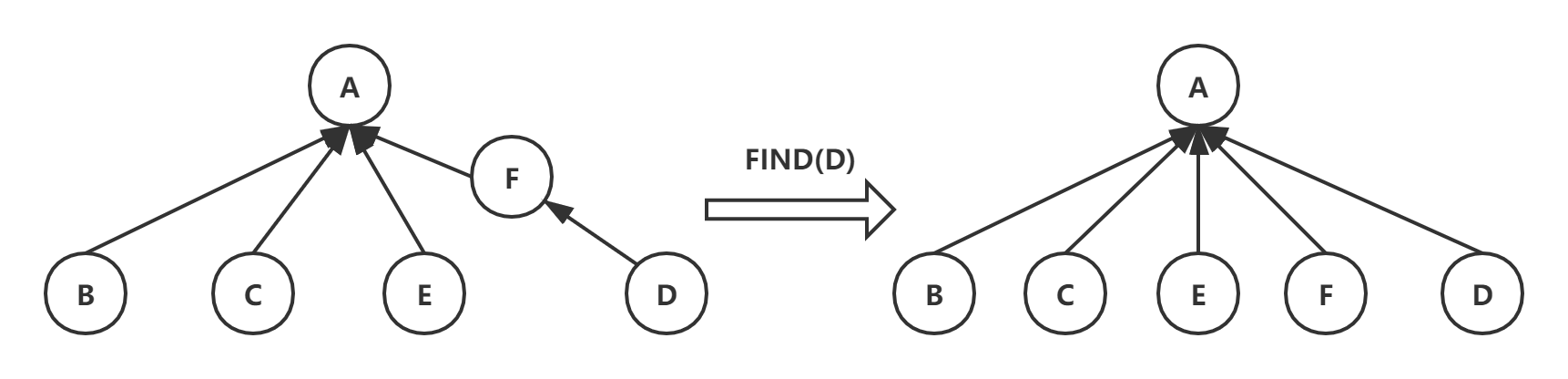
      路径压缩.png

4. 树与二叉树变换

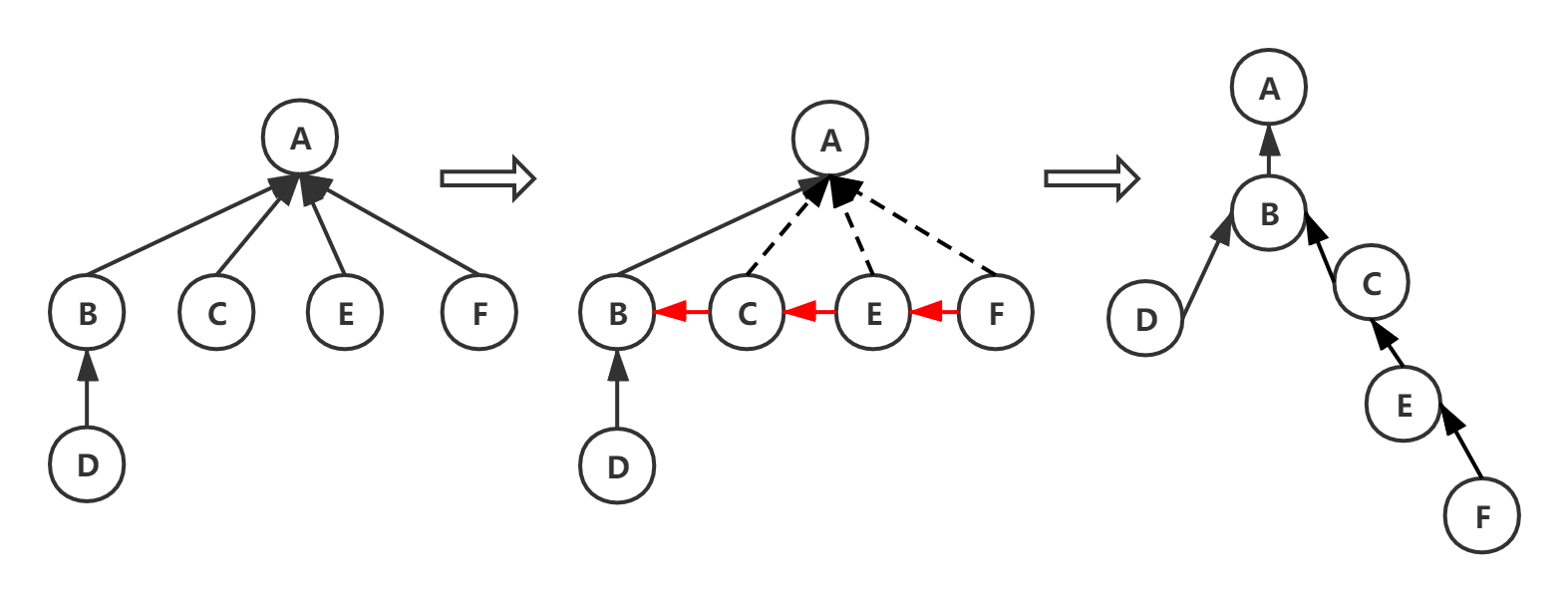
树->二叉树

  1. 同父结点的兄弟结点相连
  2. 对树中非父亲结点的第一个孩子结点，只保留其第一步新加的连线
  3. 整理为二叉树形式

T-BT.png

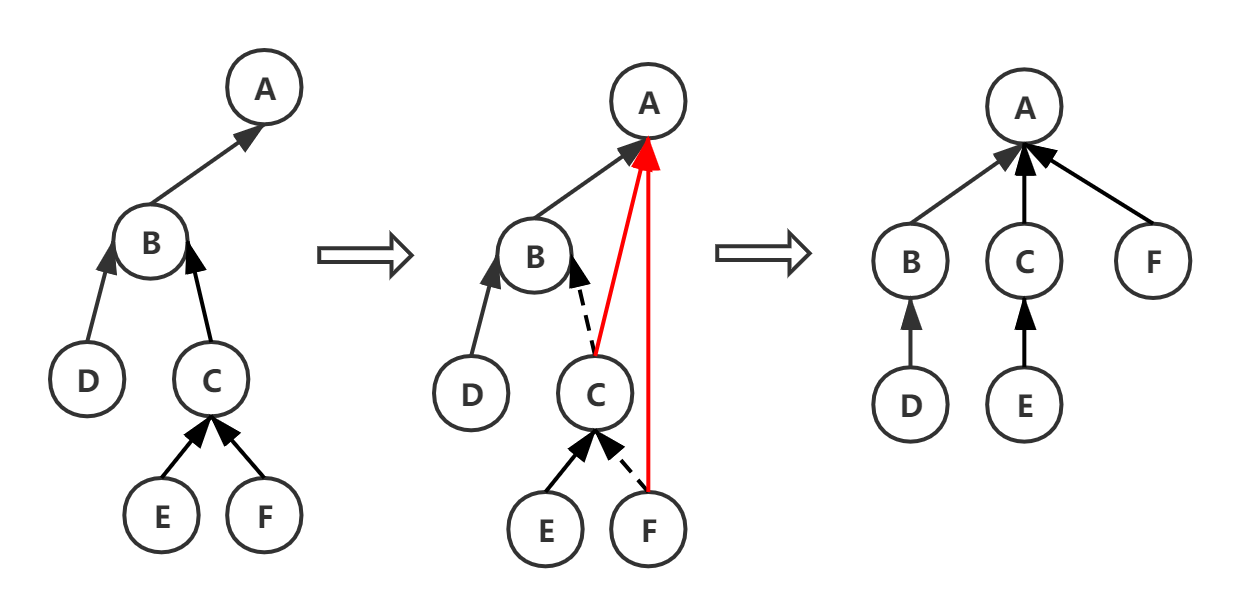
二叉树->树

  1. 某个结点(A)是其父结点(B)的左孩子时，把该结点的RC，RC.RC，…都与其父结点(A)连接
  2. 删除原始二叉树中那些RC，RC.RC，…与各自父结点的连线
  3. 整理为树的形式

BT-T.png