SQL
1. 基本查询结构

⭐尽管典型的查询语句为SFW顺序,但真正的理解顺序为:
- from:对m个关系求笛卡尔积,产生候选元组集合
- where:依据谓词P对候选元组选择,只有使P为true时,将元组t加入结果关系(当省略P时,P默认为true)
- select:对结果关系进行指定属性的投影
2. 附加的基本运算
更多见: mid-term _Review
| 字符串操作 | 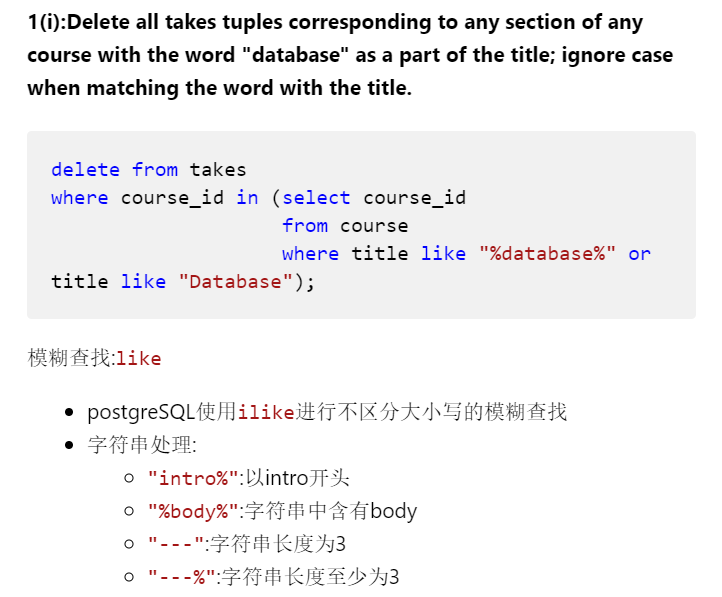 |
|---|---|
| 结果排序 |  |
3. 聚集函数⭐
| 基本 | SQL提供五个基本聚集函数:
- avg
- max
- min
- sum
- count
聚集函数不能直接出现在where语句中(可以在嵌套查询中使用):where salary > max(salary)❌ | 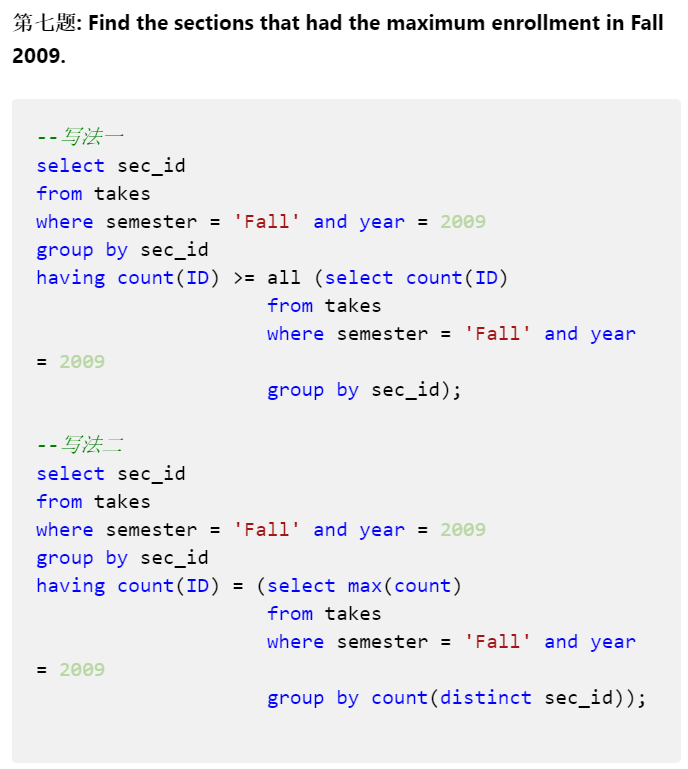 |
| :—-: | —- | :—-: |
| group by | group by语句通常使用在聚集函数后,对查询结果进行分组
|
| :—-: | —- | :—-: |
| group by | group by语句通常使用在聚集函数后,对查询结果进行分组
- 出现在select子句后的非聚集函数属性必须也在group by后出现,但group by后的属性不必都在select后出现
| |
| having | having通常在group by后使用,非单独子句,用于筛选分组结果 | |
4. 嵌套子查询
4.1 嵌套查询
| in/
not in | 先进行内查询,将结果视为集合常量与外表连接,再进行外查询
- 适合外表大,内表小
- 不适合内表记录有NULL的情况,当内表有NULL,内查询不返回记录
参考链接: 浅谈sql中的in与not
in,exists与not exists的区别以及性能分析
|
| :—-: | —- |
| exists/
not
exists | 对外表元组集合做for循环,依次带入内表查询,查询结果非空时返回true |
| 相关子查询
(correlated) | 当外层的查询名称可以用在where子句的查询中,称为相关子查询 |
|  | |
| |
4.2 集合比较
| some | 至少有一个满足就成立 - =some等价于in - <>some不等价于not in,不存在逻辑关系 |
|---|---|
| all |
所有都要满足 - =all不等价于in - ✔当子句是标量子查询(scalar subquery),当一般等号使用 - ❌当子句返回集合,=all()的结果集为NULL - <>等价于not in |
| 最值问题 | - 使用>=all()或<=all()进行内外查询比较 - 内查询使用max()/min()找出最值,外查询使用=比对 |
| with子句 |
with提供了定义临时关系的方法,当嵌套查询过于复杂时,可提前使用with在查询开始定义关系 |
4.3 集合包含问题⭐
(空关系测试)
使用not exitst语句测试子查询结果集中是否不存在元组:
5. 数据库修改
5.1 删除
标准语句:
delete from where
关于delete执行顺序:
delete from instructorwhere salary < (select avg(salary) from instructor);
执行中,avg(salary)在delete元组前就已经计算得到,不会因为删除和查询同时对于instructor而冲突
5.2 插入
标准语句: ```sql // 形式一:自行输入插入数据 insert into table T values (r1, r2, r3);
// 形式二:从已有数据中选取插入数据 insert into table T select r1, r2, r3 from B;
<a name="OmCBT"></a>#### 5.3 更新- **标准语句**```sqlupdate T set r1 = r1';

6. 连接表达式
6.1 连接
| 连接类型 | 连接条件 |
|---|---|
- 内连接inner join: 最常用,默认的常规连接 - 左外连接left outer join: 对左侧失配字段,右侧用null填充 - 右外连接right outer join: 对右侧失配字段, 左侧用null填充 - 全外联结full outer join: 对两侧失配字段都保留 |
- 自然连接 natural join:默认对共有字段连接,重复字段只显示一次,失配字段丢失 - 条件连接 on:条件复杂时,using可接限制子句 - 条件连接 using:条件简单时,可能是指定某同名属性 |
| 例题 | |
给定关系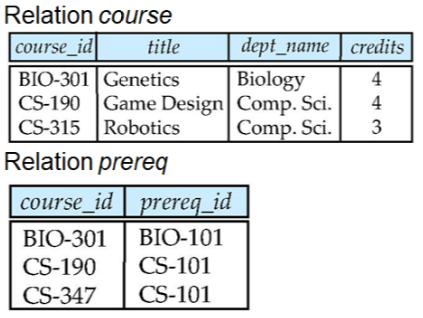 |
自然(内)连接:course natural |
join prereq中左侧CS-315发生失配,要想不丢掉数据,需要使用:course left outer join prereq oncourse.course_id
= prereq.course_id |
|
- 左/右/全外连接与内连接图示
参考链接: 【概念区分】笛卡尔积,自然连接,内连接,外连接(左,右,全)
6.2 连续连接
在SQL中,from语句允许一般化为以下格式
select A1, A2 … Anfrom E1, E2, … ,Enwhere P;
其中Ei可以是单独关系模式R,也可以是自然连接语句,R1 natural join R2, 因此SQL中from中可以有三种搭配:
- 纯笛卡尔积: from R1, R2, R3
- 纯自然连接: from R1 natural join R2 natural join R3
- 混合: from R1 natural join R2, R3(不推荐)
但是对于给定关系模式,不同的连接结果可能不同,给定
- course(course_id, title, dept_name, credits)
- instructor(ID, name, dept_name ,salary)
- teaches(ID, course_id, sec_id, semester, year)
有以下两种选择:
// 1select name, titlefrom instructor natural join teaches, coursewhere teaches.course_id = course.course_id;// 2select name, titlefrom instructor natural join teachesnatural join course;
结果不同,intructor与teaches自然连接后—(ID, name, dept_name, salary, course_id, sec_id, semester, year)
- 如果与course自然连接,需要满足属性集(course_id, dept_name)的完全匹配(不能只有一个属性相等)
- 如果使用where限定的笛卡尔积只用满足course_id上的相等即可被选出
因此,推荐使用using或者on语句,避免了自然连接与笛卡尔积混用,又保证了选择的有效性:
select name, titlefrom instructor natural join teaches join course using(course_id);
关系代数
1. 基本运算
参考链接: Ch2 关系查询语言
| 选择运算 | 对应语句where,用于选择元组,谓词可使用and(∩),or(∪),not(∽)合并 符号:小写sigma:σ |
|---|---|
| 投影运算 | 对应语句select,用于列选择 符号:大写pi: Π |
| 集合并 | 对应操作select r from T and select s from |
T
符号:Π1+Π2
为了使r∪s有意义:
- r和s同元,即属性数目相同
- r和s的属性域对应相同
|
| 集合差 | 对应操作select r from T except select s
from T
符号:Π1-Π2
r-s意义:包含在r但不包含在s中的关系,有意义的条件和集合并相同 |
| ⭐笛卡尔积 | 对应语句select r from T, S
符号:Π(σ(T×S))
区分笛卡尔积和连接,如果使用join代替”,”就成了连接,非笛卡尔积 |
| 更名 | 对应语句E as x,将x赋给表达式E做别名
符号:小写rho:ρx(E) |
2. 附加运算
| 集合交 | 对应查询:找出既在2009秋开设也在2010年春开设的课程
符号:Π1∩Π2
关系代数表达式中没法直接实现交运算,而是使用r∩s=r-(r-s),∩只是方便表达, |
| :—-: | —- |
| 自然连接 | 对应语句:natural join
符号:σ(r⋈s)
当r与s没有任何相同属性时,r⋈s=r×s |
| | theta**连接⭐
对应语句:join on
自然连接的扩展,可以将选择运算和笛卡尔积合并,考虑关系r(R)和s(S),设θ是R∪S属性上谓词,则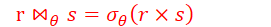
 |
| 聚集函数
|
| 聚集函数
&
分组 |
- 对于聚集函数,使用 等表示
等表示
- 当考虑到避免重复时,使用count-distinct()
- select后除聚集函数外的属性都要出现在group后,因此遇到分组时,省略Π投影,直接将属性写在前面(参考上图)
|
| | 个人理解
Π投影选择需要的属性(列),当不进行Π投影,表示属性全选,即整个元组,不要过分纠结于Π投影和G的内外,具体情况具体分析,比如某地当需要count(course_id)>5时的student_id,此时Π就需要在G外侧再次选择一次student_id,否则结果元组会带着count属性 |
| 除法运算 | 对应查询:集合包含问题
符号:σ(r⋈s)**
参考链接: 关系代数中的除法运算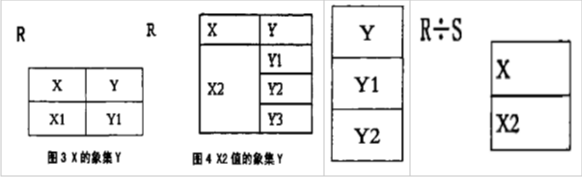
R÷S,即R中X的每个x对应的像集Y包含S中Y属性的所有值 |
|