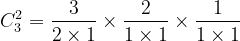要求:估计用以下代码计算binomial(100, 50, 0.25)的次数
private static double binomial(int N, int k, double p){ if(N == 0 && k == 0) return 1.0; if(N < 0 || k < 0) return 0.0; return (1.0 - p)*binomial(N-1, k, p) + p*binomial(N-1, k-1, p);}
解析:
约分即得到组合数递推公式
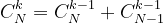
问题:
该方法一个递归就产生两个子递归,运算量非常大,如题数据会一直计算无法得到结果
改进方法:
思路:
已知二项概率公式和组合数公式
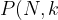 =C_N^kp^k(1-p)^{N-k}#)
=C_N^kp^k(1-p)^{N-k}#)
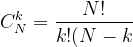 !}#)
!}#)
先计算组合数,但当N较大很大时,阶乘会超出int类型值域,所以需要每次乘一项后就约分为最简形式,可以使用求最大公约数的算法
例:
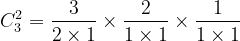
pubilc class Ex1_1_27{ //计算组合数 private static double Combine(int X, int Y, int Z){ if(x == 0 && Y == 0 && Z == -1){ return 1; } if(x == 0) x = 1; if(Y == 0) Y = 1; if(Z == 0) Z = 1; int a = Euclid(X, Y*Z); return Combine((x*1.0/a)/(Y*Z/a));//强转或x*1.0,否则返回int } //计算概率 private static double binomial(int N, int k, double p){ double p1 = 1; double p2 = 1; for(int i = 1; i <= k; i++){ p1 *= p; } for(int i = 1; i <= (N-k); i++){ p2 *= 1-p; } double C = Combine(N, k, N-k); return C * p1 * p2; } public static void main(String[] args){ System.out.println(binomial(100, 50, 0.25)); //概率:6.828252801404798E-91 }}
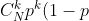 ^{N-k}=(1-p)CN^{k-1}p^k(1-p)^{N-k-1}&space;+&space;pC{N-1}^{k-1}p^{k-1}(1-p)^{N-k}#)^{N-k}=(1-p)CN^{k-1}p^k(1-p)^{N-k-1}&space;+&space;pC{N-1}^{k-1}p^{k-1}(1-p)^{N-k})">binomial方法主要运用了二项概率的递推公式
^{N-k}=(1-p)CN^{k-1}p^k(1-p)^{N-k-1}&space;+&space;pC{N-1}^{k-1}p^{k-1}(1-p)^{N-k}#)^{N-k}=(1-p)CN^{k-1}p^k(1-p)^{N-k-1}&space;+&space;pC{N-1}^{k-1}p^{k-1}(1-p)^{N-k})">binomial方法主要运用了二项概率的递推公式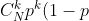 ^{N-k}=(1-p)CN^{k-1}p^k(1-p)^{N-k-1}&space;+&space;pC{N-1}^{k-1}p^{k-1}(1-p)^{N-k}#)^{N-k}=(1-p)CN^{k-1}p^k(1-p)^{N-k-1}&space;+&space;pC{N-1}^{k-1}p^{k-1}(1-p)^{N-k})
^{N-k}=(1-p)CN^{k-1}p^k(1-p)^{N-k-1}&space;+&space;pC{N-1}^{k-1}p^{k-1}(1-p)^{N-k}#)^{N-k}=(1-p)CN^{k-1}p^k(1-p)^{N-k-1}&space;+&space;pC{N-1}^{k-1}p^{k-1}(1-p)^{N-k})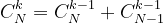 ">约分即得到组合数递推公式
">约分即得到组合数递推公式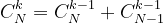
^{N-k}=(1-p)CN^{k-1}p^k(1-p)^{N-k-1}&space;+&space;pC{N-1}^{k-1}p^{k-1}(1-p)^{N-k}#)^{N-k}=(1-p)CN^{k-1}p^k(1-p)^{N-k-1}&space;+&space;pC{N-1}^{k-1}p^{k-1}(1-p)^{N-k})
=C_N^kp^k(1-p)^{N-k}#)
!}#)