1. 关于检索

检索(search)：在一组记录中找到某个具有关键码值的记录，或者找到关键码值符合某些条件的一些记录。

常见算法

常见的检索算法分为三类

  1. 顺序表和线性表方法
  2. 根据关键码值直接访问的方法（Hash）
  3. 树索引

    评价指标

    对线性表检索算法常采用ASL（average searching length，平均检索长度）进行评价，它表示查找若干记录的平均关键字比较次数。 :::info 判断元素K是否在长为n的线性表L中：令pi为K在L中位置i的几率（下标为0~n-1的某处），对于任意位置i处值必须查看i+1条记录来访问；当K不在L中时，需要比较n次才能确认**，设pn为K不在L的几率，则ASL可以表示为
    Ch9 检索（Searching） - 图1
    假设除了pn外的每个pi相等
    Ch9 检索（Searching） - 图2 :::

2. 检索线性表

  • 未排序线性表：根据👆推导，检索无序线性表开销为O（n）
  • 顺序线性表：通常采取二分法检索，开销O（logn）

3. 自组织线性表

完全根据关键值排序的线性表开销较大，一般也可以按照请求频率组织线性表，在有限开销情况下提高检索效率。主要有以下三种规则进行组织

  • count（计数法）：为每个记录添加一个访问计数，每次访问则计数+1，该记录前移，直到遇到另外一个计数更大的，最终所有记录根据访问计数顺序排列；
  • move-to-front（移至最前端）：找到一条记录后，该记录移动到最前端，易使用链表实现，类似LRU算法
  • transpose（转置）：找到一条记录后与其前一记录交换 :::info 举例：给定线性表ABCDEFG，访问FDFG，使用以上三种规则时的线性表变换图示如下：
    ① count
    Ch9 检索（Searching） - 图3


② move-to-front
Ch9 检索（Searching） - 图4

③ transpose
Ch9 检索（Searching） - 图5 :::

4. 哈希表⭐

概述

通过一些计算，把关键值映射到数组中的位置来访问记录，这个过程称为散列（hashing）；

  • 把关键值映射到位置的函数称为散列函数（hash function， h），向哈希表中插入\检索\删除记录都与之相关；
  • 存放记录的数组叫做散列表（hash table， HT）；HT中一个位置叫做一个槽（slot），HT中slot总数为M，slot从0编号到M-1；

设计散列系统的意义是使得对任何关键码值K和某个散列函数h，i=h(K)是表中满足0<=h(K)<M的一个slot，且记录在HT[i]存储的关键码值等于K

哈希函数

根据上述要求，哈希函数的构造原则如下

  1. MUST：返回一个值，不超过HT索引范围（0~M-1）
  2. SHOULD：尽可能使得码值均匀分布至表中空位

常见哈希函数

  1. 除留余数法：Ch9 检索（Searching） - 图6

    1. // 举例，此时M=16
    2. int h(int x){
    3.  return x % 16
    4. }

  2. 平方取中法：计算key，取中间r位作为h(k)返回值，下图说明了结果中的哪些位收到操作数的影响更大，可以发现57是受所有位置操作数影响的，此时使用这两位可以使得key分布更均匀

    Ch9 检索（Searching） - 图7

  3. 折叠法：把所有字符串字符ASCII码值累加对M取模，适合key是字符串且sum>>M

5. 哈希冲突与解决

当key1≠key2，但是h(key1)=h(key2)，此时插入记录时会产生表内冲突（collisions），常见解决思路**

  1. closed hashing：闭域法/开放地址法（冲突放入另一个slot）

  2. open hashing：开域法/链地址法（冲突存入链表）

    闭域法/开放地址法

    所有记录存在一张表内，为每个记录求得一个探查序列（probe sequence）Ch9 检索（Searching） - 图8，其中Ch9 检索（Searching） - 图9如果产生冲突则增加偏移重新取模Ch9 检索（Searching） - 图10其中di的值取决于探查函数Ch9 检索（Searching） - 图11，常见有如下探查函数

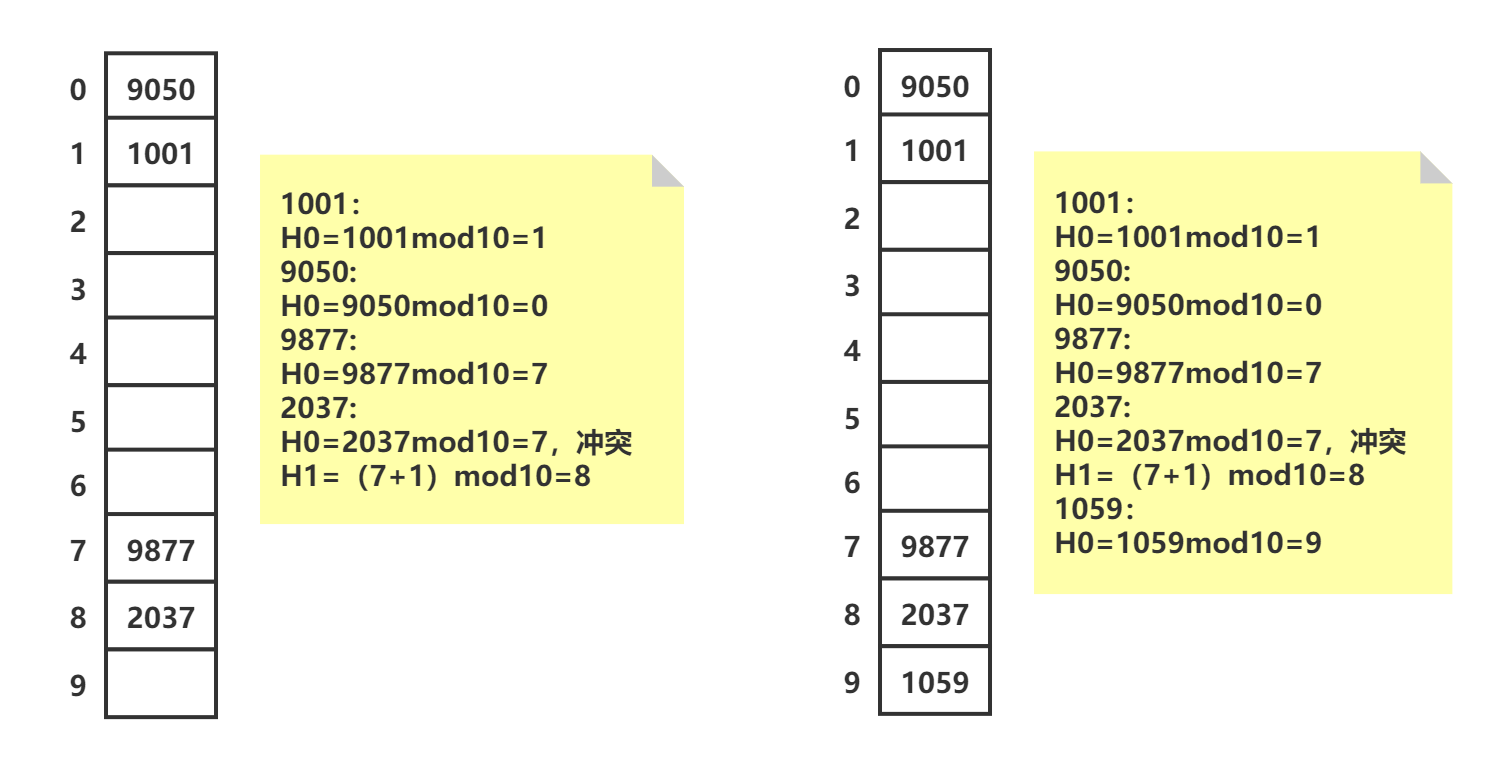
  3. 线性探查：Ch9 检索（Searching） - 图12 :::info 线性探查.png
    上图图示了线性探查，该函数的缺点是容易导致记录聚集到一起，把这种倾向叫做基本聚集（primary clustering），它会产生很长的探查序列：理想情况下每个slot有相同几率接受记录，但实际上每插入一个记录，其余空槽被填充的几率都会改变，图示左侧slot2，slot9被填充几率实际上是3/10，当slot9被填充后，slot2被填充几率会变成6/10 :::

  4. 二次探查：Ch9 检索（Searching） - 图14

线性探查使得基本聚集产生了很长的探查序列，因为每次冲突后的Hi都是连续的，为此我们可以“跳着走” :::info 例题：已知M=10，h(k)=k%11，采用二次探查，作用于关键值：19，1，23，14，55，68，11，82，36，并计算放入剩下slot的概率
二次探查.png
Ch9 检索（Searching） - 图16
此时下个位置情况
Ch9 检索（Searching） - 图17 :::

  1. 随机探查：(伪)随机取值


双哈希

需要注意的是，二次探查和随即探查虽然可以消除基本聚集，但还有另一个问题—**“二次聚集”**：把H0位置记作基槽，如果两个key被散列到一个基槽，其后的探查序列依旧会重复。这是因为此后Ch9 检索（Searching） - 图18下一个slot与K无关只和H0有关，因此为了解决二次聚集，我们需要使用二次散列方法（双哈希），再采用额外的一个哈希函数h2
Ch9 检索（Searching） - 图19

:::info 例题：已知M=11，关键值序列{19，1，23，12，55，68，24，86，35}，h(k)=k%11，采用线性探查+双哈希，Ch9 检索（Searching） - 图20，求最终序列
解：
Ch9 检索（Searching） - 图21 双哈希.png :::

开域法/链地址法

将hash地址相同的记录链接在同一链表中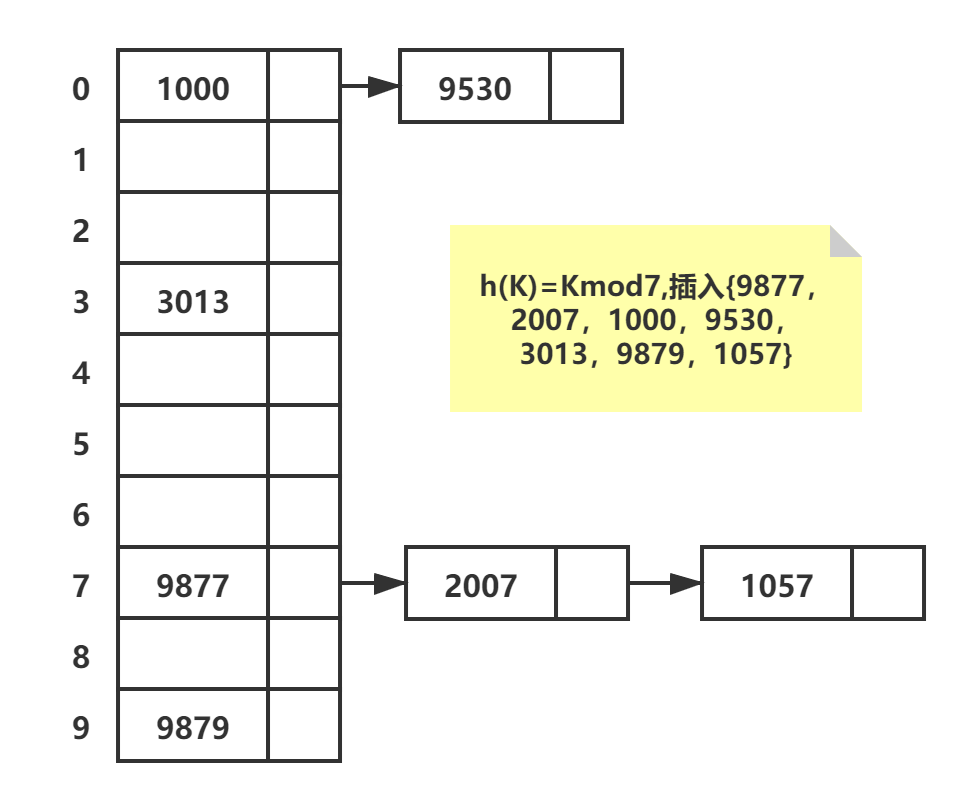
开散列.png

6. 哈希表操作

检索

  1. 对key，求H0，H1 …
  2. i=0开始，若key=HT[Hi]则查找成功，否则检索Hi+1

决定在哈希表中检索ASL的因素

  1. 哈希函数
  2. 冲突解决方法
  3. 哈希表饱和程度：装载因子：Ch9 检索（Searching） - 图24，哈希表操作的时间开销都和饱和程度成正比，越饱和开销越大

每次散列方法的时间开销接近于一次访问，因此检索/插入/删除的时间开销为O(1)，空间开销为O(n)

删除

  1. 删除不能影响后续检索
  2. 不希望某个位置由于删除记录而不可用：通常使用tombstone，在删除处设置标记，表示不再占用，但也不会使得检索中断