最小生成树MST API

public class MST

返回类型 方法 描述
MST(EdgeWeightedGraph G) 构造函数
Iterable edges() MST所有边
double weight() MST权重

Prim算法

  • 描述:每一步为树添加一个边.开始树只有一个顶点,向其中添加V-1条边,每次从连接树中顶点和树补的边中选择权重最小的边
  • 命题:Prim算法可以得到任意加权连通图的最小生成树

证明:即切分定理

  • 数据结构:
    • 顶点:使用boolean marked[],当顶点v在树中,marked[v]==true
    • 边:Queue mst,保存MST中的边
    • 横切边:使用优先队列MinPQ根据权重比较所有边
      • 边的失效:当marked[v]&&marked[w]时,这样的边已经非横切边,即失效

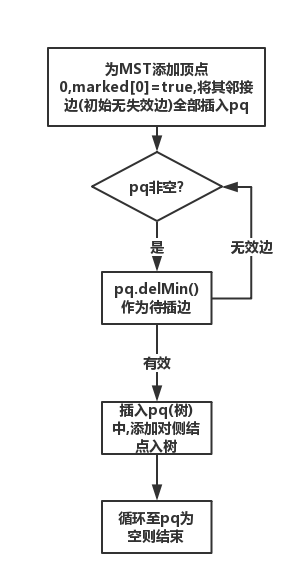
实现1.延时实现

  • 延时实现:无效边留在优先队列pq当中,delMin()时判断,跳过无效边
  • 注意:LazyPrimMST的pq非即时删除无效边,则运行中pq的元素数会超过G.V(),因此MinPQ需要resize()

LazyPrim.jpg

  1. import edu.princeton.cs.algs4.In;
  2. import edu.princeton.cs.algs4.StdOut;
  4. public class LazyPrimMST {
  5.     private boolean[] marked;//树中顶点
  6.     private Queue<Edge> mst;//树中边
  7.     private MinPQ<Edge> pq;//横切边(含无效边)
  9.     public LazyPrimMST(EdgeWeightedGraph G){
  10.         marked = new boolean[G.V()];
  11.         mst = new Queue<>();
  12.         pq = new MinPQ<>(G.V());
  14.         visit(G,0);
  15.         while (!pq.isEmpty()){
  16.             Edge e = pq.delMin();//最小权边(可能无效)
  17.             int v = e.either(), w = e.other(v);
  18.             if (marked[v] && marked[w]) continue;
  19.             mst.enqueue(e);
  20.             if (!marked[w]) visit(G,w);//将v或w加入树中(另一个已经在树中)
  21.             if (!marked[v]) visit(G,v);
  22.         }
  23.     }
  25.     //标记入树函数
  26.     private void visit(EdgeWeightedGraph G, int v){
  27.         marked[v] = true;
  28.         for (Edge e: G.adj(v))
  29.             if (!marked[e.other(v)]) pq.insert(e);
  30.     }
  32.     public Iterable<Edge> edges(){ return mst;}
  34.     public static void main(String[] args){
  35.         In in = new In(args[0]);
  36.         EdgeWeightedGraph G = new EdgeWeightedGraph(in);
  38.         LazyPrimMST mst = new LazyPrimMST(G);
  39.         for (Edge e:mst.edges())
  40.             StdOut.println(e);
  41.     }
  42. }

算法分析

  • 命题:LazyPrim计算连通加权无向图G(V,E)的最小生成树所需空间和E成正比,时间和ElogE(最坏)成正比

证明:优先队列的insert()和delMin()中的比较是主要考虑部分.优先队列中E条边,即空间上限,最坏情况下,insert()为~lgE,delMin()为2lgE,因为最多只能插入E条边,删除E次最小元素.则最坏为ElogE(优先队列)

实现2.即时实现

  • 即时实现:在pq中实时的删去无效边,只在pq中保存每个非树顶点w的一条边:即已知将其与树中点连接的最小权重边
  • PrimMST使用索引优先队列,edgeTo[]和distTo[],具有以下性质
    • marked[i],i在树中
    • pq为索引优先队列,delMin()返回indexOfMin,即返回最小横切边关联的结点
    • edgeTo[v]是v与树相连的权最小边,distTo[v]即权值
  1. public class PrimMST {
  2.     private Edge[] edgeTo;//距树最近(最小权)边
  3.     private double[] distTo;//最小权
  4.     private boolean[] marked;//树中点
  5.     private IndexMinPQ<Double> pq;//有效横切边
  7.     public PrimMST(EdgeWeightedGraph G){
  8.         edgeTo = new Edge[G.V()];
  9.         distTo = new double[G.V()];
  10.         marked = new boolean[G.V()];
  11.         for (int v = 0; v < G.V(); v++)
  12.             distTo[v] = Double.POSITIVE_INFINITY;//权值都初始为正无穷
  13.         pq = new IndexMinPQ<>(G.V());
  14.         distTo[0] = 0.0;//顶点0和0.0初始化起点
  15.         pq.insert(0,0.0);
  16.         while (!pq.isEmpty())
  17.             visit(G,pq.delMin());
  18.     }
  20.     private void visit(EdgeWeightedGraph G, int v){
  21.         marked[v] = true;
  22.         for (Edge e:G.adj(v)){
  23.             int w = e.other(v);
  24.             if (marked[w]) continue;//忽略失效边v-w
  25.             if(e.weight() < distTo[w]){//发现更短有效路径e
  26.                 edgeTo[w] = e;
  27.                 distTo[w] = e.weight();
  28.                 if (pq.contains(w)) pq.change(w, distTo[w]);//非首次加入树
  29.                 else pq.insert(w,distTo[w]);//首次加入树
  30.             }
  31.         }
  32.     }
  34.     public Iterable<Edge> edges(){
  35.         Bag<Edge> mst = new Bag<>();
  36.         for (int v = 1; v < edgeTo.length; v++)
  37.             mst.add(edgeTo[v]);
  38.         return mst;
  39.     }
  40. }

算法分析

  • 命题:Prim算法计算连通加权无向图G(V,E)的最小生成树所需空间和V成正比,时间和ElogV(最坏)成正比

证明:pq中顶点数最多为V,使用三个索引数组,则空间上限和V成正比.已知基于堆的索引优先队列的操作增长数量级是logV,则相加总时间和ElogV成正比

图示
PrimMST.jpg