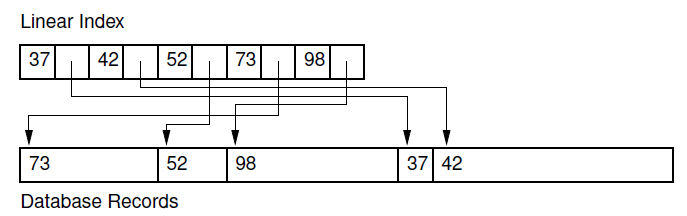
:::danger 检索(searching)与索引(indexing)

  • 索引有两重意思：作为动词指的是关联一个关键值key和与其相关数据的过程，作为名词就是为了上述过程后所得的索引文件
    • 如下方的B树，B+树等都是索引文件，建树过程可以称为索引过程
  • 检索则是根据索引文件使用key找到其相关的数据
    • 数组的下标可视为其索引，而使用下标访问a[i]就是检索过程
    • Ch9中的散列虽然被放在检索部分，但它也是一种索引，key是value本身的映射关系 :::

      1. 线性索引

      image.png
      线性索引文件被组织成关键值或者指针对的形式，特性如下：
  1. 适于索引输入顺序文件(entry-sequenced file)
  2. 适用二分法搜索
  3. 适用变长记录
  4. 对于静态数据库更高效

缺点：当数据库频繁的插入/删除记录时，索引文件需要更新，开销较大

2. 2-3树

定义

image.png
2-3树是一种树状结构，其需要满足以下特性

  1. 每一个结点包含1或2个key值
  2. 每个内部节点有2或3个子结点
  3. 所有叶子结点都在树结构的同一层，因此高度平衡
  4. 结点大小关系：
    1. 左子树所有结点值都小于第一个码；
    2. 中间子树所有结点值大于等于第一个码；
    3. 右子树所有结点都大于等于第二个码；

      操作

      以下操作开销都为O(logn)
检索 2-3树检索只需依据key值大小深入子树即可，可参考BST的findhelp()
插入
1. 找到合适的叶子结点L
1. L已有一个值时，填入key到左/右位置，保持左小右大
1. L有两个个值时
1. spilt():将L分为L和L’，L放置三者中最小的，L’放三者最大的值
1. promotion():将中间值提升到父结点
1. 若父结点只有一个值，处理方法同2
1. 若父结点有两个值，处理方法同3**

构造

见下方B树构造，与BST从上至下构造不同，2-3T从下至上构造 :::info 举例：给定的keys为C，S，D，T，A，M，P，I构造2-3树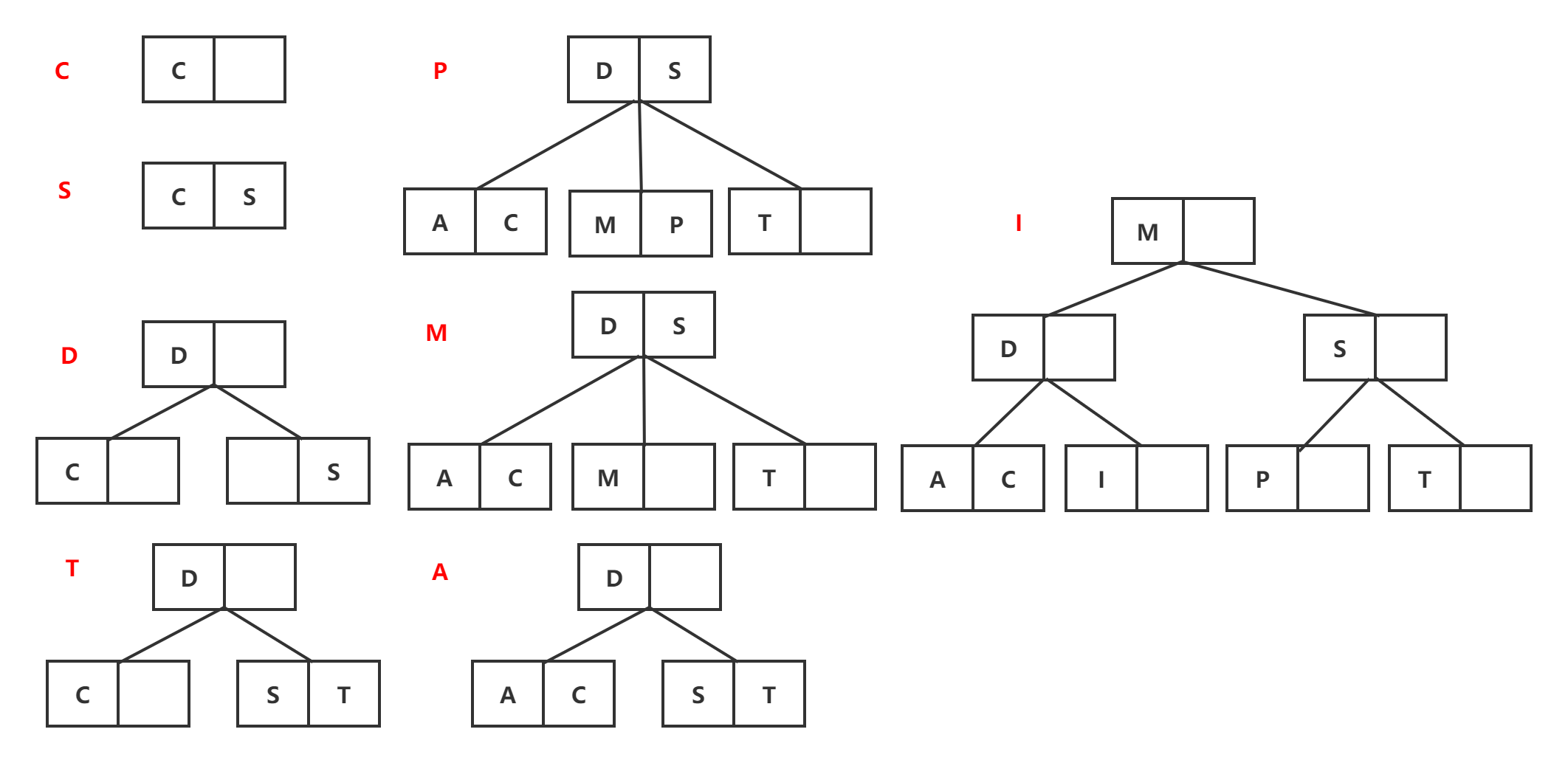
2-3树.png :::

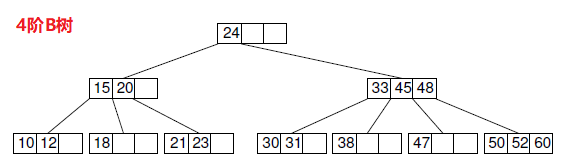
3. B树

B树可以有效处理基于磁盘的检索问题

定义

image.png
Ch10 索引（Indexing） - 图5

构造

Ch10 索引（Indexing） - 图6

操作

Ch10 索引（Indexing） - 图7 :::danger 我们画图时忽略了B树每个节点实际都是键值对，默认只关注了key是因为key才是构造与检索时需要的，但是这点仍需要注意
可以参考Node的实现：TTNode.java :::

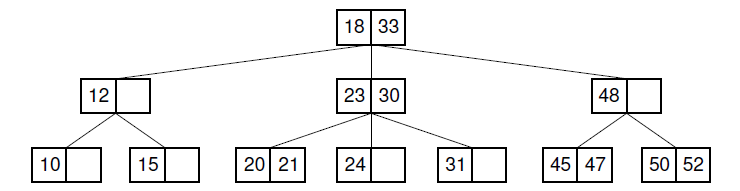
4. B树

定义

image.png
Ch10 索引（Indexing） - 图9

构造

除了需要满足上面的特性外还需要确定

  • n：叶子结点可保存的最多n个记录数
  • m：内部结点最多m-1个键值

    操作

    以下操作开销都为O(logn)
检索
- 不同于其他数据结构,B+树可以从root开始根据key检索(树查找),也可以直接访问叶子结点链表顺序查找
- 树查找时无论查找是否成功,必须抵达叶子结点
插入
1. 找到合适的叶子结点L
1. L已有一个值时，填入key到左/右位置，保持左小右大
1. L有两个个值时
1. spilt():将L分为L和L’，将key插入
1. promotion():将右半L’中最小记录副本提升到父结点
1. 若父结点只有一个值，处理方法同2
1. 若父结点有两个值，处理方法同3**
删除

总结
Ch10 索引（Indexing） - 图10

:::info 以下图B+树为初始树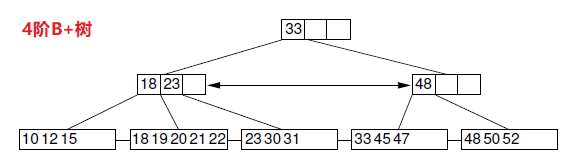Ch10 索引（Indexing） - 图11
image.png
(1)初始树依次删除18，19，20的结果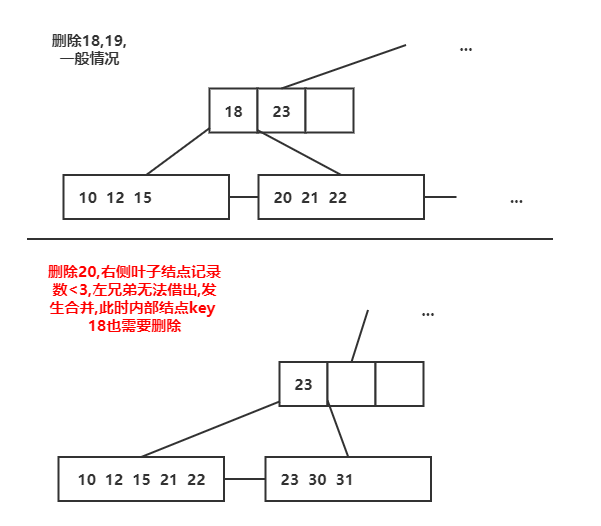
B+T(1).png
(2)初始树插入9，14，17，再删除50的结果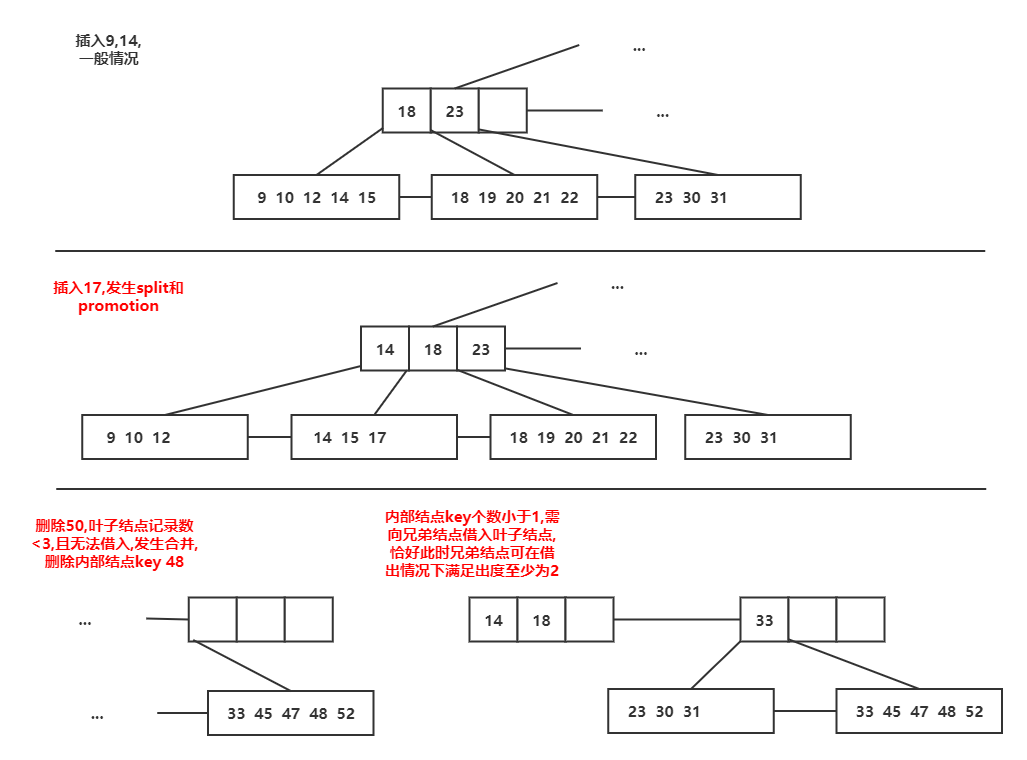
B+T(2).png :::