背景

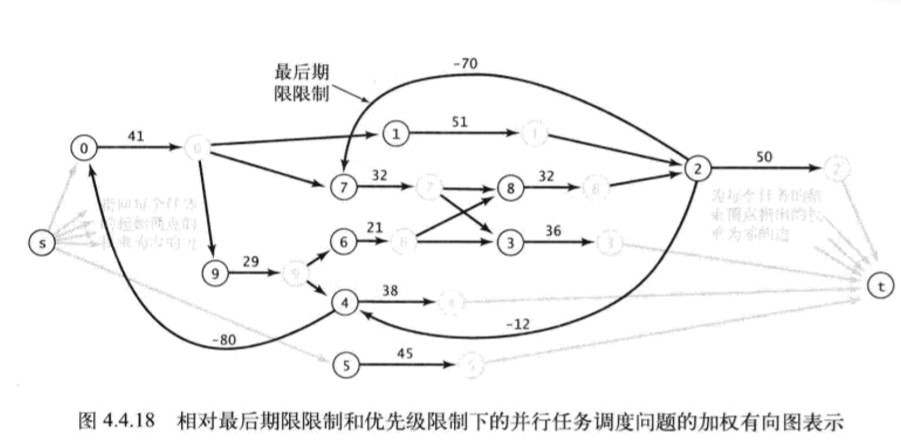
  • 问题:相对最后期限限制的并行任务调度:算法4.10中,优先级限定的并行任务处理转化为加权有向无环图副本(权重都取相反数)的最短路径/原图的最长路径问题,但现在若限定了两个任务间的期限限制
    • 建模:此时问题转换为一个可能存在环和负权重边的加权有向图最长路径/副本最短路径问题:v必须在w启动后d时间开始,则添加v->w,权重为-d的边
      • 如2必须在4开始后12个单位时间开始,则2的开始点->4的开始点产生一条权重-12的边
    • 正确性证明:Topo顺序放松保证了优先级限制,v->w的负权值在放松v时表现为(distTo[])timeToDo[w]<timeToDo[v]-d进一步d<timeToDo[v]-timeToDo[w]即相对期限

deadline.jpg

准备:关于一般加权有向图的最短路径问题

对比

  • 权值都非负:重点在找寻近路
  • 负权重:重点在为了经过负权重道路,甚至绕弯
  • 可知算法的本质不在于找寻近路

常见误区

  1. 找到最小负权值-d,给每条边加上|-d|,产生一个无负权图,从中找最短路径

错误:产生的新图最短路径和原图无关,间上述对比

  1. 对Dijkstra算法修改

错误:Dijkstra算法的前提在于distTo[w]只会变大,但现在前提不成立,算法不成立

负权重的环

  • 负权重环是一个还上边的权重和为负的环
  • 当且仅当s到v的有向路径任何点不在负权重环内,s到v的最短路径才有意义

证明:若存在负权重环,则一直绕着环就可以使得路径无限变短

问题解决的前提

  • s不可达的顶点,distTo[]设为+∞
  • s到可达点路径上属于负权重环的顶点,distTo[]设为-∞
  • 对其余顶点,计算最短路径
  • 因此,在一般有向图中监测负权重环,在其不可达时解决最短路径问题

算法4.11 基于队列的Bellman-Ford算法

  • Bellman-Ford算法:任意含有V顶点的加权有向图限定起点s,从s无法达任何负权重环:将distTo[s]初始化为0,其余为+∞,以任意顺序放松有向图所有边,重复V轮

证明:归纳法,假设进行V轮
i=0,1显然成立
设i时成立
当进行i+1轮放松时,distTo[v]=distTo[v]+e.weight(),不会更大,因为第i轮放松保证了最短路径;不会更小,它本身就是最短路径

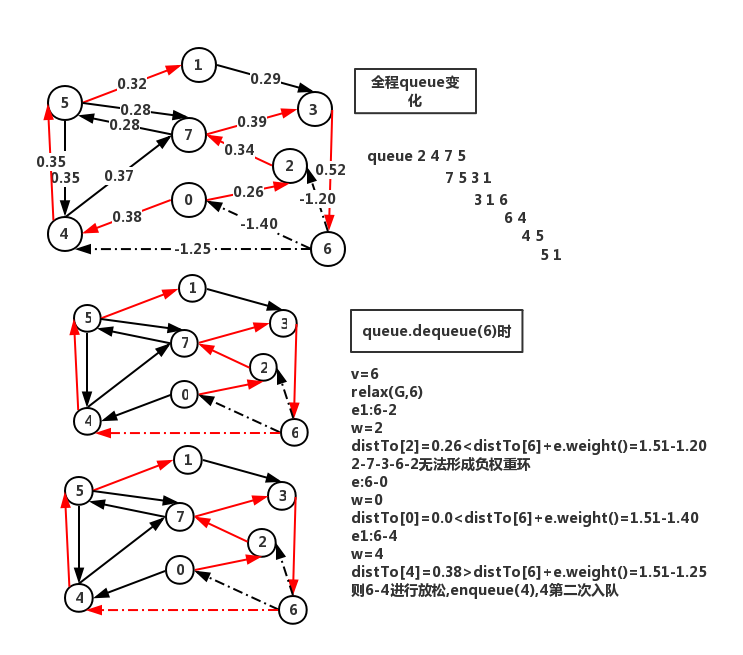
改进:基于队列的Bellman-Ford算法

  • 每一轮放松时只有上一轮distTo[]变化的顶点出边才会对其他distTo[]有影响,因此选用队列保存这样的顶点再进行放松

数据结构

  • queue:保存上一轮distTo[w]变化的w
  • boolean[] onQ:指示顶点是否已经在队列中,防止重复入队

relax()

  1. private void relax(EdgeWeightedDigraph G, int v){
  2.     for (DirectedEdge e: G.adj(v)){
  3.         int w = e.to();
  4.         if (distTo[w] > distTo[v]+e.weight()){
  5.             distTo[w] = distTo[v]+e.weight();
  6.             edgeTo[w] = e;
  7.             if (!onQ[w]){
  8.                 queue.enqueue(w);
  9.                 onQ[w] = true;
  10.             }
  11.         }
  12.         //每次放松完一个顶点后查找是否到达一个负权重环
  13.         if (cost++ % G.V() == 0) 
  14.             findNegativeCycle();
  15.     }
  16. }

实现

  1. public class BellmanFordSP {
  2.     private double[] distTo;
  3.     private DirectedEdge[] edgeTo;
  4.     private boolean[] onQ;//顶点是否在队列中
  5.     private Queue<Integer> queue;//正被放松的顶点
  6.     private int cost;//relax()调用次数
  7.     private Iterable<DirectedEdge> cycle;//edgeTo[]中是否有负权重环
  9.     public BellmanFordSP(EdgeWeightedDigraph G, int s){
  10.         distTo = new double[G.V()];
  11.         edgeTo = new DirectedEdge[G.V()];
  12.         onQ = new boolean[G.V()];
  13.         queue = new Queue<>();
  14.         for (int v = 0; v < G.V(); v++)
  15.             distTo[v] = Double.POSITIVE_INFINITY;
  16.         distTo[s] = 0.0;
  17.         onQ[s] = true;
  18.         while (!queue.isEmpty() && !hasNegativeCycle()){
  19.             int v = queue.dequeue();
  20.             onQ[v] = false;
  21.             relax(G, v);
  22.         }
  23.     }
  25.     private void relax(EdgeWeightedDigraph G, int v){}
  27.     public double distTo(int v){}
  28.     public boolean hasPathTo(int v){}
  29.     public Iterable<DirectedEdge> pathTo(int v){}
  31.     private void findNegativeCycle(){ }
  32.     private boolean hasNegativeCycle(){ }
  33.     public Iterable<Edge> negativeCycle(){ }
  34. }

Bellman.png

算法分析

  • V个顶点的加权有向图给定起点s,最坏情况时间和EV成正比,空间和V成正比

    证明:每一轮放松E条边,共V轮

负权重环的监测

  • 参考4.2节有向环寻找类DirectedCycle构造EdgeWeightedDirectedCycle
  1. private void findNegativeCycle(){
  2.         int V = edgeTo.length;
  3.         EdgeWeightedDigraph spt;
  4.         spt = new EdgeWeightedDigraph(V);
  5.         for (int v = 0; v < V; v++){
  6.             if (edgeTo[v] != null)
  7.                 spt.addEdge(edgeTo[v]);
  8.         }
  10.         EdgeWeightedDirectedCycle cf;
  11.         cf = new EdgeWeightedDirectedCycle(spt);
  12.         cycle = cf.cycle();    
  13.     }
  14. private boolean hasNegativeCycle(){ return cycle!=null;}
  15. public Iterable<DirectedEdge> negativeCycle(){ return cycle;}

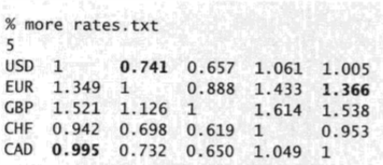
套汇问题

  • 背景:给定一个sxt货币兑换图,(s,t)处数字即为1单位货币s可兑换多少货币t
    • 问题:表格等价于加权有向图,顶点:货币,边和权重:货币对以及汇率,若s->t权重x,t->u权重y,则s->t->u即1单位货币s可兑换xy个货币t,但当u->s权重z且xyz>1时,表面s->t->u->s可以用1单位s换取大于1单位s,套汇即以钱生钱
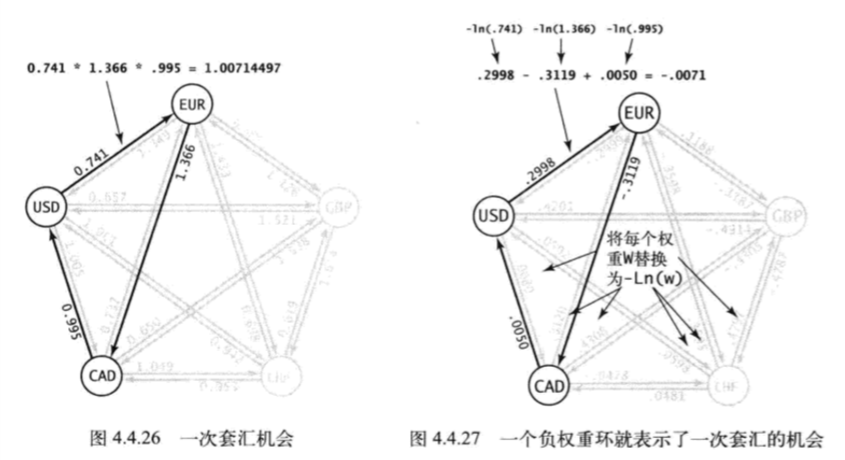
      • 建模:套汇问题即有向加权图的负权重环检测问题
      • 证明:将汇率取对数后取反,如-ln(0.74),这样汇率之积xyz对应-ln(x)-ln(y)-ln(z)之和,xyz>1对应-ln(x)-ln(y)-ln(z)<0,即负权重环代表一种套汇机会

Arbitrage1.png
Arbitrage2.png