例题1:二维离散

生物群体t=0时只有一个个体,t=1时要么分裂为两个独立个体,要么死亡;t=2时两个个体独立演化.假设分裂与死亡概率同为1/2,X,Y分别表示t=1和t=2时个体数,则: (1) t=2时,群体灭绝概率(Y=0) (2) t=2时群体灭绝的条件下,求t=1时未灭绝概率 (3) 求(X,Y)概率分布 (4) 求X,Y的边缘分布,判断是否独立

:::info

  1. Ch3 例题 - 图1
  1. Ch3 例题 - 图2
  1. Ch3 例题 - 图3
  1. Ch3 例题 - 图4 :::

例题2:二维连续+边缘分布+条件分布

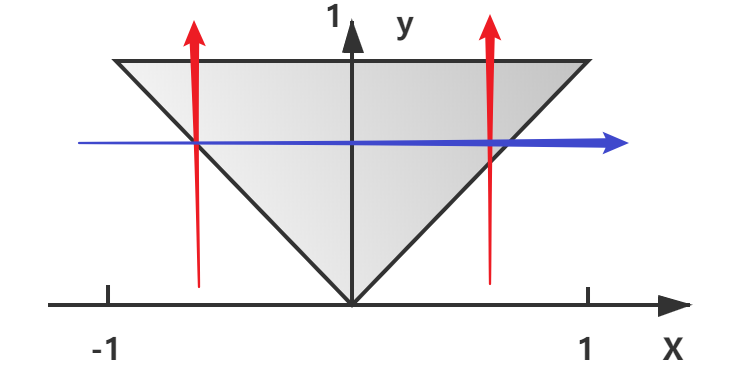
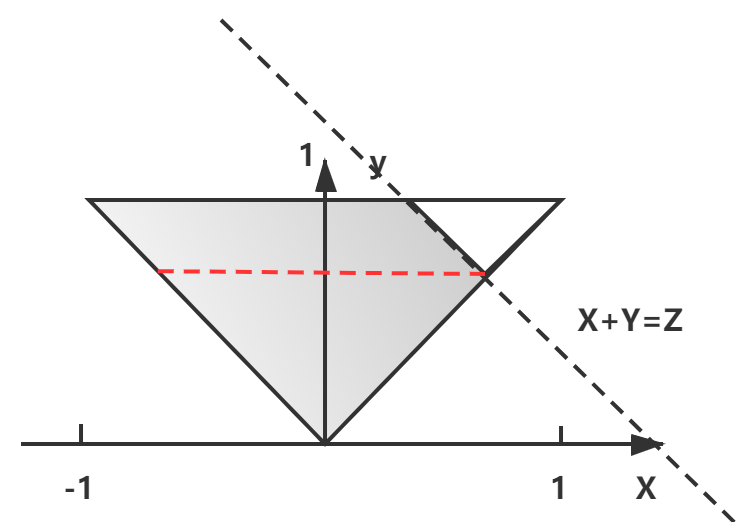
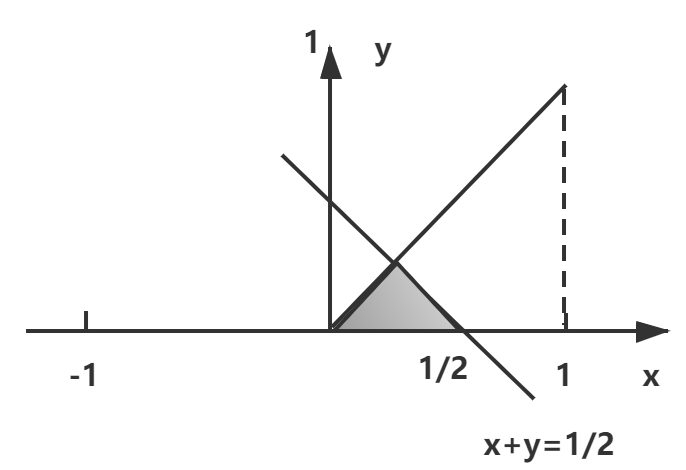
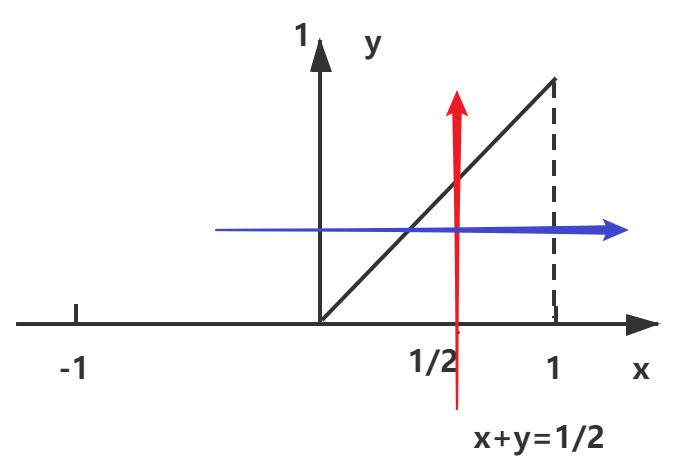
设G(X,Y)为G上的均匀分布,G={(X,Y)|0≤y≤1,-y≤x≤y} (1) 求XY的边缘密度函数Ch3 例题 - 图5,并判断独立性 (2) 求Ch3 例题 - 图6 (3) 若Z=X+Y,求Z的密度函数Ch3 例题 - 图7

:::info

  1. Ch3 例题 - 图8 例2(1).png
  1. Ch3 例题 - 图10

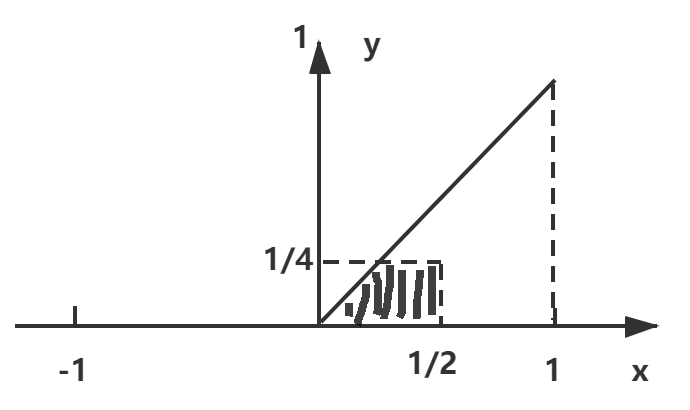
不同于一重积分,在二重积分中,画图只是为了确定积分上下限,此图像的面积和积分结果无关

  1. Ch3 例题 - 图11 例2(3).png
    1.                       :::

例题3:二维连续+边缘分布+条件分布

已知Ch3 例题 - 图13 (1) 求A (2) 求Ch3 例题 - 图14 (3) 求Ch3 例题 - 图15 (4) 求Ch3 例题 - 图16 (5) 求Ch3 例题 - 图17

:::info

  1. Ch3 例题 - 图18
  1. Ch3 例题 - 图19 例3(2).png
  1. Ch3 例题 - 图21 例3(3).png
  1. Ch3 例题 - 图23Ch3 例题 - 图24 例3(4).png
  1. Ch3 例题 - 图26Ch3 例题 - 图27
    :::