Ch5 二叉树

1. 概述

定义和性质

二叉树是n个有限元素(结点，nodes)的集合，该集合要么为空，要么由一个根元素**(root)**及两个不相交的左，右子树(同为二叉树)组成，是有序树.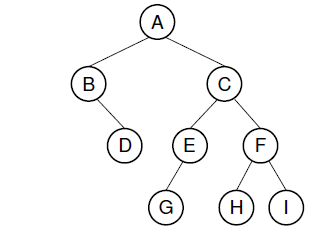

• 高度&深度

每个二叉树有以下属性

• 满&完全

根据二叉树形态可以分为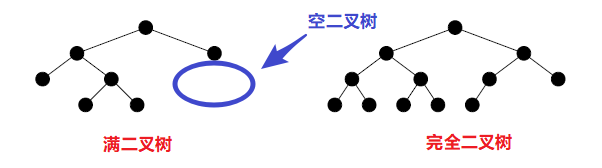

• 结构性开销

有关定理

2. 遍历

根据树/子树根结点被访问的顺序可以分为三种二叉树遍历方法：以图中二叉树为例，三种对应遍历序列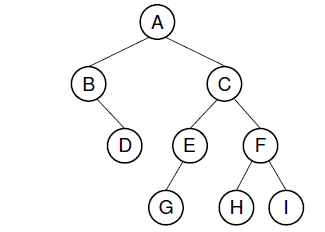

:::info 讨论已知前/中/后序遍历结果中的几个可确定唯一二叉树

• 已知(前+中)或(后+中)：可确定唯一二叉树，因为可确定根结点与子树
• 已知(前+后)：不可确定唯一二叉树
  :::

3. 数组实现CBT

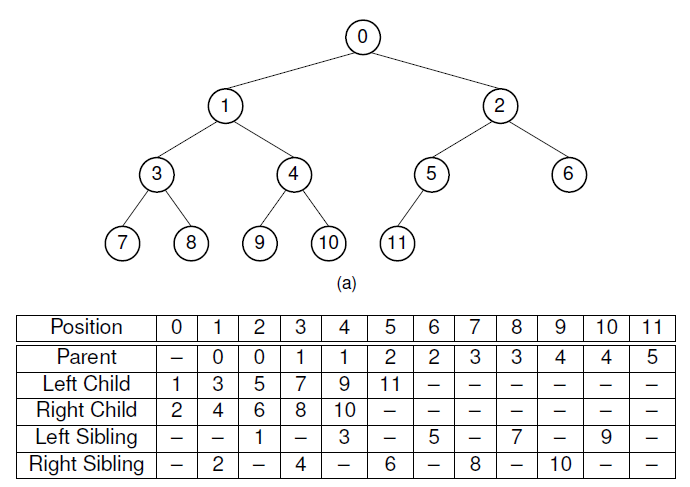
4. 二叉检索树(BST)

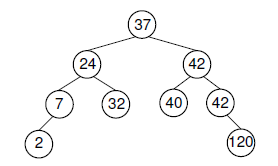
对任意一个结点，其左子树任意结点值都<k，右子树任意结点值≥k

| 当我们要检索一个值k,从根结点开始
- root值=k,检索jies
- root值>k,进入左子树检索
- root值 👉右图,若要检索32:
- 37>32进入左子树
- 24<32进入右子树
- 32=32检索成功
| ** | | —- | :—-: |

实现

BST.java

方法详解

• findhelp

检索，对比当前结点key和检索值k，再深入左右子树
时间开销：Θ(log**2n)~Θ(**n)，取决于平衡性(左右子树规模)

private E findhelp(BSTNode<Key, E> rt, Key k)
{
    if (rt == null)
        return null;
    if (rt.key().compareTo(k) > 0)
        return findhelp(rt.left(), k);
    else if (rt.key().compareTo(k) == 0)
        return rt.element();
    else
        return findhelp(rt.right(), k);
}

• inserthelp

插入新结点，类似检索过程，找到合适的位置后插入为新的叶结点
时间开销：Θ(log**2n)~Θ(**n)，取决于平衡性

private BSTNode<Key, E> inserthelp(BSTNode<Key, E> rt, Key k, E e)
{
    if (rt == null)
        return new BSTNode<Key, E>(k, e);
    if (rt.key().compareTo(k) > 0)
        rt.setLeft(inserthelp(rt.left(), k, e));
    else
        rt.setRight(inserthelp(rt.right(), k, e));
    return rt;
}

• deletemin/getmin

删除/获取当前树中最小的key，即一路沿左侧枝杈找到末端叶结点

private BSTNode<Key, E> deletemin(BSTNode<Key, E> rt)
{
    if (rt.left() == null)
        return rt.right();
    rt.setLeft(deletemin(rt.left()));
    return rt;
}
private BSTNode<Key, E> getmin(BSTNode<Key, E> rt)
{
    if (rt.left() == null)
        return rt;
    return getmin(rt.left());
}

• removehelp

删除指定的X结点，分情况(见下图)：

1. X只有LC，则：X.LC变成X.parent的LC
2. X只有RC，则：X.RC变成X.parent的RC
3. X兼具LC，RC，则：X右子树最小值变成X.parent

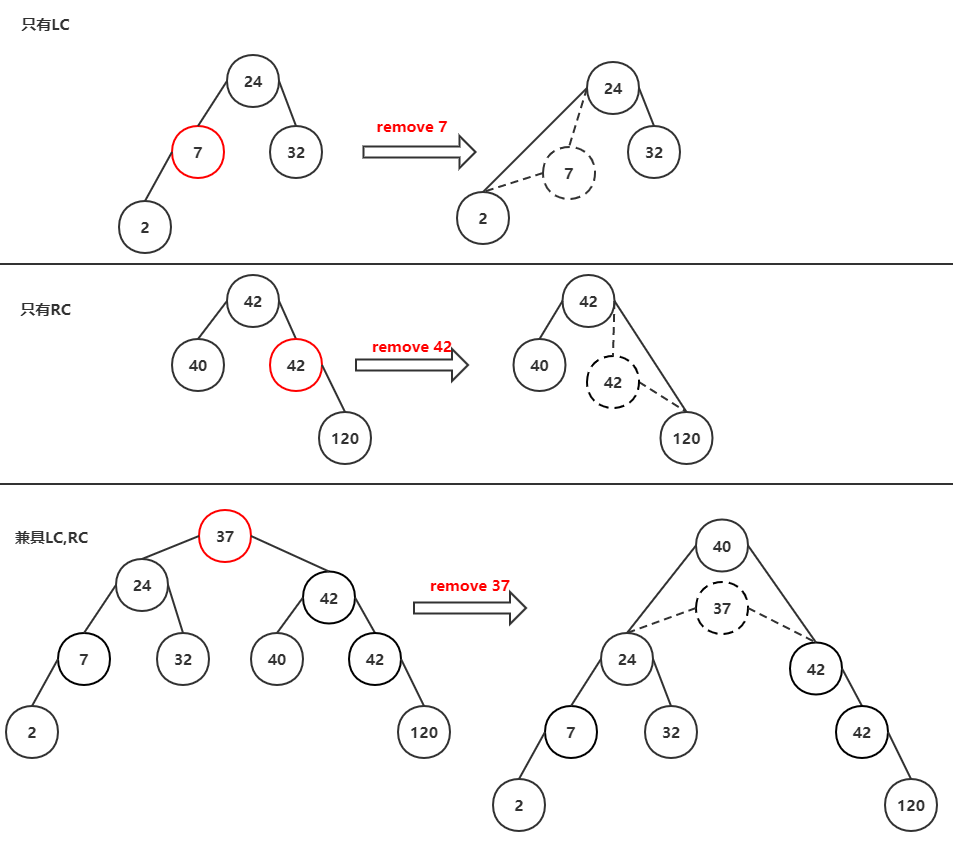
private BSTNode<Key, E> removehelp(BSTNode<Key, E> rt, Key k)
{
    if (rt == null)
        return null;
    if (rt.key().compareTo(k) > 0)
        rt.setLeft(removehelp(rt.left(), k));
    else if (rt.key().compareTo(k) < 0)
        rt.setRight(removehelp(rt.right(), k));
    else
    { // Found it
        if (rt.left() == null)
            return rt.right();
        else if (rt.right() == null)
            return rt.left();
        else
        { // Two children
            BSTNode<Key, E> temp = getmin(rt.right());
            rt.setElement(temp.element());
            rt.setKey(temp.key());
            rt.setRight(deletemin(rt.right()));
        }
    }
    return rt;
}

• printhelp

实现前中后序遍历结果打印，以下为中序遍历结果打印，调整语句顺序可改变打印顺序(*BST**中序遍历结果即从小到大排序)
时间开销：**Θ(**n)，需要遍历n个结点

private void printhelp(BSTNode<Key,E> rt) 
{
    if (rt == null) return;
    printhelp(rt.left());
    printVisit(rt.element());
    printhelp(rt.right());
}

5. 堆(heap)

堆是由数组实现的完全二叉树，同时必须是部分有序的(partially ordered)，并由此分为

• 最大堆max heap：任意结点的值都大于等于其子节点值

• 最小堆min heap：任意结点的值都小于等于其子节点值

  实现

  MaxHeap.java

  方法详解

• buildheap

给定任意长度n的原始数组，从下到上建立最大堆：
从下到上**建堆可以忽略最后一层的叶结点，可确定堆倒数第二层开始的下标，从右到左依次siftdown，下沉到合适位置，然后是倒数第三层…最终到顶层元素下沉，执行完毕可得到一个最大堆
时间开销：Θ(**n)

public void buildheap() 
{
    for (int i = n / 2 - 1; i >= 0; i--)
        siftdown(i);
}

• siftdown

下沉Heap[pos]到堆合适的位置
给定pos，**找出其两个子结点中较大的**;对比Heap[pos]和Heap[j]，大的作为父结点
时间开销：Θ(log**2**n)

/** Put element in its correct place */
private void siftdown(int pos)
{
    assert(pos >= 0) && (pos < n) : "Illegal heap position";
    while (!isLeaf(pos))
    {
        int j = leftchild(pos);
        if ((j < (n - 1)) && (Heap[j].compareTo(Heap[j + 1]) < 0))
            j++; // j is now index of child with greater value
        if (Heap[pos].compareTo(Heap[j]) >= 0)
            return;
        DSutil.swap(Heap, pos, j);
        pos = j; // Move down
    }
}

:::info 举例：建堆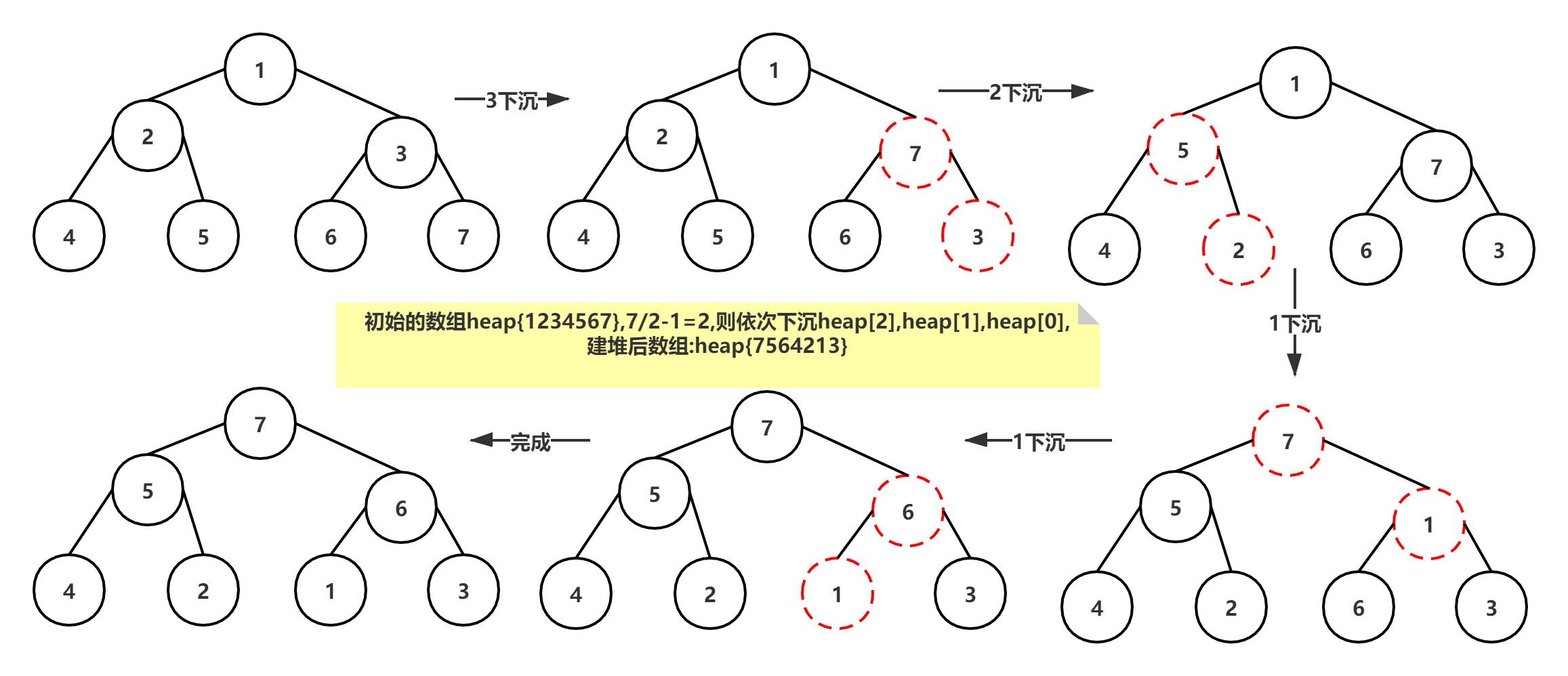
:::

• insert

插入新元素进堆
首先插入数组末端，然后与parent的值对比，上浮到合适位置
时间开销：Θ(log**2**n)

/** Insert val into heap */
public void insert(E val)
{
    assert n < size : "Heap is full";
    int curr = n++;
    Heap[curr] = val; // Start at end of heap
    // Now sift up until curr’s parent’s key > curr’s key
    while ((curr != 0) &&
           (Heap[curr].compareTo(Heap[parent(curr)]) > 0))
    {
        DSutil.swap(Heap, curr, parent(curr));
        curr = parent(curr);
    }
}

• removemax

移除堆顶(最大值)
实现时只需要交换堆顶/首元素和数组末尾元素，**同时—n，避免换到末尾的元素被访问，之后新堆顶重新下沉
时间开销：Θ(log2n)**

public E removemax()
{
    assert n > 0 : "Removing from empty heap";
    DSutil.swap(Heap, 0, --n); // Swap maximum with last value
    if (n != 0)                // Not on last element
        siftdown(0);           // Put new heap root val in correct place
    return Heap[n];
}
/** Remove and return element at specified position */

• remove

移除指定位置元素
实现时只需要交换Heap[pos]元素和数组末尾元素**，同时—n，避免换到末尾的元素被访问，**Heap[pos]处新元素先上浮，再下沉
时间开销：Θ(log**2**n)

public E remove(int pos)
{
    assert(pos >= 0) && (pos < n) : "Illegal heap position";
    if (pos == (n - 1))
        n--; // Last element, no work to be done
    else
    {
        DSutil.swap(Heap, pos, --n); // Swap with last value
        // If we just swapped in a big value, push it up
        while ((pos > 0) &&
               (Heap[pos].compareTo(Heap[parent(pos)]) > 0))
        {
            DSutil.swap(Heap, pos, parent(pos));
            pos = parent(pos);
        }
        if (n != 0)
            siftdown(pos); // If it is little, push down
    }
    return Heap[n];
}

:::info

• 逻辑上建成的偏序Heap和数组元素的排序无直接关系，最大堆不代表数组从大到小排列
• 对最大堆不断执行remove()后返回的所有元素依次排列为数组元素从大到小顺序 :::

6. 哈夫曼树(Huffman Tree)

给定文本，可以确定其中每个字母出现的频度，将频度作为权值，以这些”权值+字符”作为二叉树的叶子结点，构造一棵二叉树.每个叶子结点对应一个加权路径长度(WPL)：，若该树的加权路径长度达到最小**，**称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)，由定义知权值较大的结点离根较近，权值低的结点离根远. :::danger

建树过程：不断执行建立最小堆过程，每次结束后执行两次removemin()，取出权重最小两树，合并，然后重新insert()入堆，再次取出权重最小两树…直到堆中只剩一个元素，即为哈夫曼树
::: :::info 应用：为哈夫曼树的枝杈标记01后即可把字符转换为二进制编码，则高频字符编码短，低频字符编码长，这样可以节省文本存储空间
例题：已知文本中字符和频度：，建立哈夫曼树并求所有字符的哈夫曼编码与每个字符预期存储长度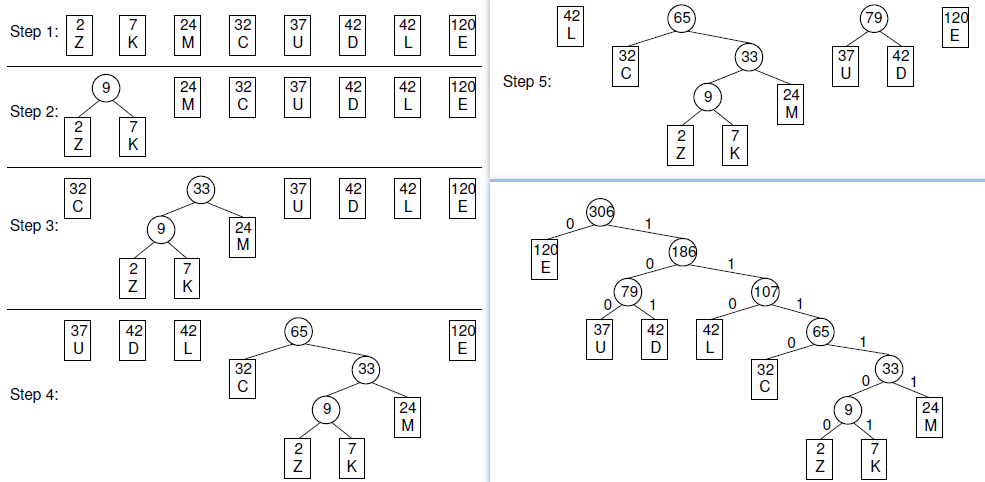


::: **