例4.1 后缀表达式的无二义性CFG构造
| 分析 | 通常后缀表达式如12+76-* - 优先级:1级->需2个非终态符号factor和exp - 结合性:左结合 |
|---|---|
| 解决 | - factor:num作为最小元素,且无()参与 |
factor->num
- exp:通常规则都是exp exp opt
exp->exp exp opt | factor,此时opt作为rule的最右侧已经满足左递归 |
| 结果 |
- exp->exp exp opt | factor
- factor -> num
化简: exp -> exp exp opt | num |
⭐例4.2 由num,id和二目运算符+,-,*,/构成表达式的CFG构造
| 分析 | 1级 左结合 * / 2级 左结合 + - |
|---|---|
| 解决 | - factor:num,id最小元素,可有()参与 |
factor->num | id | (exp)
- 1级:二目运算一般规则,取符号term
term->term term | term / term | factor
考虑左结合 **term->term factor | term / factor | factor
- 2级:二目运算一般规则,取符号exp
exp->exp + exp | exp - exp | term
考虑左结合 exp -> exp + term | exp -term | term |
| 结果 |
- exp -> exp + term | exp -term
| term
- term->term factor | term /
factor | factor
- factor->num | id | (exp)*
|
⭐例4.3 完整的LL(1)分析过程
有左递归,无左因子 | 消除左递归 | 整理文法 | | —- | —- | | L->SL’
L’->,SL’|ε | S->(L), S->a
L->SL’,
L’->,SL’, L’->ε |如下 | 消除左递归 | 整理文法 | | —- | —- | | first(S)={(,a}
first(L)={(,a}
first(L’)={, ,ε}
first((L))={(}
first(a)={a}
first(SL’)={(,a}
first(,SL’)={,} | ①由S->(L):
first())-ε∈follow(L) follow(L)={),$}
②由L->SL’
follow(L)∈follow(L’) first(L’)-ε∈follow(S)
follow(L’)={),$} follow(S)={, ,$}
③由L’->,SL’且first(L’)含有ε
follow(L’)∈follow(S)
first(L’)-ε∈follow(S) follow(S)={, , ) ,$}
最后
follow(S)={, , ) ,$} follow(L)={),$} **follow(L’)={),$}** |由a,b结果(提示:填表时始终对应拆分整理后的文法,一行一行扫描) | M[N,T] | ( | ) | , | a | $ | | —- | —- | —- | —- | —- | —- | | S | S->(L) | | | S->a | | | L | L->SL’ | | | L->SL’ | | | L’ | | L’->ε | L’->,SL’ | | L’->ε |
已知(()() | 步骤 | stack | input | action | | —- | —- | —- | —- | | 1 | S$ | (()()$ | S->(L) | | 2 | (L)$ | (()()$ | match | | 3 | L)$ | ()()$ | L->SL’ | | 4 | SL’)$ | ()()$ | S->(L) | | 5 | (L)L’)$ | ()()$ | match | | 6 | L)L’)$ | )()$ | ERROR |
例4.4 递归下降程序
构造
的递归下降分析程序
无左递归和左因子,求出first和follow集 | 文法 | first | follow | | —- | —- | —- | | A->(B)B, A->ε
B->A, B->ε | first(A)={(,ε}
first(B)={(,ε} first((B)B)={(} | follow(A)=
follow(B)={), $} |程序(递归下降程序无需写转换表,**需要first/follow集,但是没有对应case $) | A() | B() | match()** | | —- | —- | —- | | void A(){
switch(Token):
case ( :
match(();
B();
match());
B();
case ):
match(ε);
default: error;
} | void B(){
switch(Token):
case ( :
A();
case ):
match(ε);
default: error;
} | void match(expectedToken){
if(Token==expectedToken)
getToken();
else error;
} |
⭐例4.5 Bottom-Up算法综合
文法G:S->S(S)|ε
- 构造LR(0)项目集的DFA
- 构造SLR(I)分析表
- 给出句子(()()的SLR(1)分析过程
- 构造LR(1)项目集的DFA和LR(1)分析表
- 构造LALR(1)项目集的DFA和LALR(1)分析表
- 分析使用LR(1)和LALR(1)方法进行语法分析时,两者可能的不同
- 令S’->S,得到: ①S’->S ②S->S(S) ③S->ε
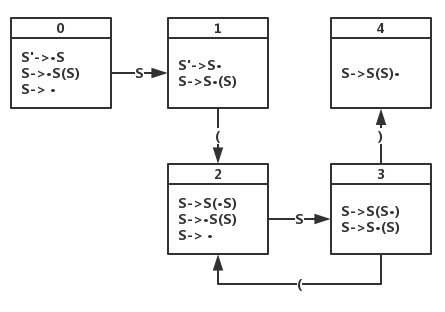
易错
- S->ε也要在DFA中表示为S->·,直接满足规约
- 状态2中S->S(·S),求其闭包将S的初始项目S->S(S),S->**ε继续加入**
- 分析表如下
follow(S’)={$},follow(S)={$,(,)}
| State | Action | Goto | ||
|---|---|---|---|---|
| ( | ) | $ | S | |
| 0 | r3 | r3 | r3 | 1 |
| 1 | s2 | acc | ||
| 2 | r3 | r3 | r3 | 3 |
| 3 | s2 | s4 | ||
| 4 | r2 | r2 | r2 |
易错
- 区分问的是LR(0)还是SLR(1)分析,二者DFA相同,分析表不同
- LR(0),不管任何符号都规约
- SLR(1)时,对A->γ,只有非终符号a∈Follow(A)时,才在表中对应位置填入r(A->γ)
- switch j表示转换到状态j,reduce k表示可规约文法k:A->B,序号意义不同
- acc填在扩展开始符号**S’可规约状态的$单元格中,此状态其他符号无需规约**
- 过程 | step | stack | input | action | 易错 | | :—-: | :—-: | :—-: | :—-: | :—-: | | 1 | $0 | (()()$ | r3 | 由③S->ε规约,得到S并入栈,Goto进入状态1,由于|ε|=0,出栈0个状态0个符号 | | 2 | $0S1 | (()()$ | s2 | 读入一个Token,switch到状态2 | | 3 | $0S1(2 | ()()$ | r3 | | | 4 | $0S1(2S3 | ()()$ | s2 | | | 5 | $0S1(2S3(2 | )()$ | r3 | | | 6 | $0S1(2S3(2S3 | )()$ | s4 | | | 7 | $0S1(2S3(2S3)4 | ()$ | r2 | 由②S->S(S)规约,得到S并入栈,Goto进入状态4,由于|S(S)|=0,出栈4个状态4个符号 | | 8 | $0S1(2S3 | ()$ | s2 | | | 9 | $0S1(2S3(2 | )$ | r3 | | | 10 | $0S1(2S3(2S3 | )$ | s4 | | | 11 | $0S1(2S3(2S3)4 | $ | r2 | | | 12 | $0S1(2S3 | $ | Error | 最终结果时Error/Acc不意味着stack一定要空 |
- LR(1)DFA如下
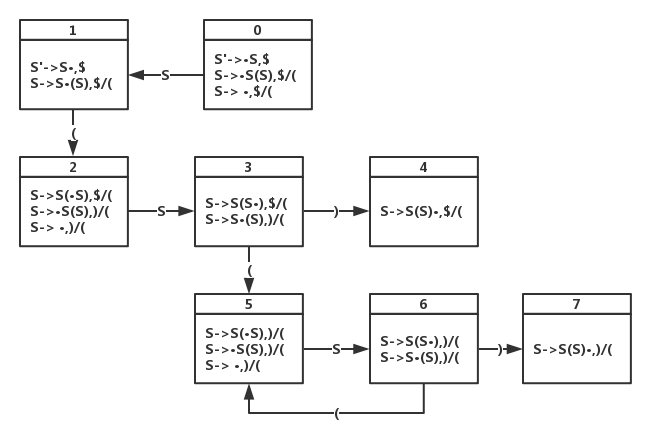
易错以状态0为例说明闭包的叠加:
1. 由文法直接得到 |
①S’->·S, $ ②S ->·S(S), $ ③S ->·, $ |
|---|---|
2. ②”·”后为非终S,继续加入产生式,根据向前看符号求法first(($)={(} |
④S ->·S(S), ( ⑤S ->·, ( |
3. 合并得到 |
①S’->·S, $ ②S ->·S(S), $/( ③S ->·, $/( |
分析表如下
| State | Action | Goto | ||
|---|---|---|---|---|
| ( | ) | $ | S | |
| 0 | r3 | r3 | 1 | |
| 1 | s2 | acc | ||
| 2 | r3 | r3 | 3 | |
| 3 | s5 | s4 | ||
| 4 | r2 | r2 | ||
| 5 | r3 | r3 | 6 | |
| 6 | s5 | s7 | ||
| 7 | r2 | r2 |
- LALR(1)的DFA如下:
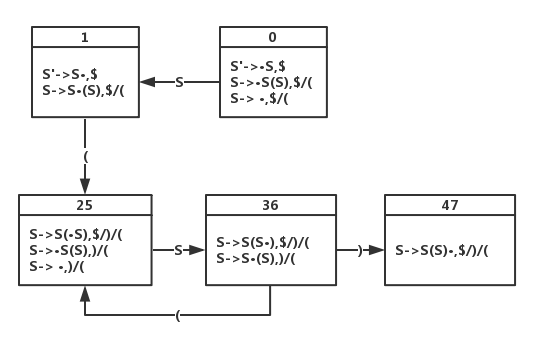
分析表如下
| State | Action | Goto | ||
|---|---|---|---|---|
| ( | ) | $ | S | |
| 0 | r3 | r3 | 1 | |
| 1 | s25 | acc | ||
| 25 | r3 | r3 | 36 | |
| 36 | s25 | s47 | ||
| 47 | r2 | r2 | r2 |
- 假设给定输入(() | (()()$ | r3 | | —-: | :—-: | | (()()$ | s2 | | ()()$ | r3 | | ()()$ | s2 | | )()$ | r3 | | )()$ | s4 | | ()$ | r2 |
| LR(1) | LALR(1) | ||||||
|---|---|---|---|---|---|---|---|
| step | stack | input | action | step | stack | input | action |
| 1 | $0 | (()$ | r3 | 1 | $0 | (()$ | r3 |
| 2 | $0S1 | (()$ | s2 | 2 | $0S1 | (()$ | s25 |
| 3 | $0S1(2 | ()$ | r3 | 3 | $0S1(25 | ()$ | r3 |
| 4 | $0S1(2S3 | ()$ | s5 | 4 | $0S1(25S36 | ()$ | s25 |
| 5 | $0S1(2S3(5 | )$ | r3 | 5 | $0S1(25S36(25 | )$ | r3 |
| 6 | $0S1(2S3(5S6 | )$ | s7 | 6 | $0S1(25S36(25S36 | )$ | s47 |
| 7 | $0S1(2S3(5S6)7 | $ | Error | 7 | $0S1(25S36(25S36)47 | $ | r2 |
| 8 | $0S1(25S36 | $ | Error |
LALR(1)比起LR(1)多进行了一步无意义的规约才发现错误
例4.6 Top-Down & Bottom-Up对比
- 自顶向下分析
- 构造语法树过程从根节点开始到叶子节点
- 从开始状态出发,根据给定产生式,推导出给定串
- 这种方法更易于手工构造出高效的语法分析器
- 自底向上分析
- 构造语法树过程从叶子节点开始到根节点
- 从给定的句子出发规约到文法开始符号
- 这种方法可处理更多种文法与翻译方案,应对可能产生二义性的文法,故分析软件多使用这种方法


