1. 二维随机变量及其分布函数
1.1 离散型
类似一维时,概率分布即为随机变量(X,Y)取特定值时的概率;二维分布函数可通过概率分布求和得到
联合概率分布/联合质量函数
联合分布函数
常见二维离散型分布
| 三项分布 | |
|---|---|
| 表示 | |
| 联合概率分布 | |
| 联合分布函数 | |
| 实际应用 | n重独立试验中,每次试验有 |
1.2 连续型
二维概率密度函数/联合密度函数
二维分布函数
:::info
如何理解二维分布函数:首先既然是二重积分,就大致是曲顶柱体体积,根据宋浩老师的说法,大致是一个”草帽”,F(x)就是草帽给定区间的体积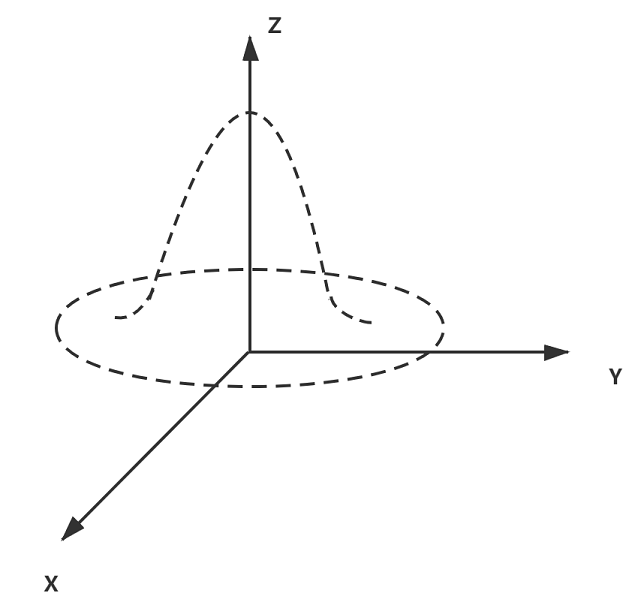
而联合密度函数f(x,y)就是上面这层曲顶对应的函数
:::
常见二维连续型分布**
| 均匀分布 | |
|---|---|
| 表示 | |
| 联合概率分布 | |
| 联合分布函数 | |
| 实际应用 | 描述(X,Y)等可能落入区域G中的随机点(对比一维均匀分布是落入区间[a,b]) |
2. 边缘分布及随机变量的独立性
二维变量(X,Y)中某一维分布函数相对于二维分布函数
被称为边缘分布函数
边缘分布函数
独立性
2.1 离散型
边缘概率分布/边缘质量函数
二维离散型随机变量边缘分布可通过联合概率分布求出
:::info
参考例题1: 二维离散,可以简要叙述边缘概率分布的意义:
- pi.:当考虑Y取得所有可能结果时,X分别等于xi时的概率
p.j:当考虑X取得所有可能结果时,y分别等于yj时的概率 ::: 独立性
2.2 连续型
边缘密度函数
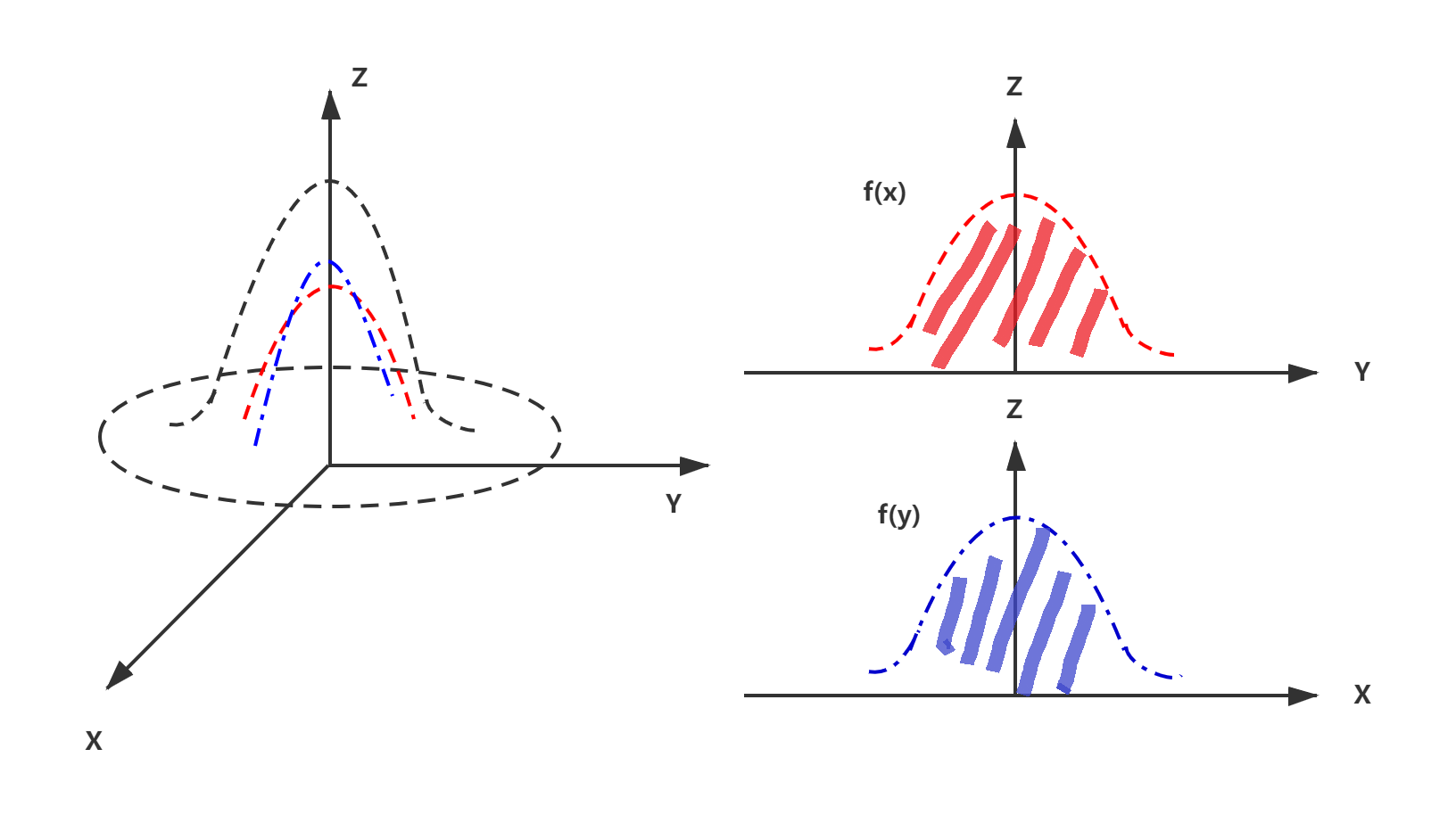
:::info 如何理解边缘密度函数:一重积分就是面积**:对边缘密度函数
来说就是给定某个x,此时曲顶对应一条曲线,把曲线投影到YOZ平面后的面积,因此对R上的y积分
- 对边缘密度函数
来说就是给定某个y,此时曲顶对应一条曲线,把曲线投影到XOZ平面后的面积,因此对R上的x积分
 :::
独立性
:::
独立性
3. 条件分布和条件密度
3.1 离散型
3.2 连续型
条件密度函数
条件分布函数
**
:::danger
上述结论的证明有点技巧,首先,对于连续随机变量,某点的概率取值为0,因此分母直接为0,有点反直觉,其证明如下(不清楚可看宋老师视频24min处):
此时使用积分中值定理,在区间[y,y+ε]中可找到ξ使得
则分母变成常数,分子同样使用中值定理得到
综上
:::
:::info 在做题中,通常有两种问法
- 问
此时为条件分布知识,使用
- 问
此时并非条件分布:
分子为一般二维分布函数
分母为边缘分布函数
:::
4. 二维随机变量函数的分布
4.1 离散型
4.2 连续型
求的一般方法:
**

