化二进制

  • 整数:除2取余(自下而上,直到商为0)
  • 小数:乘2取整(自上到下,直到小数部分为0)

C位运算

  • 反码ONES’ COMPLEMENT ( ~ ),
  • 位移SHIFT ( << and >> )
    • 左移时丢弃高位,低位补0
    • 右移有符号数,算术右移,丢弃低位,高位补符号位
    • 右移无符号数,逻辑右移,丢弃低位,高位补0
  • 与AND ( & ),
  • 或OR ( | ),
  • 异或EXCLUSIVE OR ( ^ ):同假异真
  • 注意!为逻辑非,C中对除0以为任何数使用!都得到0


CSAPP datalab⭐

参考链接: 实验二 datalab-handout
实现按位&,|,^操作

  1. /* 
  2.  * bitAnd - x&y using only ~ and | 
  3.  *   Example: bitAnd(6, 5) = 4
  4.  *   Legal ops: ~ |
  5.  */
  6. int bitAnd(int x, int y) {
  7.   // ~(~A∪~B)=A∩B
  8.   return ~(~x|~y);
  9. }
  11. /* 
  12.  * bitOr - x|y using only ~ and & 
  13.  *   Example: bitOr(6, 5) = 7
  14.  *   Legal ops: ~ &
  15.  */
  16. int bitOr(int x, int y) {
  17.   // ~(~A∩~B)=A∪B
  18.   return ~(~x&~y);
  20. }
  22. /* 
  23.  * bitXor - x^y using only ~ and & 
  24.  *   Example: bitXor(4, 5) = 1
  25.  *   Legal ops: ~ &
  26.  */
  27. int bitXor(int x, int y) {
  28.   return (x & ~y) | (~x & y);
  29. }

求-1
1表示为32bits二进制000…001,数据位补码111…111,加符号位后转换为16进制,0xffffffff

  1. /* 
  2.  * minusOne - return a value of -1 
  3.  *   Legal ops: ! ~ & ^ | + << >>
  4.  *   Max ops: 2
  5.  */
  6. int minusOne(void) {
  7.   return ~0;
  8. }

求2s补码下最大整数
正常int的最大整数为0111…..1111,对齐取反1000…0000,那么通过0000…0001左移即可

  1. /* 
  2.  * TMax - return maximum two's complement integer 
  3.  *   Legal ops: ! ~ & ^ | + << >>
  4.  *   Max ops: 4
  5.  */
  6. int tmax(void) {
  7.   return ~(1 << 31);
  8. }

字节提取

  1. /* 
  2.  * getByte - Extract byte n from word x
  3.  *   Bytes numbered from 0 (LSB) to 3 (MSB)
  4.  *   Examples: getByte(0x12345678,1) = 0x56
  5.  *   Legal ops: ! ~ & ^ | + << >>
  6.  */
  7. int getByte(int x, int n) {
  8.   return (x >> (n << 3)) & 0x000000ff;
  9. }

求相反数
即求2s补码

  1. /* 
  2.  * negate - return -x 
  3.  *   Example: negate(1) = -1.
  4.  *   Legal ops: ! ~ & ^ | + << >>
  5.  */
  6. int negate(int x) {
  7.   return (~x)+1;
  8. }

判断相等/等于0

  1. /* 
  2.  * isEqual - return 1 if x == y, and 0 otherwise 
  3.  *   Examples: isEqual(5,5) = 1, isEqual(4,5) = 0
  4.  *   Legal ops: ! ~ & ^ | + << >>
  5.  */
  6. int isEqual(int x, int y) {
  7.   return !(x^y);
  8. }
  10. /*
  11.  * isZero - returns 1 if x == 0, and 0 otherwise 
  12.  *   Examples: isZero(5) = 0, isZero(0) = 1
  13.  *   Legal ops: ! ~ & ^ | + << >>
  14.  */
  15. int isZero(int x) {
  16.   return ! (0^x);
  17. }

判断为正数,判断非负数

  • 为正数:符号位为0,且非0
  • 非负数:符号位为0,或为0 ```c /*
    • isPositive - return 1 if x > 0, return 0 otherwise
    • Example: isPositive(-1) = 0.
    • Legal ops: ! ~ & ^ | + << >> */ int isPositive(int x) { return !((x >> 31) | (!x)); }

/ isNonNegative - return 1 if x >= 0, return 0 otherwise

  • Example: isNonNegative(-1) = 0. isNonNegative(0) = 1.
  • Legal ops: ! ~ & ^ | + << >> */ int isNonNegative(int x) { return !(x >> 31); }
  2. ---
  4. <a name="2Yy0J"></a>
  5. ### 浮点数
  6. IEEE Standard 754浮点数格式<br />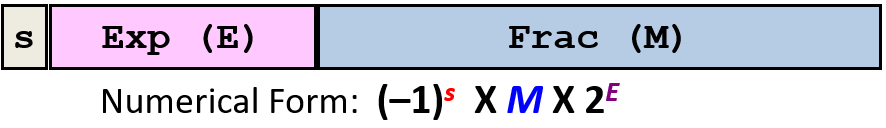![1.png](https://cdn.nlark.com/yuque/0/2019/png/670787/1576761981056-ba0ed1b7-24c7-47bf-b64a-4965851d9524.png#crop=0&crop=0&crop=1&crop=1&height=69&id=cv38h&name=1.png&originHeight=128&originWidth=886&originalType=binary&ratio=1&rotation=0&showTitle=false&size=8713&status=done&style=none&title=&width=479)
  8. | **结构** | 符号位sign: **正0负1**<br />阶码 Exponent: 决定小数点的位置: **Exp(阶码) = E (真值)+Bias(偏移量)**<br />分数 Fraction:指示[1 , 2]之间的数: **Frac = M - 1** |
  9. | --- | --- |
  10. | **规格** | 单精度: 8 Exp, 23 Frac, 1 sign = 32<br />双精度: 11 Exp, 52 Frac, 1 sign =64 |
  11. | **举例** | **float F  = 15213.0化为单精度浮点数求Exp: **<br />15213 = 11101101101101 = 1.1101101101101 X 213<br />得到E=13,偏移量27-1=127,13+127=140化为二进制10001100作为Exp<br />**求Frac:**<br />M = 1.1101101101101,Frac = 11011011011010000000000(补齐23bits)<br />最终:0,10001100, 11011011011010000000000<br />逆运算根据IEEE表达求出原数**(-1)****S**** * 2**** exp - 127 ***** (1 + frac * 2****-23****)**<br />![](https://cdn.nlark.com/yuque/__latex/1831aae0d5b46707c7ab8258907b86ff.svg#card=math&code=%28-1%29%5E%7B0%7D%2A2%5E%7B13%7D%2A%281%2B%282%5E%7B22%7D%2B2%5E%7B21%7D%2B2%5E%7B22%7D%2B2%5E%7B19%7D%2B2%5E%7B18%7D%2B2%5E%7B16%7D%2B2%5E%7B15%7D%2B2%5E%7B13%7D%2B2%5E%7B12%7D%2B2%5E%7B10%7D%29%2A2%5E%7B-23%7D%29%3D15213&height=23&id=J0Y5G) |
  14. ---
  16. <a name="qQY9N"></a>
  17. ### 浮点数加法
  18. 浮点数加法需要经过"对阶",容易丢失精度:十进制下10.375 + 6.34375 = **16.71875**<br />![](https://cdn.nlark.com/yuque/__latex/eb2a88bd0039a31a7c9c80b86344c04e.svg#card=math&code=%5C%5C%5Cfrac%7B%5Cbegin%7Balign%7D%0A1.0100110%C3%972%5E3%5C%5C%0A%2B%5Cquad0.1100110%C3%972%5E3%0A%5Cend%7Balign%7D%7D%7B10.0001100%C3%972%5E3%7D%5CLongrightarrow16.75%5Cquad%20precision%5C%20loss&height=69&id=hzvXw)
  20. ---
  22. <a name="9F1JN"></a>
  23. ### 选择题知识点
  25. 1. 在4byte为一个word的计算机中,下列哪一个表达式测试指针ptr是否包含某个word的地址
  26. ```c
  27. (ptr & 3) == 0
  28. (ptr | 3) == 0
  29. (ptr % 4) == 0

选Ⅰ和Ⅲ(指针不可以做%或&运算,需要强转)

  • Ⅰ计算机4bytes为一个word,见指针,每个字节有一个地址,所以每个word的地址都以4对齐,下图为VS调试时内存窗口4字节显示结果,明显看到16进制表示时最后字节以0,4,8,c变化,对应0000 0000, 0000 0100, 0000 1000, 0000 1100

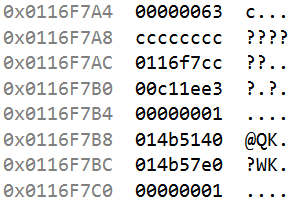
image.png
最后2bit始终为00与0011按位与的结果永远是0

  • Ⅲ把最后字节化为int类型:0,4,8,12对4取余恒为0

  1. 关于溢出

    • C程序对整型加法中的溢出不会产生提醒,会得到错误结果;
    • 对浮点数溢出,即阶码部分超过其能表示的最大值时报错#INF:infinity

  2. 以下结果是false的是:0x00 ^ 0x00

    1. #include <stdio.h>
    2. #include <stdbool.h>
    3. void main()
    4. {
    5.  bool a = !(0);
    6.  bool b = ~(0xFF);
    7.  bool c = ~(0x00);
    8.  bool d = 0x00 ^ 0x00;
    9. }

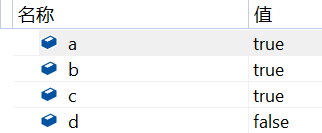    | image.png | 在bd中犹豫,实际上C语言没有bool,所有bool都根据int截取,b按位取反:0x000000ff->0xffffff00,结果为负数,求二进制下31bits数据位原码,取反加一(100)2即-256,在C中只要非0的数都为true,因此b是true | | —- | —- |