1. 好的关系设计
1.1 函数依赖
(functional dependency)
前提**:**关系模式的表示法
- 使用希腊字母表示属性集(α,β…)
- 使用大小写组合指示关系模式(r(R)),此时r表示关系r,R表示属性集合,当关系名称不重要时,只用R
- 如employee(id, name),简化(id, name)
- 当属性集是超码(一个或多个属性的集合,课区分唯一实体),用K表示,K是r(R)的超码
- 有时关系或关系的实例可仅用小写字母表示,如r
场景:**分析关系模式**
给定关系inst_dept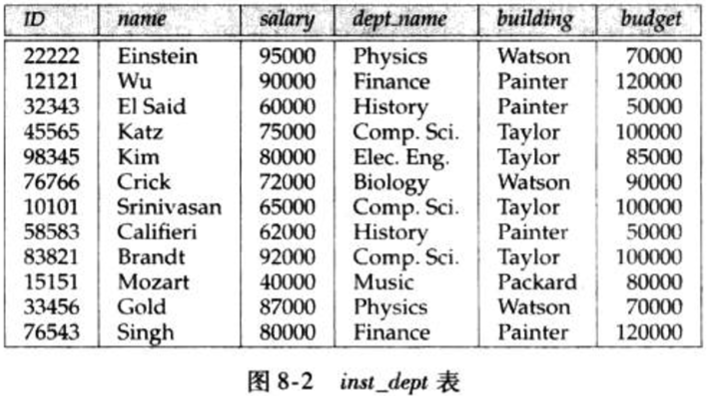
- 如果此时要求:每个系对应一个预算
- 需要:设计者在dept_name非当前模式主码情况下也能规定”一个dept_name对应一个budget”
- 等价于:如果有模式(dept_name, budget),则dept_name可以做主码,表示如下,即为函数依赖
- 通过该依赖可以发现inst_dept关系产生了大量重复记录,需要拆分为instructor, departmet
| 函数依赖 | 给定r(R)的实例,当实例满足函数依赖α->β的条件:
实例中所有元组对t1和t2,若t1[α]=t2[α],则t1[β]=t2[β] | | :—-: | —- | | 作用 | 函数依赖帮助设计者发现模式是否冗余,需要拆分 | | 个人理解 | 函数依赖是关系模式中属性或属性集间需要遵循的约束,由函数的角度可以视为不同属性间的映射f:α->β,函数具有单值的性质,函数依赖也类似,不允许出现在R中属性集α可以对应多个β |
1.2 关系模式的分解
| 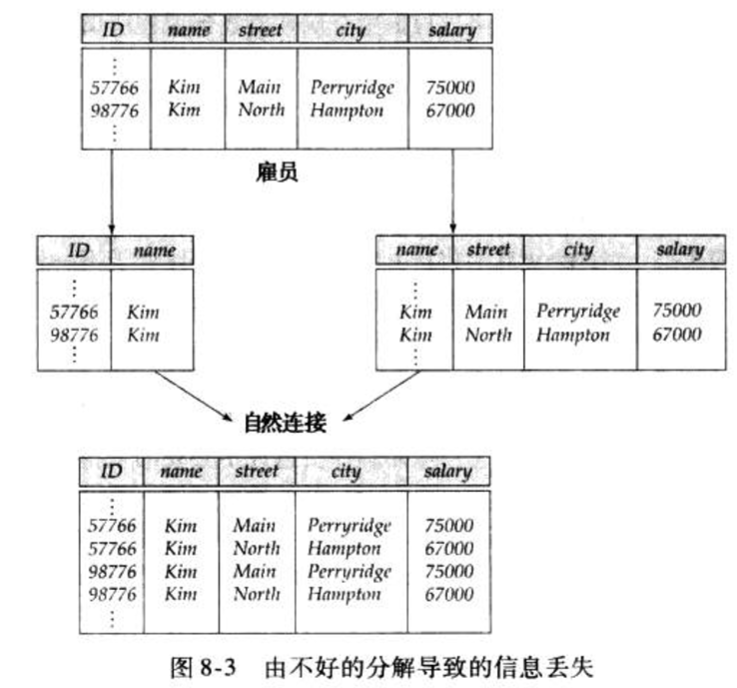 |
|
- 给定关系模式:
employee(ID,
name, street, city, salary)
按左图分解,右侧关系中可以知道某个(street,
city, salary)下有个Kim,对于某大学中两个Kim,自然连接后产生4个结果,无法确定哪个是有意义的,称为有损分解
- 分解:
- 有损分解: lossy decomposition
- 无损分解: lossless decomposition
|
| —- | —- |
2. 原子域和第一范式
(atomic domain & first normal form)
参考链接: 范式理解与判断
概念引入:设计者根据函数依赖和其他数据依赖定义范式,再通过设计满足适当范式的模式来避免关系模式的冗余
函数依赖/数据依赖——>设计范式——>避免冗余
| 原子域 | 关系模式中,域指属性可取值的集合,而原子域的元素都是不可分的单元 |
|---|---|
| 第一范式 | 关系模式R的所有属性的域都是原子的 |
| 非原子域 ** |
非第一范式** | employee(id, name, children)中children是多值属性,即children取值可分,则关系具有非原子域,模式不属于第一范式 |
3. 使用函数依赖分解
3.1 码和函数依赖
| 函数依赖定义超码 | 如果函数依赖K->R在r(R)上成立,当K是r(R)超码: 对在r(R)的每个合法实例,实例中的每个元组对t1,t2,若t1[K]=t2[K]总有t1[R]=t2R,则K是一个超码 |
|---|---|
| 函数依赖表示无法用超码表示的约束 | 对前文inst_dept(ID, name, salary, dept_name, building, budget)要求dept_name->budget成立,即 |
(ID, dept_name)构成inst_dept的一个超码,记为
ID,
dept_name->name, salary, building, budget |
3.2 函数依赖的使用
- 判定关系的实例是否满足给定函数依赖集F(被多个函数依赖约束)
- 说明合法关系集上的约束
举例
| 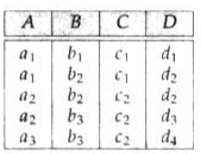 | 左侧关系r下:
| 左侧关系r下:
✔满足函数依赖A->C
❌不满足函数依赖C->A | 平凡(trivial)依赖:在所有关系都满足的依赖
如:A->A,AB->A
若β⊆α,则形如α->β的都是平凡依赖 | 依赖闭包(closure):集合闭包F是根据F可推导出的所有函数依赖
如:给定r(A,B,C)若F:A->B,B->C在r上成立,则A->C一定成立,此时A->B,B->C,A->C共同构成F |
| —- | —- | —- | —- |
3.3 BC范式
(BCNF-Boyce-Codd Normal Form)
| BCNF | 具有函数依赖集F的关系模式R属于BCNF的条件:对F+中所有形如α->β的函数依赖(α⊆R且β⊆R),下面至少一项成立
- α->β是平凡依赖(β⊆α)
- α是模式R的一个超码
一个数据库设计属于BCNF的条件即设计的关系模式集中每个模式都属于BCNF |
| :—-: | —- |
| 举例 | inst_dept非BCNF,设计时要求”系-办公楼和预算”一一对应
inst_dept(ID, name, salary, dept_name, building, budget)的F中有dept_name->budget, building,但dept_name本身非超码,因此模式中有冗余,需要拆分为instructor, department
这两个关系是BCNF:因为设计要求的F中α->β形依赖,除去平凡依赖,其余α都是超码:
dept_name->budget, building |
| 非BCNF分解⭐ | 设R为非BCNF的一个模式,即存在至少一个非平凡α->β,使用以下两种模式取代R:
- (α∪β),eg:(dept_name, budget, building)
- (R-(β-α)),eg:(ID, name, dept_name, salary)
分解非BCNF后,产生的子模式可能依旧有一个或多个非BCNF,需要继续分解,最终结果为BCNF模式集合 |
4. 第三范式
4.1 BCNF的局限
给定以下联系集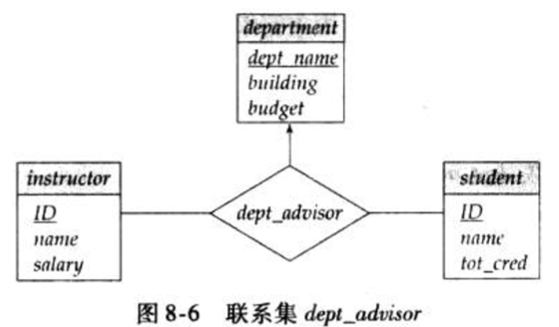
| 要求 | - 一个教师只能在一个系担任教师 - 给定一个系,一个学生最多一个导师 |
|---|---|
| 依赖 | 对应dept_advisor(s_id, i_id, dept_name)一定有以下函数依赖 - 依赖一: i_id->dept_name - 依赖二: dept_name, s_id->i_id |
| 问题 | 依赖一,i_id非超码(一个导师在某个系内可带多个学生) 依赖二,成立 |
| 分解 | (i_id, dept_name)和(s_id, i_id) 根据依赖一分解后均为BCNF(任何二属性关系模式都是BCNF),但无法保持依赖二 |
| 不足 | 有时的设计使得保持依赖(dependency |
preserving)很困难,需要一种比BCNF约束要弱的范式,设计的同时保持依赖—第三范式 |
4.2 3NF
具有依赖集F的关系模式R属于3NF的条件,对F+中所有形如α->β的函数依赖(α⊆R且β⊆R),下面至少一项成立
- α->β是平凡依赖
- α是R的一个超码
- β-α中每个属性A都包含于R的一个候选码(最小超码)中(β-α中每个属性A可以包含于不同候选码,无需同时在一个中满足)
根据定义,非3NF一定非BCNF
**举例⭐
| 依赖一: i_id->dept_name | α=i_id,
β=dept_name
dept_name-i_id
= dept_name | 在无法满足BCNF情况下:
为了保持依赖二成立,又(dept_name,s_id)是一个候选码,包含dept_name,因此该模式为3NF |
| —- | —- | —- |
| 依赖二: dept_name, s_id->i_id | | |
5. 函数依赖理论
5.1 函数依赖集的闭包F+
| 逻辑蕴含 | 对r(R),给定依赖集F,当r(R)每一个满足F的实例也满足f,则f被r上依赖集F逻辑蕴含(logically imply) 离散数学中的蕴含关系p->q,只有p真q假时为假.依赖集F->f即当所有实例满足F,则一定满足f |
|
|---|---|---|
| 依赖集闭包 | 根据逻辑蕴含定义,F+就是被F逻辑蕴含的所有函数依赖的集合 | |
| armstrong公理系统 | 使用下列规则可寻找逻辑蕴涵的函数依赖: - 自反律(reflexivity rule):若β⊆α,则α->β成立 - 增补律(augmentation |
rule):若α->β成立且γ也为属性集,则γα->γβ成立<br />- 传递律(transitivityrule):若α->β且β->γ,则α->γ<br />- 合并律(union rule): α->β和α->γ成立,作为α->βγ<br />- 分解律(decomposition): 若α->βγ成立,则α->β和α->γ成立<br />- 伪传递律(pseudotransitivityrule):若α->β和γβ->ξ成立,则αγ->ξ成立<br /> | |
| 滚雪球算法 |  | 算法可结束:
| 算法可结束:
对n元素的集合,有2n个子集,对形如α->β的依赖,左右都为子集,则共有2n*2n=22n个依赖,除了最后一次,每次迭代repeat中至少新加了一个f,则算法一定可以结束
(滚雪球求,F+很少用,计算量巨大) |
5.2 属性集闭包⭐
| 函数确定 | 若α->B(非β,只是单个属性B),则称属性B被α函数确定(functionally determine) | |
|---|---|---|
| 属性集闭包⭐ | 将给定依赖集F下被α函数确定的所有属性的集合称为F下α的闭包α+ | |
| 判断超码 | 若要判断α是否为超码 - 计算F+,找出所有形如α->β的f,合并右半部分—>开销大 - 属性闭包算法 |
|
| 属性闭包算法 |  |
|
| 例题⭐ | 对r(A,B,C,G,H,I),F如下 求(AG)+ |
result=AG A->B中:A⊆result,result=result∪B =AGB A->C中:A⊆result,result=ABCG 同理对CG->H,CG->I,B->H |
最终result=ABCGHI即(AG)+,则(AG)是超码
|
| 算法作用⭐ | 判断α是否为超码 | α+=R时,R中每个属性都可由α确定,α为超码 |
| | 通过检查是否β⊆α+,检查α->β是否成立 | 当β⊆α+,说明α可以在给定F下确定β |
| | 计算F+:
对任意γ⊆R,找出F可确定的所有属性,组成闭包γ+
再对任意S⊆γ+,输出函数依赖γ->S,因为γ->S是F约束下确定的依赖,则也一定是F+中一个函数依赖,同理γ->γ+也是F+中一个依赖
(作为5.6 保持依赖算法中算法二依据) | 使用上面例题:
(AG)+=ABCGHI,则有:
AG->A,AG->B,AG->C,AG->G,AG->H,AG->I,
AG->ABCGHI都是F+中的依赖 |
5.3 正则覆盖
(canonical cover)
| 检测 | F下的关系模式r(R),必须保证用户更新数据库后依旧满足F,这就需要检测,当检测不满足F时,回滚该操作
简化方法:通过测试与给定F具有相同依赖闭包的简化集的方式减少检测开销
原理:简化集和原集闭包相同,满足简化集的数据库一定也满足原集 |
| :—-: | —- |
| 无关属性⭐
PDF__221 | 去除函数依赖集中某个依赖的一个属性,不改变依赖集的闭包,则(此依赖中的)该属性无关(extraneous):
考虑F和F中的函数依赖f:α->β
- 如果A∈α且F逻辑蕴涵(F-{α->β})∪{(α-A)->β},则属性A在α中无关
α->β,判断A在α中无关,要求依赖闭包在剔除A后不变,A的存在为了推出β:
只需说明F->{(F-f)∪((α-A)->β)},由公理,只需证F->{(α-A)->β},即β的推出和A本身无关:
为此,计算F+,当(α-A)->β)⊆F+,则A在α中无关
- 如果A∈β且依赖集(F-{α->β})∪{(α->(β-A)}逻辑蕴涵F,则属性A在β中无关
α->β,判断A在β中无关,要求依赖闭包在剔除A后不变,A的存在为了维持β,进而维持F:
只需说明{(α->(β-A))∪(F-f)}->F,即F只用(α->(β-A))和(F-f)就能得到,与β中A无关:
为此,计算F下的闭包((α->(β-A))∪(F-f))+,当F⊆((α->(β-A))∪(F-f))+,则A在β中无关
- 注意,上述两个蕴含关系在左右相反后恒成立
|
| 正则覆盖⭐ | Fc是一个依赖集,使得F逻辑蕴涵Fc中所有依赖,并且Fc逻辑蕴含F中所有依赖.此外Fc必须有如下性质:
- Fc中任何函数依赖都不含无关属性
- Fc中函数依赖的左半部都是唯一的
F<->Fc,对应离散数学中的”当且仅当(充要条件)”,因此检验Fc和检验F的真值表应该一模一样,Fc即为”简化集” |
| 算法⭐ | 
当遇到Fc=A->C,两侧都只有一个属性的属性集时,如果有一个无关属性,则这样空属性的函数依赖也要剔除 |
| 非唯一性⭐ |
Fc初始化为F后,在Fc中选取不同的依赖f进行无关性检验并删去后,最终的到的正则覆盖结果不唯一
|
例题
对下列F求正则覆盖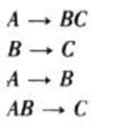
Fc初始化为F
合并:
Fc: A->BC,B->C,AB->C
检验Fc的无关属性:
| A在AB->C中无关 | 只需说明(B->C}能被Fc进一步推出:
B->C就在Fc中,则A无关
Fc变为A->BC,B->C |
| —- | —- |
| C在A->BC中无关 | 只需说明A->B可在Fc-f下进一步推出Fc:
A->B和B->C可推出A->C,A->C和A->B可推出A->BC,则可推出Fc中所有依赖,C无关,Fc变为A->B,B->C |
所以正则覆盖为:A->B, B->C
5.4 二元无损分解
(lossless decomposition)
| 无损分解 | F是r(R)上的函数依赖集,令R1,R2为R的分解,若用r1(R2)和r2(R2)替代r(R)时没有信息损失,则称分解是无损分解. |
|
|---|---|---|
| 关系代数角度⭐ | select * from`(select R1 from r) |
as r1<br />natural join<br />(select
R2 from r) as r2` | 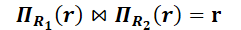
将r投影到R1和R2上,对投影结果自然连接,若结果与r相同,则为无损连接,否则有损连接,如1.2 关系模式的分解中的例子,最后自然连接的结果为四个元组 |
| 函数依赖角度⭐ |
- R1∩R2->R1
- R1∩R2->R2
以上依赖中至少一个在F+中,R1,R2就为无损分解,即R1∩R2是R1或R2的超码:采用属性闭包算法,当(R1∩R2)+=R1或R2即为无损分解
| |
| 充分条件 | 满足二元分解测试->证明是无损连接
但只有所有的约束都是函数依赖时才能说明:
满足无损连接->二元分解测试成立 | |
5.5 保持依赖
| 保持依赖 | 上文BCNF局限中的分解问题遇到了无法保持依赖的问题:
当有R的F中有f1,f2成立,f1满足BCNF要求,f2不满足,从而分解,再次判定f2满足,但没有Ri满足出现f1所有属性
实际上,对于Ri,F中所有α->β依旧保持,下面是证明 |
| :—-: | —- |
| 限定:Fi | 令F为模式R上的依赖集,R1,R2…Rn为R的分解.F在Ri上的限定是F+中所有只包含Ri中属性的函数依赖集合Fi.由于一个限定中的所有函数依赖只涉及一个R中的属性,因此判定这种依赖是否满足可以只检查一个关系Ri.
Ri是全体属性R中的部分属性,Fi是F中只与这些属性有关的函数依赖 |
| 限定的并集:F’ | 根据限定的定义,F1,F2…Fn的集合就成为可以高效检查的依赖集.令F’=F1∪F2∪…∪Fn,F’是R上一个依赖集,通常F’≠F,但可能有F’+=F+
如果后者成立,则F中所有依赖都被F’逻辑蕴含,只要证明满足F’,就满足了F,称具有F’+=F+的分解为保持依赖的分解(dependency-preserving
decomposition)
当**F’+=F+成立,F+⊆F’+,又F⊆F+,则F⊆F’+,**根据属性闭包算法,F’->F,**如果所有依赖满足F’即满足F** |
5.6 保持依赖验证算法
| 算法 | 思想 |
|---|---|
输入:D(R1,R2…Rn)和R的依赖集F |
求F+➡求出所有限定Fi➡并取所有限定,得F’➡计算F’+➡比较F’+和F+ 👹弊端: 要计算F+,开销大 |
| 算法的根本目标:证明模式R中所有F下的α->β在分解R1,R2…Rn中依旧保持 | |
| 算法依据:5.5 限定的并集F’,只要保证α->β在F’下保持 | |
| 算法实现:计算F’下α的闭包,当β⊆α+时,根据5.2 属性闭包算法作用,α->β成立,即α->β在F’中保持,当且仅当每一个α->β都保持,该分解是依赖保持的 | |
对F中每个α->β 此时属性闭包都是F下的: - 若result含有β所有属性,则α->β保持 - 当且仅当F中所有α->β都保持时,所有分解Ri都保持依赖 |
算法的根本目标:同上 |
| 算法依据:见5.2 属性闭包算法作用中作用三,对每个γ⊆Ri: - γ作为R中属性:γ->γ+是F+中函数依赖 - γ作为Ri中属性:γ->Ri是Fi/F’中函数依赖 - γ->(γ+∩Ri)成为F+在Ri上限定Fi/F’中的依赖 |
F+在Ri上限定Fi中的依赖:指在Ri中依旧保持的F+中依赖,而(γ+∩Ri)是该依赖可确定的属性集 |
| | 算法实现:result初始为α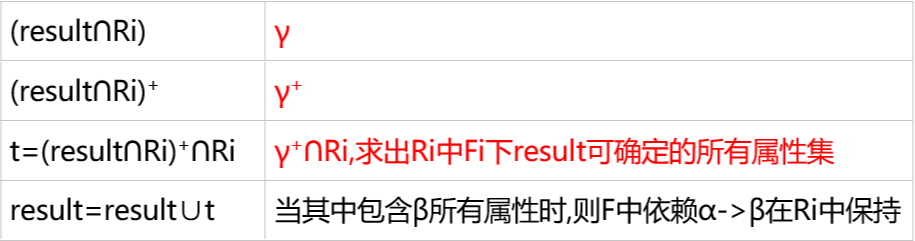
while每次对一个Ri操作,验证F+中依赖在Fi中保持,当result不变,相当于验证每个依赖在F’下保持 |
5.7 候选码求法—LRN法
| FD属性分类 | L类 | 仅在FD左边出现的属性 |
|---|---|---|
| R类 | 仅在FD右边出现的属性 | |
| N类 | 在FD两边均未出现的属性 | |
| LR类 | 在FD两边均出现的属性 | |
| 定理 & 推论⭐ |
定理1 | 对给定R和F,当x∈R是L类属性,则x一定是候选码关键字成员 |
| 推论1 | 对给定R和F,当x∈R是L类属性,且x+包含了R的所有属性,则x是唯一候选码 | |
| 定理2 | 对给定R和F,当x∈R是R类属性,则x一定非候选码关键字成员 | |
| 定理3 | 对给定R和F,当x∈R是N类属性,则x一定是候选码关键字成员 | |
| 推论2 | 对给定R和F,当α∈R是N和L组成的属性集合,且α+包含R所有元素,则α是唯一候选码 | |
| 步骤⭐ | 1. 使用LRN法求出L,R,N,LR类属性集合 1. 求L中元素闭包,当L中属性(集)闭包等于R,则为唯一候选码[推论1],如果非R,则依次并入LR中元素,直到闭包满足R |
6. 分解算法
6.1 BCNF判定
| 一般判定 | 参照5.2 属性闭包算法,即判断α+是否等于R,可以证明: 只要F中的依赖都满足BCNF,F+中的也都满足 |
|---|---|
| 分解后判定⭐ | 当有R的F中有依赖不满足BCNF,从而分解,再次判定,但当前没有依赖包含Ri中所有属性,无法准确判断 例子:分解后  F中没有依赖能够判定R2是否满足BCNF,不能简单认为这种情况下就默认满足,伪传递律可得到AC->D,R2不满足,有时需要一个来自F+而不在F中的依赖才能额外判断这种情况 |
| 改进判定⭐ |  实战中非常重要的判定 |
6.2 BCNF分解算法
即第三部分3.3 BC范式:非BCNF的分解原理:R-β+α=>Ri-β
α->Ri不属于F+,这项要求保证了不会产生冗余的依赖,非常重要
结果
该算法产生无损的BCNF分解:
- 使用(Ri-β)和(α,β)取代模式Ri后,依赖α->β成立,且(Ri-β)∩(α,β)=α,参考无损分解的函数依赖角度,相当于(Ri-β)∩(α,β)->(α,β)属于F+,是无损分解
- 若没有要求α∩β=Ø,那α∩β中的属性不会出现在(Ri-β)中,那α->β不再成立
6.3 3NF分解算法
| | 3NF算法中有两点注意:
| 3NF算法中有两点注意:
- 若所有Rj都不含R的候选码时,就需要额外创建一个关系模式,其中属性就是R的任意候选码
- 模式可能产生冗余:如R1(A,B)R2(A,B,C)这是就可以删除R1,令R2=R1
| :—-: | —- |<br /><br />算法证明:<br />_PDFP227_<br /> |
例题
以4.1图中dept_advisor(s_id, i_id, dept_name)为例, 要求满足的两个依赖为:
- i_ID->dept_names_ID
- dept_name->i_ID
而且恰好为Fc,则R1=(i_ID, dept_name),R2=(s_ID, dept_name, i_ID),又因为(s_ID, dept_name)就是候选码,无需创建新模式,但R1产生冗余,删去,最终产生保持依赖且无损的3NF,R(s_ID, dept_name, i_ID)
- 3NF**算法拓展⭐**
3NF算法的结果可能属于BCNF,因此进行BCNF分解可以:
先使用3NF算法,对结果中不满足BCNF的进行分解,如果结果没有保持依赖,则只能恢复到3NF,否则就是BCNF
6.4 3NF对比BCNF
| 3NF | BCNF | |
|---|---|---|
| 优点 | 可以在无损且保持依赖的情况下得到设计 |
|
| 没有冗余 | ||
| 缺点 | 可能需要null占位保持某些联系,或者可能有冗余 | 无法保持某些函数依赖 |
| sql设计 | 大多数数据库系统在检查非主码约束的函数依赖很困难,因此3NF的妥协导致了设计时的困难 | 对于无法保持的依赖,使用物化视图计算被拆散的依赖,投影为αβ,利用unique(α)或primary |
key(α)可以在物化视图上检查这些依赖 | | 实际 | 在无法得到保持依赖的BCNF分解时,优先考虑使用物化视图的BCNF,而非3NF | |
7. 多值依赖和其余范式
| 教材 | 参考PDF228开始内容 |
|---|---|
| 知乎 | 关于函数依赖和范式的知乎回答: 如何解释关系数据库的第一第二第三范式? - 刘慰的回答 - 知乎 |
8. 数据库设计过程
| 得到r(R)的三种方式 | - 直接由ER图转换 - r(R)开始包含所有属性,然后在规范化时不断分解 - 即席设计,类似预算要求,直接分析得到 |
|---|---|
| ER模型与规范化 | 如果ER图设计的好,应该无需过多的规范化,以大学数据库为例: |
| 若在instructor中包含了属性dept_name和dept_address,且又有依赖dept_name->dept_address,就一定需要规范化 |
如果在ER设计时创建department,instructor和二者间的联系集合,就无需额外规范化 |
| | 注意,二元以上联系集可能使得模式不属于期望得范式
总结:规范化既可以在建模时靠分析实现,也可以对于现有模型进行规范化 |


