Ch2 随机变量及其分布

1. 随机变量及其分布函数

首先区分三个概念:

• 随机变量:随机变量用于说明随机试验可能结果与数之间的关系,毕竟随机试验需要和数学先建立联系

• 随机变量的概率分布:概率分布是随机变量所有可能结果及其相应概率的列表 :::info 在下面的离散和连续型随机变量中他们的概率分布意义有所不同:
  (1)离散型:概率分布(概率质量函数),也叫分布律,其对应某个x的输出结果就是P(X=x)
  (2)连续型:概率密度函数,但是其结果不等于概率,概率必须要求fx的区间积分 :::

• 分布函数F(x):函数允许我们简洁地定义一个概率分布,避免了列表的繁琐

随机变量分布函数的性质

2. 离散型随机变量及分布

对于离散概率分布，我们关心的是取得一个特定数值的概率。例如抛硬币正面向上的概率为:p(x=正面)=1/2
概率分布(概率质量函数)
离散型随机变量的概率分布主要有三种形式,都描述了随机变量取某个离散值时的概率:

分布函数
概率分布函数是一个普通的实函数,用于表示“X取值不超过x的概率”

常见离散型分布
当统计学家们开始研究概率分布时,有几种形状反复出现,于是就研究他们的规律,根据这些规律来解决特定条件下的问题,这就是为什么会产生许多知名的随机变量分布

分布	表示	概率分布	分布函数	实际应用
几何分布				可列重伯努利试验中,事件A首次发生在第k次的概率
超几何分布				N个球的袋中,其中m个红球,求一次性模n个小球,里面有恰好k个红球的概率
二项分布				n重伯努利试验中,事件A发生k次的概率: N个球的袋中,其中m个红球,摸n次,每次1个球,摸完放回,求n次后恰好摸出k次红球概率
0-1分布				n=1的n重伯努利试验,此时X只能取0,1两个值
泊松分布				当n≥50,p≤0.1时,二项分布概率近似等于泊松分布概率

3. 连续型随机变量及分布

而对于连续型概率分布来说，我们无法给出每一个数值的概率，因为我们不可能列举每一个精确数值,我们关注给定变量范围的概率
概率密度函数

:::info 和概率质量函数不同，概率密度函数的输出不是概率值,这是一个极为重要的差别
实际上给定密度函数f(x)后,对f(x)在某一区间的积分才是真正的概率,此时尝试对某一点积分的结果为0:**连续概率分布重要的一个性质是随机变量取得特定结果的概率为0 如下图的阴影面积就是:::

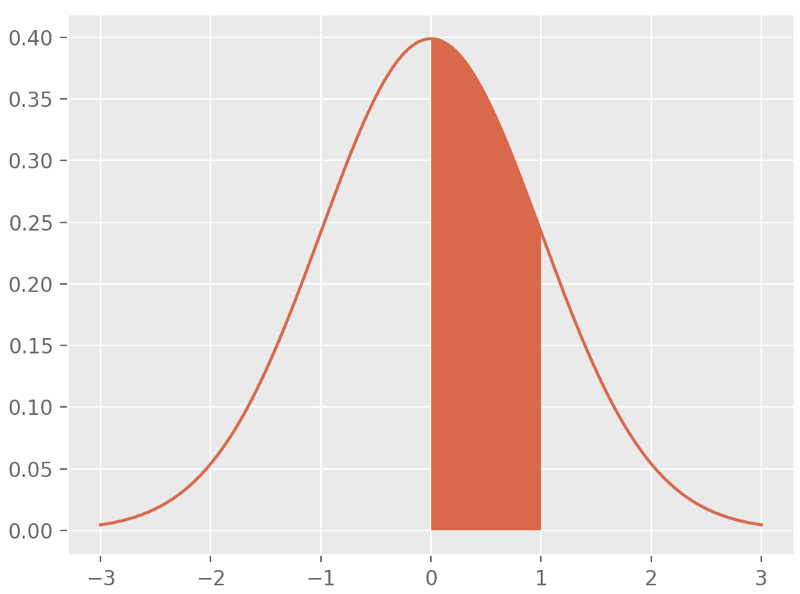
分布函数
通过求密度函数在某一区间的积分得到给定变量范围的概率

重要性质

常见连续型分布

分布	表示	密度函数	分布函数	实际应用
均匀分布				等可能的再区间[a,b]中取值的随机变量,虽然每点被取到的概率相等,但绝不是1/b-a,再次说明连续随机变量取得特定结果的概率为0,求区间积分才能得到概率,其fx和Fx图像如下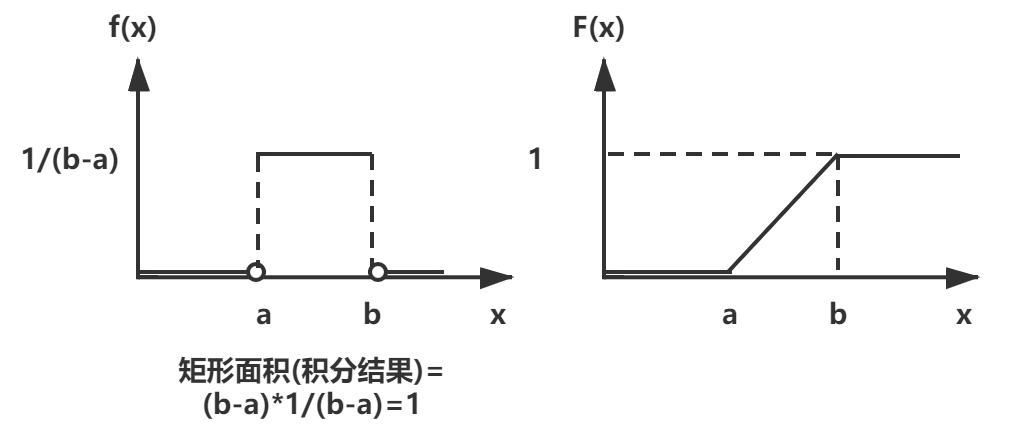
指数分布				指数分布常描述元器件寿命,但其时唯一具有无记忆性的连续型分布:
Γ(Gamma)分布			,有以下性质: 1. 1. 1. 1.

Γ分布常描述元器件或系统寿命,当0<α<1时,失效概率随时间下降,当α>1相反 | |

4. 随机变量函数的分布

一句话:已知X是某个随机变量分布,则y=f(x)的分布就是随机变量函数的分布
离散型

比如已知,则Y的概率分布为
连续型
求连续随机变量函数Y的密度函数流程如下:
已知

5. 例题

例题1: 一维连续随机变量函数的分布

:::info :::