B-树
外部查找成本模型:探查:使用页(计算机中一块连续的数据)的访问次数(无论读写)作为外部查找算法成本模型
B-树
- 定义:作为2-3树拓展,但树由键的副本组成,每个副本关联一条链接,对于M阶B-树
- 每个结点(非根结点)有M/2~M-1对键和链接
- 对比B+树的链接数 = 键数-1
- 根结点个有少于M/2对键和链接,但不能少于2对
- 每个结点(非根结点)有M/2~M-1对键和链接
- 结构特点:M阶B-树(M为正偶数),可能的构成
- 仅一个外部k-结点
- 若干内部k-结点
- 对根结点:k在[2,M-1],对其他结点k在[M/2,M-1]
- 根结点到每个外部结点路径长度相同
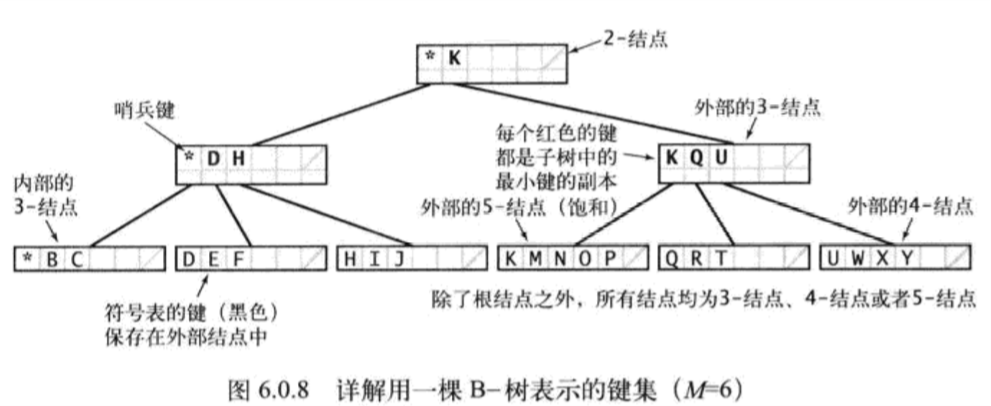
- 结点
- 内部结点:仅保存页相关联键的副本
- 内部结点每个键与一个结点相关联,其子树中的键都大于等于结点关联键,小于内部结点中其余键
- 哨兵键:一个小于所有字符的键,方便查找
- 外部结点:指向实际数据的引用
- 内部结点:仅保存页相关联键的副本
- 操作
- 查找:被查找键存在于集合,查找结束于外部结点,但内部结点遇到被查键后可判断命中并结束,但总会找到对应外部结点
- 与B+树查找区别:B+树查找无论中途是否遇到,不能保证外部一定有查找键
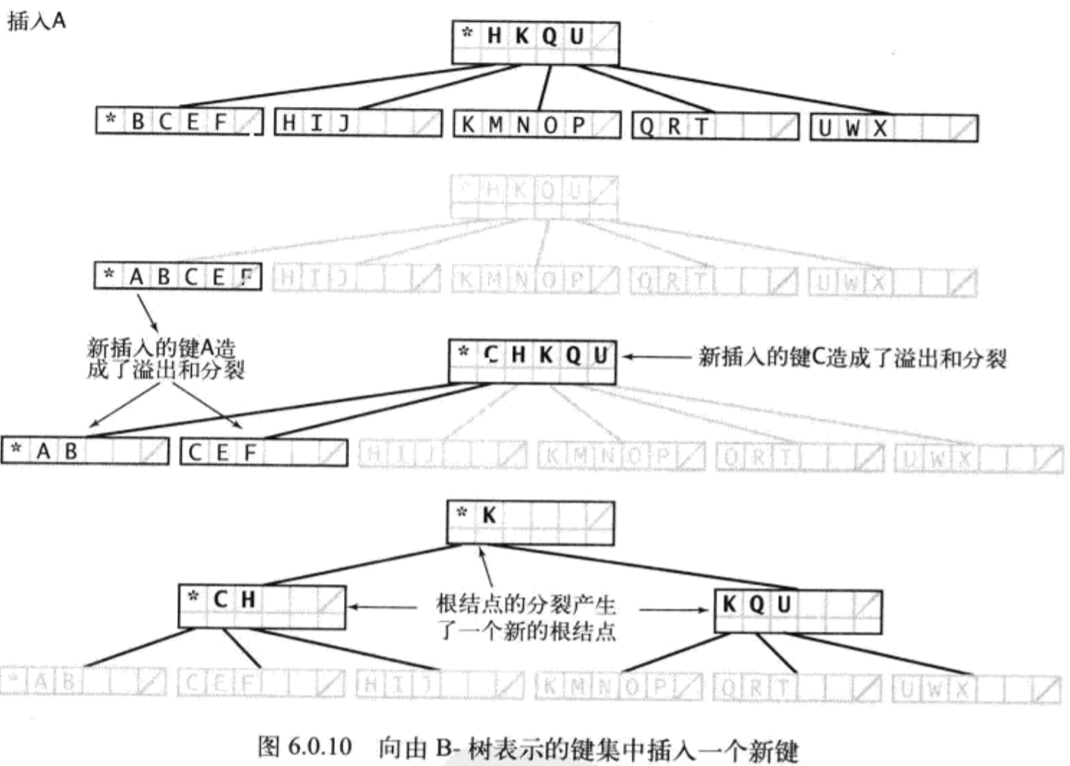
- 插入:即查找未命中,到达树底,插入新键
- 当空间不足,则需要将其分裂,更新内部结点副本,若内部结点空间也不足,继续分裂直到根结点
- 查找:被查找键存在于集合,查找结束于外部结点,但内部结点遇到被查键后可判断命中并结束,但总会找到对应外部结点
B-树的页API: public class Page
| 返回类型 | 方法 | 描述 |
|---|---|---|
| void | add(Key key) | 键插入外部页 |
| void | add(Page p) | 打开内部页,向其中插入条目并关联p和p中最小键 |
| boolean | isExternal() | 是否为外部页 |
| boolean | contains(Key key) | key是否在页中 |
| Page | next(Key key) | 可能含有key的子树 |
| Page | spilt() | 将较大键移动到新页 |
- 对于contains()
- 当前为外部页,key在页中——返回true
- 当前为外部页,key不在页中——返回false
- 否则,递归在子树寻找
B-树集合实现
public class BTreeSET<Key extends Comparable<Key>>{//初始化private Page root = new Page(true);public BTreeSET(Key sentinel){ add(sentinel);}//查找public boolean contains(Key key){return contains(root, key);}private boolean contains(Page h, Key key){if(h.isExternal()) return h.contains(key);//判断外部页是否含有键return contains(h.next(key), key);//子树递归}//插入public void add(Key key){add(root, key);if(root.isFull()){//结点已满Page lefthalf = root;Page righthalf = root.spilt();//分裂root = new Page(false);root.add(lefthalf);root.add(righthalf);}}public void add(Page h, Key key){if(h.isExternal()){ h.add(key); return;}//抵达外部页,添加结点Page next = h.next(key);add(next, key);//否则继续递归向下if(next.isFull)//当外部结点已满,向上分裂h.add(next.spilt());next.close();//关闭页}}
算法分析
- N个元素的M阶B-树一次查找或插入需要logN~logN次探查
最好情况下生成M-1向完全树,最坏时,根结点只有两个链接指向两棵M/2向完全树

