Ch9 假设检验

1. 基本思想

假设检验的思想是给定总体的样本,提出有关总体的假设,使用样本的信息判断假设是否成立 :::info


:::

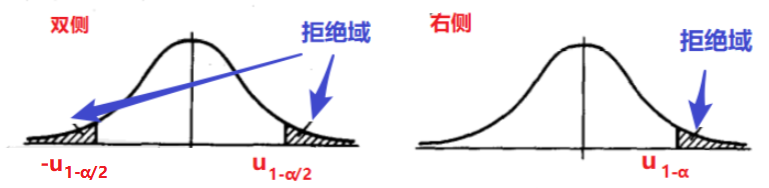
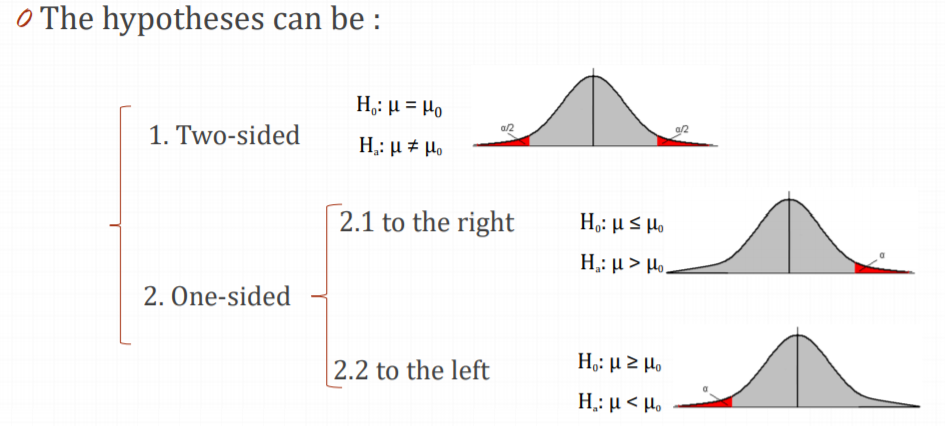
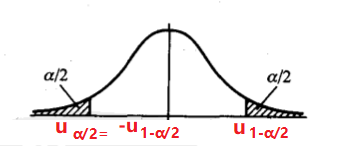
1.1 双侧检验

1.2 单侧检验

小结

1.3 两类错误

• 一类:弃真,H0确实正确,但检验统计量落入拒绝域,因此拒绝了H0,概率记为α,即显著性水平
• 二类:取伪,H0确实错误,但检验统计量的值未落入拒绝域,因此没有拒绝H0,概率记为β | 4种可能及概率 | | 事实 | | | :—-: | :—-: | —- | —- | | | H0真 | H1真 | | 决策 | 拒绝H0 | 第Ⅰ类错误,α | 正确,1-β | | | 不拒绝H0 | 正确1-α | 第Ⅱ类错误,β |

1.4 假设检验的一般步骤

:::info (1)根据问题确定假设H0和H1
(2)根据已知条件选择合适检验统计量U
(3)根据显著性水平α,查表确定临界值
(4)根据观测值计算检验统计量得观测值,和临界值比较,再对假设判断 :::

2. 正态总体下参数的假设检验

需要根据已知条件**选择合**适检验统计量U

2.1 一个正态总体

2.2 两个正态总体

:::danger 对比Ch8 区间估计可以发现相同总体和未知参数的情况下,样本函数与检验统计量形式类似.

• 区间估计是未知参数值时,估计在给定可靠程度下参数值可能的误差范围
• 假设检验是已知观测值下的参数值,判断它是否落入给定可靠程度下可接收的误差范围中(接受域) :::