Ch8 参数估计

总体X的分布函数中可能有未知参数或未知参数向量θ,此时记总体分布函数

利用**样**本了解未知参数/参数向量θ即为参数估计

1. 点估计

• 估计值和估计量统称为θ的一个点估计
• 点估计量是一个统计量,因此是随机变量

• 点估计值是一个实数,点估计值和点估计量可同时记为

  1.1 矩估计法

  使用k阶样本原点矩代替k阶总体原点矩进行估计

• 一阶

• 二阶(黑粗体θ为向量)

** :::info
:::

• k阶

1.2 极大似然估计法

假设当前样本观测值发生概率为所有可能结果中发生概率最大的
:::info 首先了解”似然函数(Likelihood function)”:统计学中,似然函数是一种关于统计模型参数的函数:给定输出x时,关于参数θ的似然函数L(θ|x)(在数值上)等于给定参数θ后变量X的概率,即

由上定义
:::

2. 估计量的评选标准

3. 区间估计

点估计的结果点估计值是一个实数,而我们知道一般的估计都有误差,只是误差范围不好确定.区间估计的思想就是指定一个概率,在这个可靠程度下计算估计值可能的误差范围.

下面是θ区间估计问题解法步骤: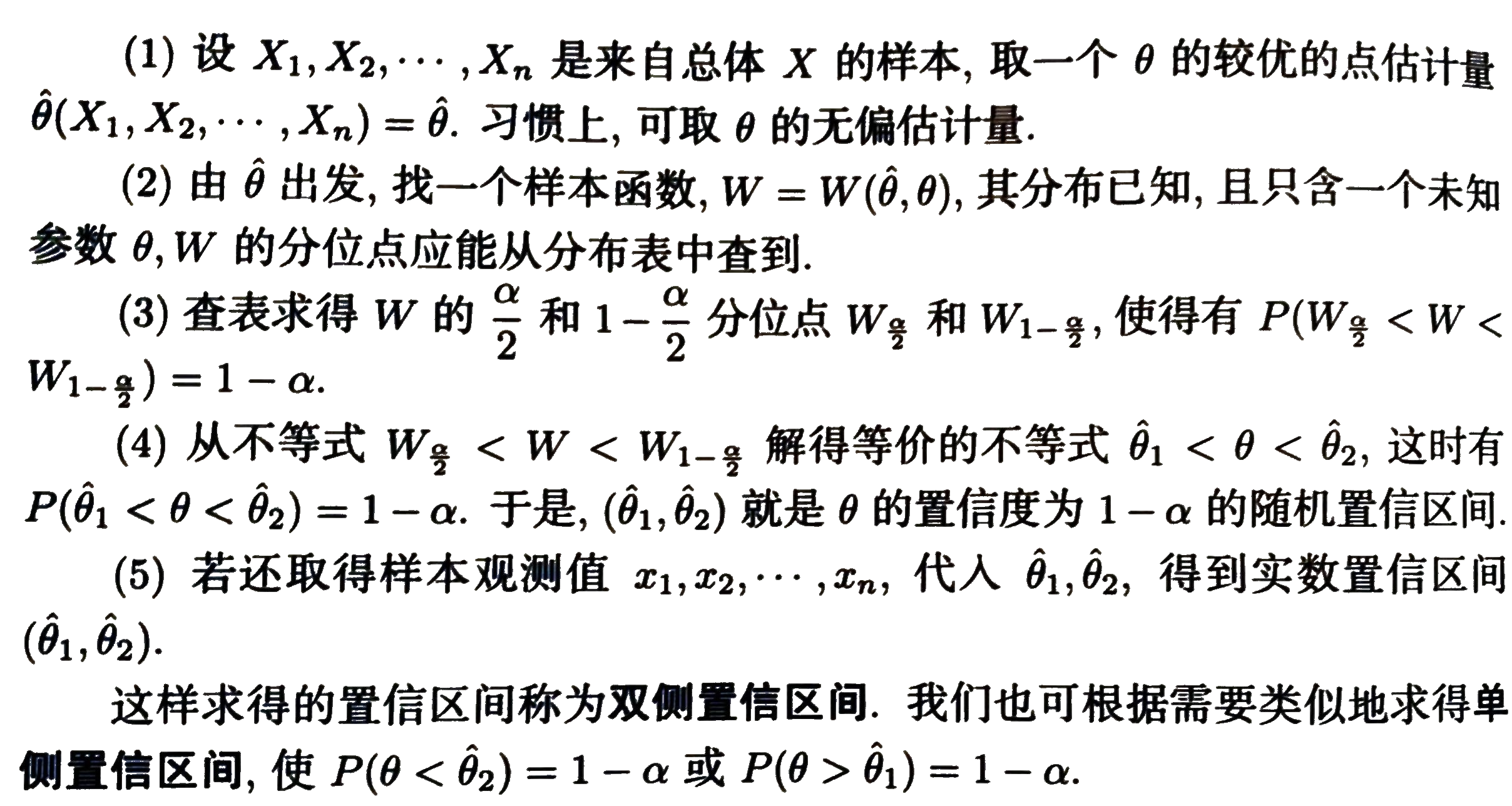

接下来讨论正态总体下参数的区间估计

3.1 一个正态总体下的区间估计

下方选择样本函数时要根据条件使得样本函数中只能有一个未知量θ

条件	样本函数与分布	概率式&分位点不等式&置信区间	图像

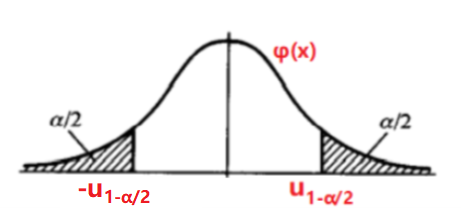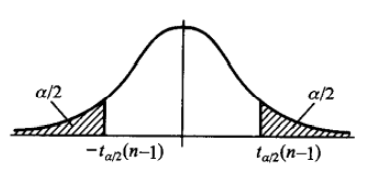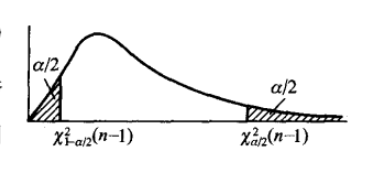3.2 两个正态总体下的区间估计

                13216543219865432