算法4.10 无环加权有向图的SP算法

算法4.10 无环加权有向图的SP算法

算法描述

• Dijkstra算法中使用pq.delMin()保证了每个结点v只会放松一次,但操作pq开销较大,在无环加权有向图中,拓扑排序也能保证每个顶点只会放松一次

实现

public class AcyclicSP {
    private DirectedEdge[] edgeTo;
    private double[] distTo;
    public AcyclicSP(EdgeWeightedDigraph G, int s){
        edgeTo = new DirectedEdge[G.V()];
        distTo = new double[G.V()];
        for (int v = 0; v < G.V(); v++)
            distTo[v] = Double.POSITIVE_INFINITY;
        distTo[s] = 0.0;
        Topological top = new Topological(G);//根据DAG建立拓扑排序
        for (int v:top.order()) relax(G,v);
    }
    private void relax(EdgeWeightedDigraph G, int v){
        for (DirectedEdge e: G.adj(v)){
            int w = e.to();
            if (distTo[w] > distTo[v]+e.weight()){
                distTo[w] = distTo[v]+e.weight();
                edgeTo[w] = e;
            }
        }
    }
    public double distTo(int v){}//s->v的距离
    public boolean hasPathTo(int v){}
    public Iterable<DirectedEdge> pathTo(int v){}
}

算法分析

• Topo顺序在E+V成正比时间内生成,则解决SP问题也与次成正比
• Topo顺序与边的权重正负无关,则可以解决负权重的最短路径问题

无环加权有向图的最长路径LP算法

算法描述

• 将图中G的边权重取相反数,求得最短路径即为最长路径

实现

可以不取相反数,采用等价但更简单的方式

1. distTo[]都初始化为NEGATIVE_INFINITY
2. >变为<,distTo[w] < distTo[v]+e.weight()时放松顶点.

-1.8 < -2.0 + 0.3时将distTo[w]增大为-1.7,即v->w比原来的edgeTo[w]权重大,LP问题中distTo[w]只会变大,与SP问题恰好相反

算法分析

• 同算法4.10,都与E+V成正比

并行任务调度问题

• 优先级限定的任务调度:只考虑一件任务发生的前提任务,最终产生Topo排序
  • 优先级限定+并行调度:在满足优先级的情况下,尽可能同时完成无优先级冲突的任务,从而在最短时间内结束
    • 思考:尽早安排每一个任务
      • 建模:关键路径:等价于加权有向无环图的最长路径问题:Topo顺序保证了任务的先来后到,distTo[]理解为timeToDo[],只能增大或不变(实现中weight=0.0时,表示可并行处理,时间不计),因为不可能Topo排序中后面的任务先于前面的任务完成.
      • 正确性证明: 把根据Topo顺序放松结点的最长路径理解为满足优先级限定下一项一项完成任务,但优先级限定边的权值为0即忽略了可并行任务的用时,综上关键路径即完整任务的最优选择

示例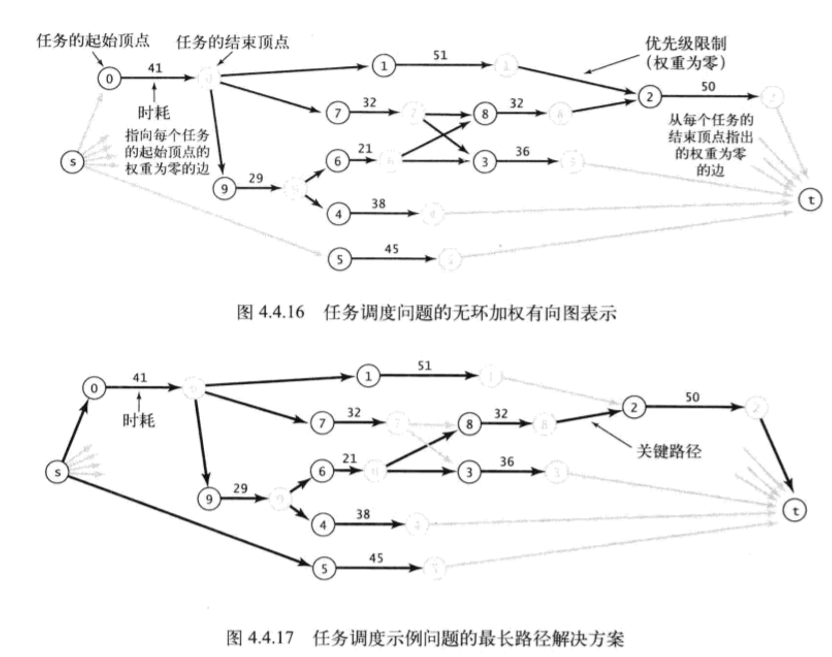

实现:CPM类

• 构造加权DAG,起点s,终点t,其中一个任务对应一个起始点v.start,一个完成点v.end,N个任务,则G(2N+2,E),对于有先后限定的任务v->w,addEdge(v.end,w.start,0.0),对每个任务的自身addEdge(v.start,v.end,time)
• 每个任务的开始时间即为起点s到v.start点的dist