时间复杂度

时间复杂度(Asymptotic Complexity)被用来估算程序运行的开销,常见复杂度如下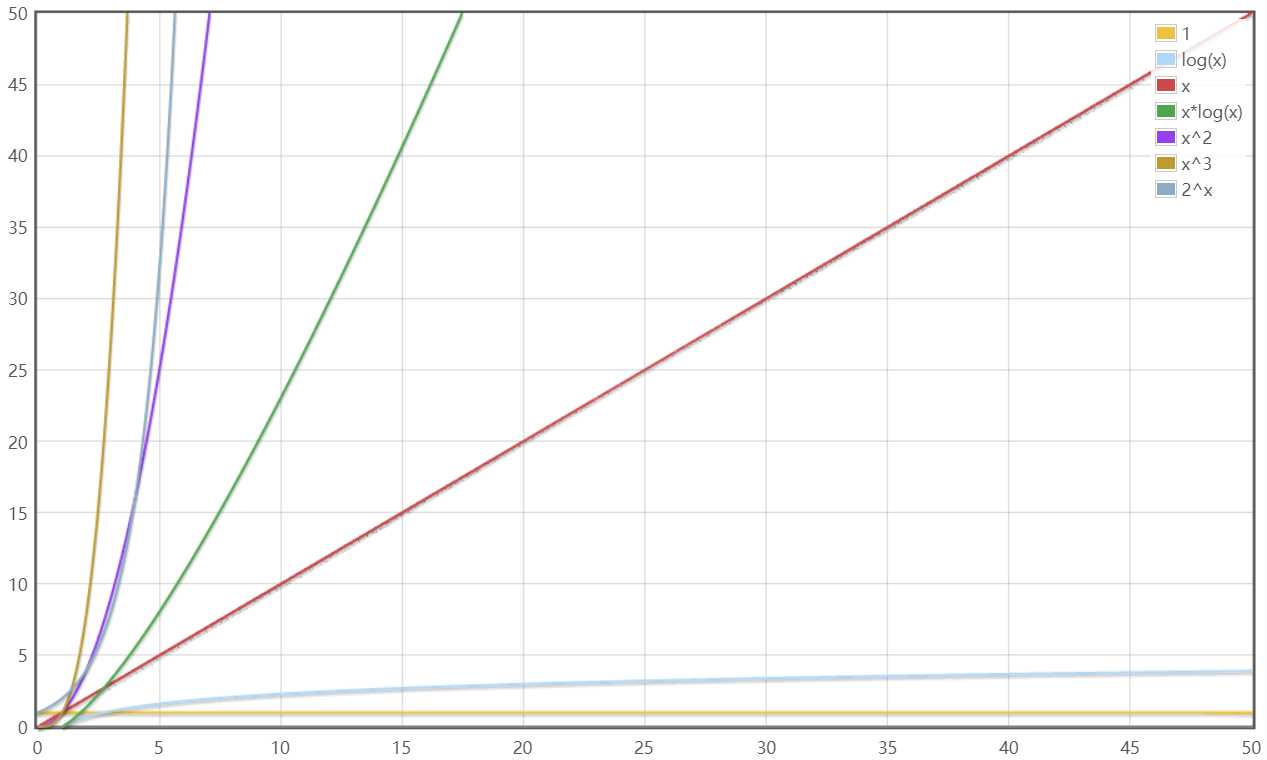
Ch10 程序性能优化 - 图1

常见复杂度和场景

描述 增长的数量级 说明 举例
常数 O(n) 普通语句 两数相加
对数 O(logN) 二分策略 二分查找
线性 O(N) 循环 找出最大值
线性对数 O(NlogN) 分治 归并排序
平方 O(N²) 双层循环 检查所有元素对
立方 O(N³) 三层循环 检查所有三元组
指数 O(2) 穷举查找 检查所有子集

优化编译器的局限

内存别名

程序中两个不同名指针变量可指向相同地址,被称为内存别名(memory aliasing),此时某些优化会带来不同的结果

  • (GCC为例)编译器在优化时会假设存在内存别名的情况

示例程序

  1. //优化前,需4读2写
  2. void fun() {
  3.     int a = 1;
  4.     int* p = &a;
  5.     int* q = &a;
  6.     *p += *q;
  7.     *p += *q;
  8.     //结果a = 4
  9. }
  10. //优化后,需2读1写
  11. void fun() {
  12.     int a = 1;
  13.     int* p = &a;
  14.     int* q = &a;
  15.     *p += 2 * *q;
  16.     //结果a = 3
  17. }

上述程序中当p和q同时指向a的空间,此时合并运算会产生完全不同的结果,编译器必须假设存在这种情况

函数副作用

某些时候调用函数会产生一些意料之外的效果

  • 编译器需假设每次调用函数都会有副作用(side-effects)

示例程序

  1. //全局变量
  2. int counter = 0;
  3. int f(int x){
  4.     return counter++;
  5. }
  7. //优化前
  8. int func1(x){
  9.     return f(x) + f(x) + f(x) + f(x);
  10. }
  11. //优化后
  12. int func2(x){
  13.     return 4*f(x);
  14. }

func1若被优化为func2,看似合理,但如果每次调用f()会改变一次全局变量,则优化后产生副作用

CPE

定义 每元素的周期数(Cycles Per Element, CPE),用于度量具有“在一组元素上迭代的循环”程序的性能
周期 CPU活动由时钟控制,时钟提供规律信号,即”时钟周期”,单位一般为千兆赫兹(GHz),即每秒钟十亿(10)周期.而每周期时间即频率的倒数,如4GHz处理器的周期时间为0.25纳秒
元素 迭代循环中的一类数据中的对象,如数组元素

举例,下列为一个向量计算程序,psum1()每次计算一个元素,psum2()每次计算两个元素

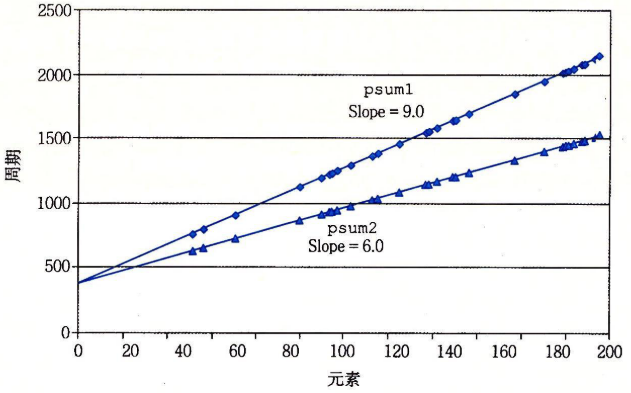image.png 拟合效果如下

image.png
psum1=>368+9.0n
psum2=>368+6.0n

分析:

  • 起始值368:说明函数的准备,初始化,完成阶段需368周期
  • 斜率:即CPE

psum1()计算每个元素周期开销为9
psum2()计算每个元素周期开销为6

常用优化

代码移动(code motion)
把把循环中每次都计算但值都不变的操作移出循环
减少过程调用
比如caller直接使用数组元素,而非通过callee获取元素值后返回给caller
减少不必要引用
在某些循环中,把当前结果保存在临时变量中最后写入,比每次都更新目标内存要高效
循环展开
循环展开(Loop Unrolling),通过增加每次迭代计算的元素数量减少总共所需的循环次数.
如上psum2()使用了2×1循环展开
提高并行性, 常量折叠 … …

选择题知识点

  1. 对于大部分时候都在比较字符串的程序,使用什么方法可以最大提高性能?

对每个字符串使用独立的指针,这样直接使用指针比较即可

  1. 下列函数可进行”减少过程调用”优化:使用temp变量保存s[i],而非每次访问数组 ```c void lower1(char *s) { int i; for (i = 0; i < strlen(s); i++) if (s[i] >= ‘A’ && s[i] <= ‘Z’) s[i] -= (‘A’ - ‘a’);

}( ```

  1. 从程序运行速度上优化程序可以:使用更快的算法,与占用空间和指针无关
  2. 为了优化程序,需要①找到hot spot②理解程序运行时的处理器特性,无需了解所有系统调用
  3. 下列有关C程序优化的说法,正确的是: 全错

①只需要配置优化模式即可②无需理解CPU特性③无需关注汇编代码