Ex2_2_11归并排序优化

优化一:加快小数组排序:

递归会使小规模问题中的方法调用过于频繁,可以规定,当lo和hi的差值小于某一阈值时就改用插入排序,只需要替换一句话

  1. //if (hi <= lo) return;
  2.     if (hi - lo <= 15) {
  3.         Insertion(src, lo, hi);
  4.         return;
  5.     }

优化二:测试数组是否已经有序:

可以增加一个判断,如果a[mid]<=a[mid+1]则认为数组已经是有序的(以为此时左右两部分已经是排好序的),并跳过merge()方法,此时任意有序子数组算法运行时间就变成了线性的.

  1. if (less(aux[mid], aux[mid + 1])) {
  2.             System.arraycopy(aux, lo, src, lo, hi + 1 - lo);//如果已经有序,只需复制过来就好
  3.             return;
  4.         }
  5.         merge(src, aux, lo, mid, hi);

优化三:不将元素复制到辅助数组:

原来merge()方法是将原数组src复制一份到aux后,再将aux的元素按顺序归并回src,但可以优化这一步,节省将数组元素复制到aux的时间(但空间不行),这需要在递归的每层交换输入数组和辅助数组的参数位置

  1. private static void sort(Comparable[] src, Comparable[] aux, int lo, int hi) {
  2.         //if (hi <= lo) return;
  3.         if (hi - lo <= 15) {
  4.             Insertion(src, lo, hi);
  5.             return;
  6.         }
  7.         int mid = lo + (hi - lo) / 2;
  8.         sort(aux, src, lo, mid);//交换角色
  9.         sort(aux, src, mid + 1, hi);
  10.         if (less(aux[mid], aux[mid + 1])) {
  11.             System.arraycopy(aux, lo, src, lo, hi + 1 - lo);//如果已经有序,只需复制过来就好
  12.             return;
  13.         }
  14.         merge(src, aux, lo, mid, hi);//保持原顺序,确保最终是src被排好序
  15.     }

完整代码

  1. import edu.princeton.cs.algs4.In;
  2. import edu.princeton.cs.algs4.StdOut;
  4. public class Ex2_2_11 {
  5.     private static Comparable[] aux;
  7.     private static boolean less(Comparable v, Comparable w){
  8.         return v.compareTo(w) < 0;
  9.     }//比较v是否小于w
  11.     public static void sort(Comparable[] src){
  12.         aux = src.clone();
  13.         sort(src, aux,0, src.length-1);
  14.     }
  16.     private static void sort(Comparable[] src, Comparable[] aux, int lo, int hi) {
  17.         //if (hi <= lo) return;
  18.         if (hi - lo <= 15) {
  19.             Insertion(src, lo, hi);
  20.             return;
  21.         }
  22.         int mid = lo + (hi - lo) / 2;
  23.         sort(aux, src, lo, mid);//交换角色
  24.         sort(aux, src, mid + 1, hi);
  25.         if (less(aux[mid], aux[mid + 1])) {
  26.             System.arraycopy(aux, lo, src, lo, hi + 1 - lo);//如果已经有序,只需复制过来就好
  27.             return;
  28.         }
  29.         merge(src, aux, lo, mid, hi);//保持原顺序,确保最终是src被排好序
  30.     }
  32.     private static void merge(Comparable[] src, Comparable[] aux, int lo, int mid, int hi){
  33.         int i = lo;
  34.         int j = mid + 1;
  36. //        少了复制到辅助数组的步骤
  37. //        for(int k = lo; k <= hi; k++){
  38. //            aux[k] = a[k];
  39. //        }
  41.         for(int k = lo; k <= hi; k++){
  42.             if(i > mid) src[k] = aux[j++];
  43.             else if(j > hi) src[k] = aux[i++];
  44.             else if(less(aux[j],aux[i])) src[k] = aux[j++];
  45.             else src[k] = aux[i++];
  46.         }
  47.     }
  49.     private static void Insertion(Comparable[] a, int lo, int hi){
  50.         for(int i = lo+1; i <= hi; i++){
  51.             for(int j = i;  j > lo && less(a[j],a[j-1]); j--){
  52.                 exch(a,j,j-1);
  53.             }
  54.         }
  55.     }
  56.     private static void exch(Comparable[] a, int i, int j){
  57.         Comparable t = a[i];
  58.         a[i] = a[j];
  59.         a[j] = t;
  60.     }//元素交换
  62.     private static void show(Comparable[] a){
  63.         for(int i = 0; i < a.length; i++)
  64.             StdOut.print(a[i] + " ");
  65.         StdOut.println();
  66.     }
  68.     public static void main(String[] args){
  69.         String[] a = In.readStrings();
  70.         sort(a);
  71.         show(a);
  72.     }
  73. }

src和aux交替角色示意以及分治思想

如图所示,只要第一次sort时顺序正确,最终一定对应merge使得src有正确排序(911,910代表不同地址的两个数组)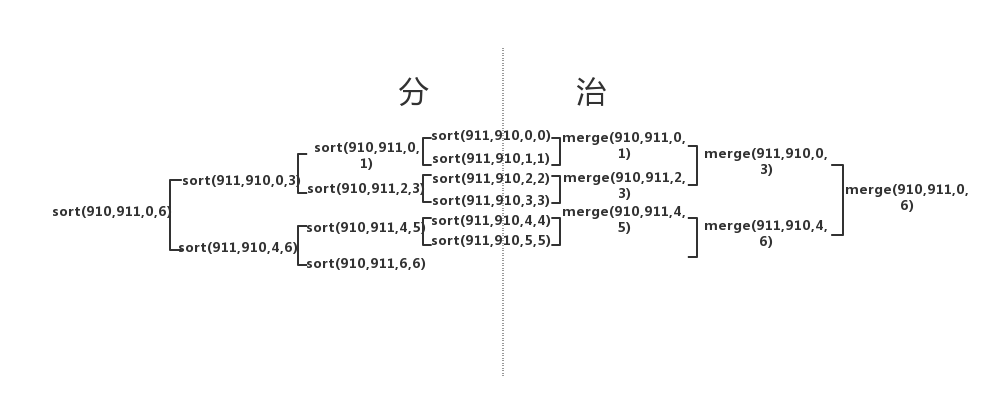
分治法.jpg

Review:

  1. 避免复制到辅助数组:
    前提是sort(Comparable[] src)中执行aux = src.clone(),aux[]先进行克隆.在重载sort(Comparable[] src,Comparable[] aux, int lo, int hi)中,aux要作为参数传入,交换传参针对两个sort()和arraycopy(),merge()中aux和src顺序不变.
  2. 检测是否已有序:
    若有序,则使用语句System.arraycopy(aux, lo, src, lo, hi+1-lo).
    该函数对于数组是深拷贝(两个引用指向不同的数组对象),对于数组内的对象是浅拷贝(数组对象中存放的不同对象引用实际指向一个堆上的对象).因为操作的传入参数是数组,那么回归本意,效果是深复制.