一元：仅有一个自变量
解释：一个因素只受到另一个因素的影响的规律
公式：

1.准备数据

生成X轴序列

import numpy as np
t=np.arange(1,10,1)
t

array([1, 2, 3, 4, 5, 6, 7, 8, 9])

生成Y轴序列

y=0.9+t+np.sin(t)
y

array([ 2.74147098,  3.80929743,  4.04112001,  4.1431975 ,  4.94107573,
        6.6205845 ,  8.5569866 ,  9.88935825, 10.31211849])

2.可视化

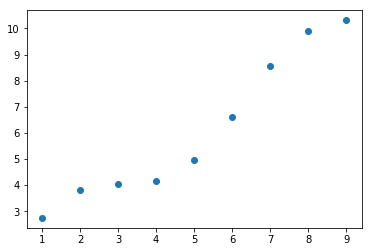
用于数据探索：初步认定是不是一阶线性方程。

import matplotlib.pyplot as plt
plt.plot(t,y,'o')
plt.show()

3.建模

model=np.polyfit(t,y,deg=1)  
model

array([1.00053154, 1.11458778])
模型：

4.预测

X值

t2=np.arange(-2,12,0.5)
t2

array([-2. , -1.5, -1. , -0.5,  0. ,  0.5,  1. ,  1.5,  2. ,  2.5,  3. ,
        3.5,  4. ,  4.5,  5. ,  5.5,  6. ,  6.5,  7. ,  7.5,  8. ,  8.5,
        9. ,  9.5, 10. , 10.5, 11. , 11.5])

Y值

y2predict=np.polyval(model,t2)
y2predict

array([-0.88647531, -0.38620954,  0.11405623,  0.61432201,  1.11458778,
        1.61485355,  2.11511932,  2.61538509,  3.11565087,  3.61591664,
        4.11618241,  4.61644818,  5.11671395,  5.61697973,  6.1172455 ,
        6.61751127,  7.11777704,  7.61804281,  8.11830859,  8.61857436,
        9.11884013,  9.6191059 , 10.11937167, 10.61963745, 11.11990322,
       11.62016899, 12.12043476, 12.62070053])

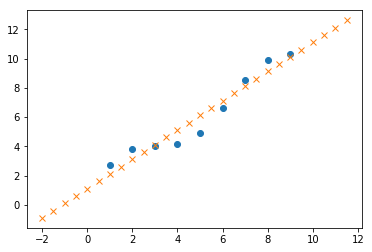
可视化

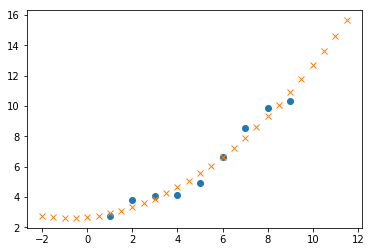
plt.plot(t,y,'o',t2,y2predict,'x')
plt.show()

5.模型优化

参数调整：deg

model=np.polyfit(t,y,deg=2)   #  
model

array([0.08528185, 0.147713 , 2.67808844])
模型：