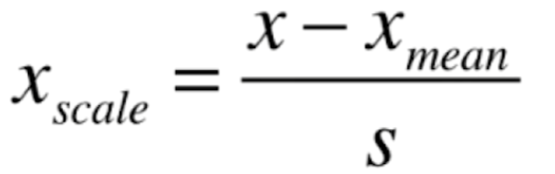为什么归一化

将每个特征的影响“公平化”。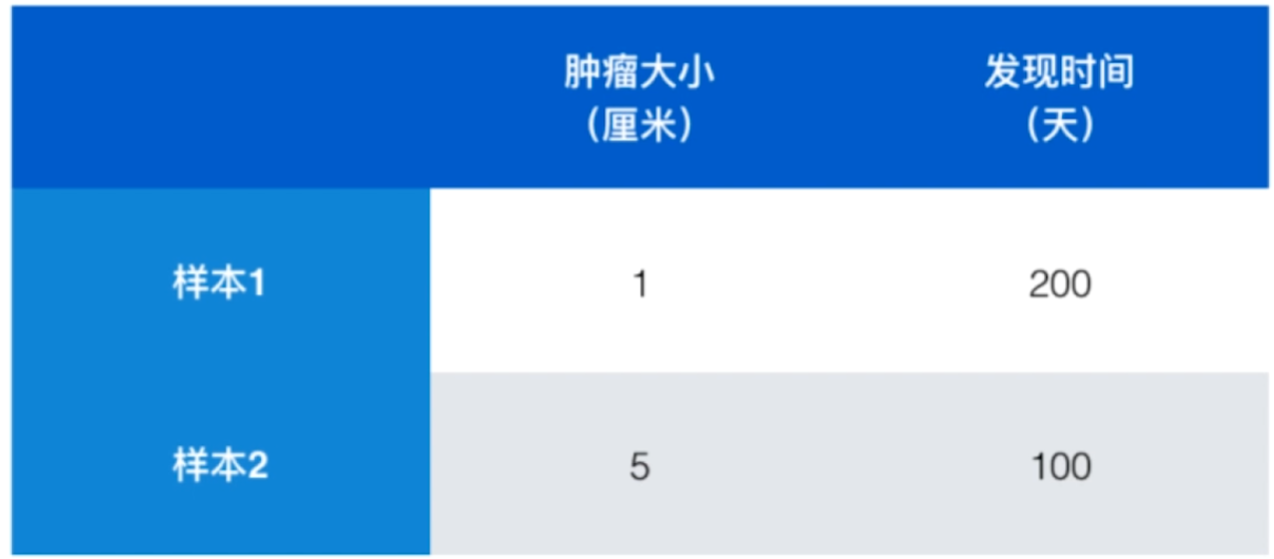

由于“发现时间”的数值是两位数，“肿瘤大小”的数值是个位数，在KNN算法进行“距离”运算后，很明显特征“发现时间”的影响比特征“肿瘤大小”更大，如何消除这种不同数值规模带来的“不公平”呢？

解决方法

将所有的数据映射到同一尺度。

最值归一化

把所有数据映射到 0-1 之间。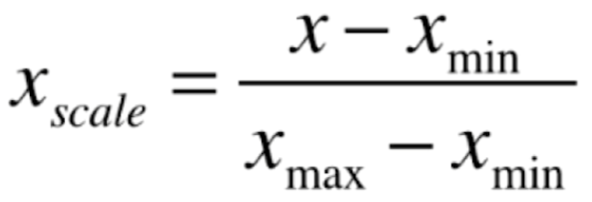

• 局限性：适用于分布有明显边界的情况。

• [x] 缺点：受outlier影响较大。

  均值方差归—化

• [x] 算法思想：把数据平移(到坐标原点附近)、压缩(把数据)

• 原理：把所有数据归一到均值为0方差为1的分布中。
• 优点：相比最值归一化，没有了其局限性和缺点。

编码

import numpy as np
import matplotlib.pyplot as plt
# 准备数据：50行 * 2列的矩阵
X2 = np.random.randint(0, 100, (50, 2))
X2 = np.array(X2, dtype=float)
# 每列均值方差归—化
X2[:,0] = (X2[:,0] - np.mean(X2[:,0])) / np.std(X2[:,0])
X2[:,1] = (X2[:,1] - np.mean(X2[:,1])) / np.std(X2[:,1])
# 可视化
plt.scatter(X2[:,0], X2[:,1])
plt.show()

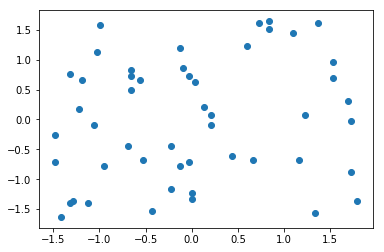
# 特征1的：均值、方差
np.mean(X2[:,0])  # -1.1102230246251565e-16
np.std(X2[:,0])  # 0.9999999999999999
# 特征2的：均值、方差
np.mean(X2[:,1])  # 1.121325254871408e-16
np.std(X2[:,1])  # np.std(X2[:,1])

公式

在自然界中，大部分的数据都是符合正态分布的。
从这个角度得到启发，进行数据量纲的统一。(其实量纲统一的方式有很多)

将一个标准正态分布转化为一个普通正态分布，公式如下：

其中，为标准正态分布中的元素，为平均值，S 为标准差。
如何理解？

• 1.将一个标准正态分布数据样本``放大
• 2.将放大后的数据平移

所以，生成正态分布数据时的代码如下：

data = 2000*np.random.randn (1000) +10000 # 2000为标准差，10000为均值。1000为数据样本数

将上述公式反过来，即为普通正态分布转为标准正态分布

优点

• 1.提高运算效率: 0-1范围内的数值较小，计算机计算快很多。
• 2.减小离群值的影响：数据经过压缩后在一个0-1的范围内，对算法的影响也是微乎其微。

  scikit-learn中的Scaler

  准备数据

  ```python

  源码

  import numpy as np from sklearn import datasets

加载数据

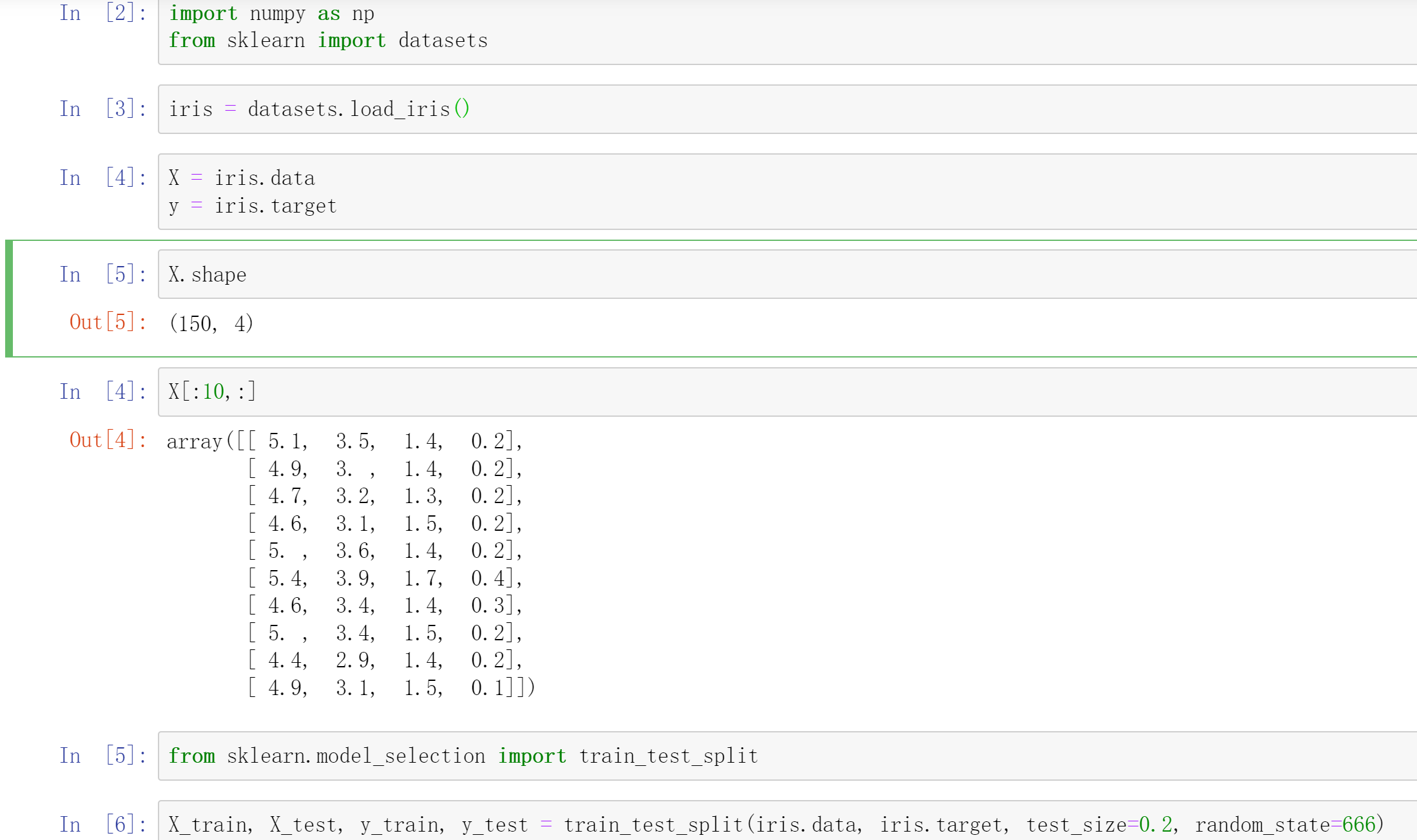
iris = datasets.load_iris() X = iris.data y = iris.target X.shape # (150, 4)

切分数据集

from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=666)

![image.png](https://cdn.nlark.com/yuque/0/2021/png/12405790/1639116343047-4730dd86-ee8c-44d9-919c-f0c5567964b9.png#clientId=u48d78c6f-3017-4&from=paste&height=652&id=u770f98d0&margin=%5Bobject%20Object%5D&name=image.png&originHeight=1304&originWidth=2199&originalType=binary&ratio=1&size=178537&status=done&style=none&taskId=u03036ef3-7308-429d-8071-0e76c0445cb&width=1099.5)
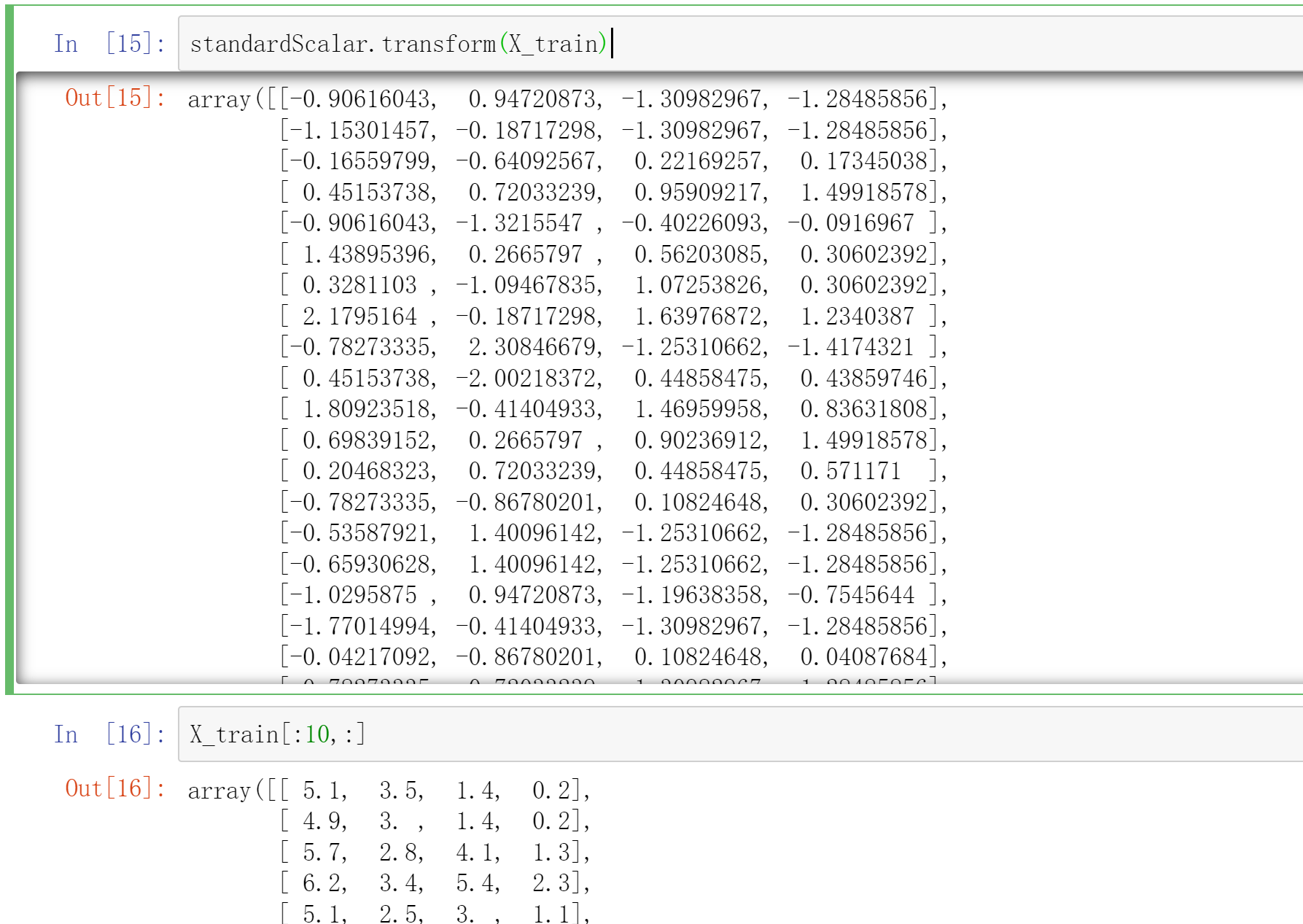
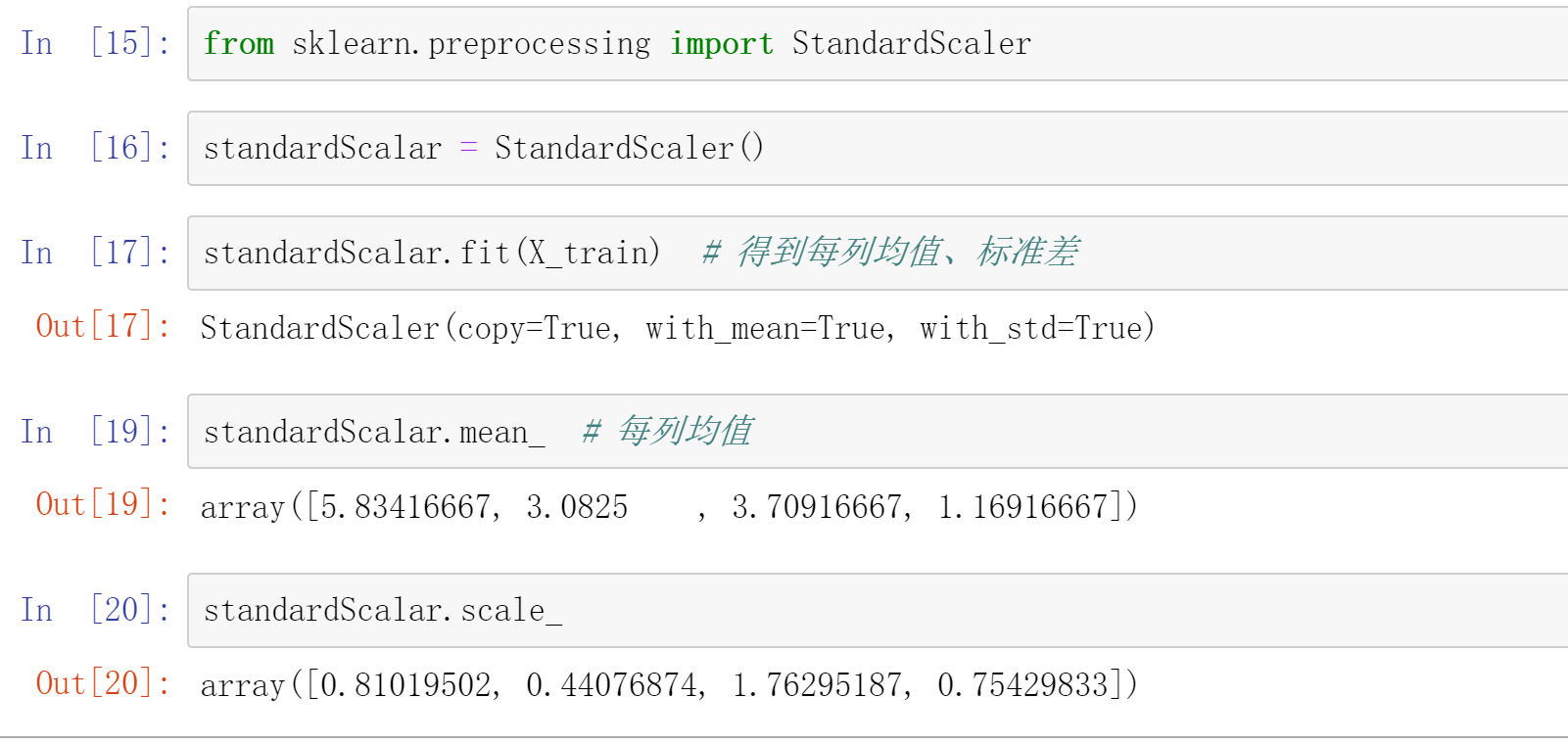
<a name="Eu4II"></a>
## 归一化
```python
# 源码
from sklearn.preprocessing import StandardScaler 
standardScalar = StandardScaler() 
standardScalar.fit(X_train)  # 得到每列均值、标准差
standardScalar.mean_  # 每列均值
standardScalar.scale_  # 每列标准差
standardScalar.transform(X_train)  # 训练集归一化
X_test_standard = standardScalar.transform(X_test)     # 测试集归一化

knn分类

from sklearn.neighbors import KNeighborsClassifier
knn_clf = KNeighborsClassifier(n_neighbors=3)
knn_clf.fit(X_train, y_train)  # 建模
knn_clf.score(X_test_standard, y_test)  # 模型打分
# 如果要预测，特征数据也要归一化

自实现standardScaler

import numpy as np
class StandardScaler:
    def __init__(self):
        self.mean_ = None
        self.scale_ = None
    def fit(self, X):
        """根据训练数据集X获得数据的均值和方差"""
        assert X.ndim == 2, "The dimension of X must be 2"
        self.mean_ = np.array([np.mean(X[:,i]) for i in range(X.shape[1])])
        self.scale_ = np.array([np.std(X[:,i]) for i in range(X.shape[1])])
        return self
    def transform(self, X):
        """将X根据这个StandardScaler进行均值方差归一化处理"""
        assert X.ndim == 2, "The dimension of X must be 2"
        assert self.mean_ is not None and self.scale_ is not None, \
               "must fit before transform!"
        assert X.shape[1] == len(self.mean_), \
               "the feature number of X must be equal to mean_ and std_"
        resX = np.empty(shape=X.shape, dtype=float)
        for col in range(X.shape[1]):
            resX[:,col] = (X[:,col] - self.mean_[col]) / self.scale_[col]
        return resX