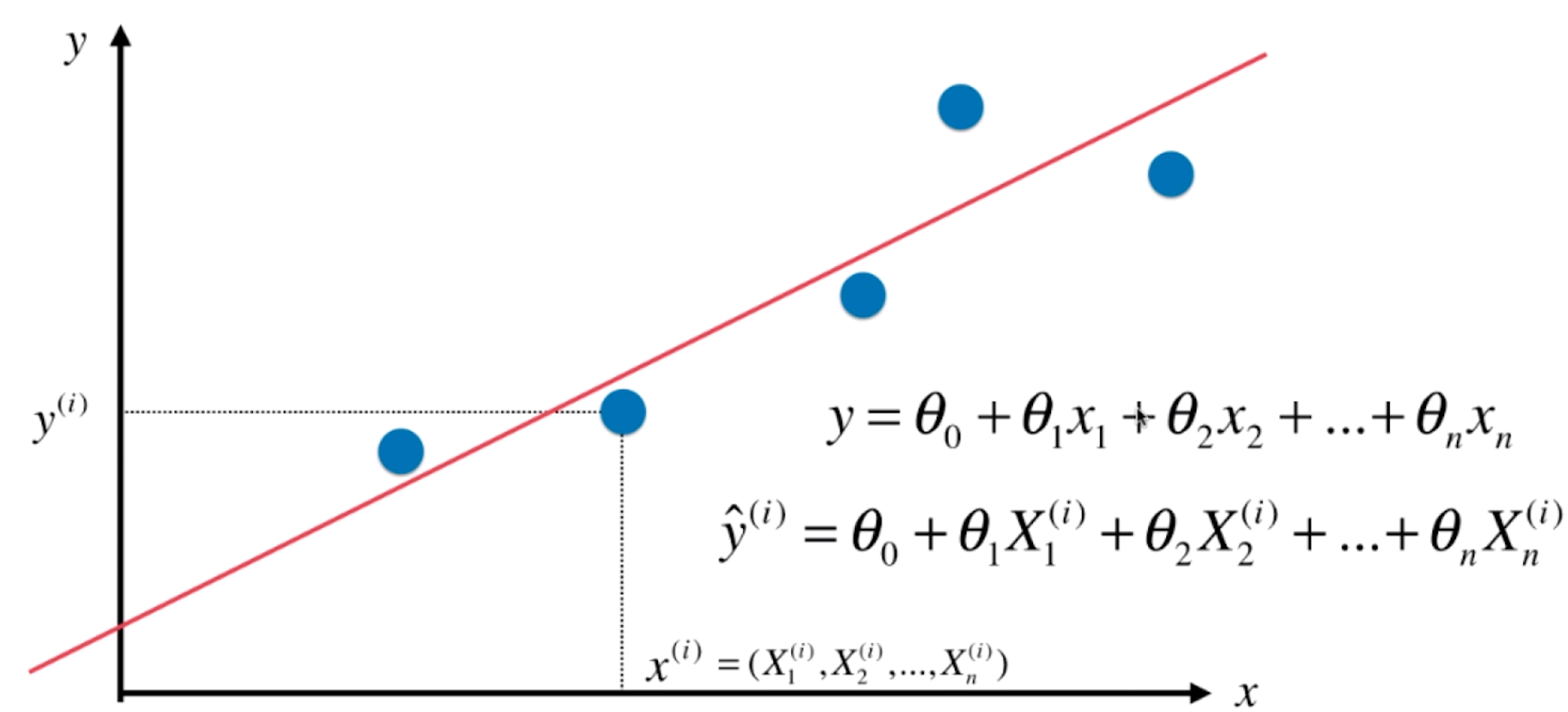
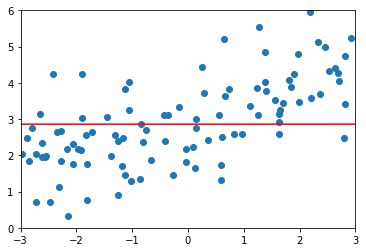
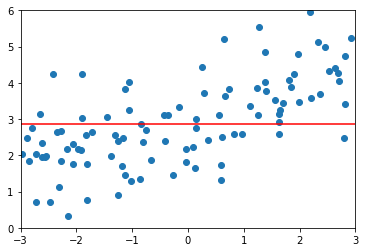
1.2 MSE
Root Mean Squared Errod 均方根误差
这里换一种写法
2.岭回归
2.1 原理
岭回归是模型正则化的一种方式。
目标:使 尽可能小。
这个式子考虑了
的影响,
如果越大,要让整个式子越小,
就应该越小
所以,新的要同时考虑方差和
两个因素,这样就能做到平衡。
- 方差:过拟合,
偏大
- 模型正则化:新的
越小,
越小
2.2 编码
2.2.1 准备数据
```python import numpy as np import matplotlib.pyplot as plt
np.random.seed(42) x = np.random.uniform(-3.0, 3.0, size=100) X = x.reshape(-1, 1) y = 0.5 * x + 3 + np.random.normal(0, 1, size=100)
plt.scatter(x, y) plt.show()
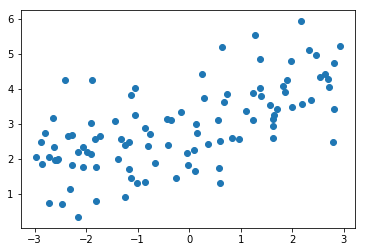<a name="hGZO7"></a>### 2.2.2 多项式建模```pythonfrom sklearn.pipeline import Pipelinefrom sklearn.preprocessing import PolynomialFeaturesfrom sklearn.preprocessing import StandardScalerfrom sklearn.linear_model import LinearRegression# 分割数据from sklearn.model_selection import train_test_splitnp.random.seed(666)X_train, X_test, y_train, y_test = train_test_split(X, y)# 多项式参数配置def PolynomialRegression(degree):return Pipeline([("poly", PolynomialFeatures(degree=degree)),("std_scaler", StandardScaler()),("lin_reg", LinearRegression())])# 建模from sklearn.metrics import mean_squared_errorpoly_reg = PolynomialRegression(degree=20)poly_reg.fit(X_train, y_train)y_poly_predict = poly_reg.predict(X_test)# 衡量MSEmean_squared_error(y_test, y_poly_predict) # 167.94010866878617# 预测X_plot = np.linspace(-3, 3, 100).reshape(100, 1)y_plot = poly_reg.predict(X_plot)plt.scatter(x, y)plt.plot(X_plot[:,0], y_plot, color='r')plt.axis([-3, 3, 0, 6])plt.show()
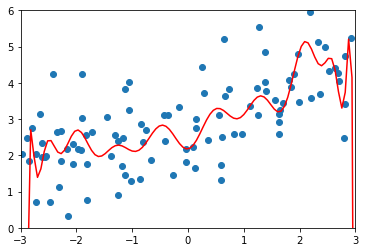
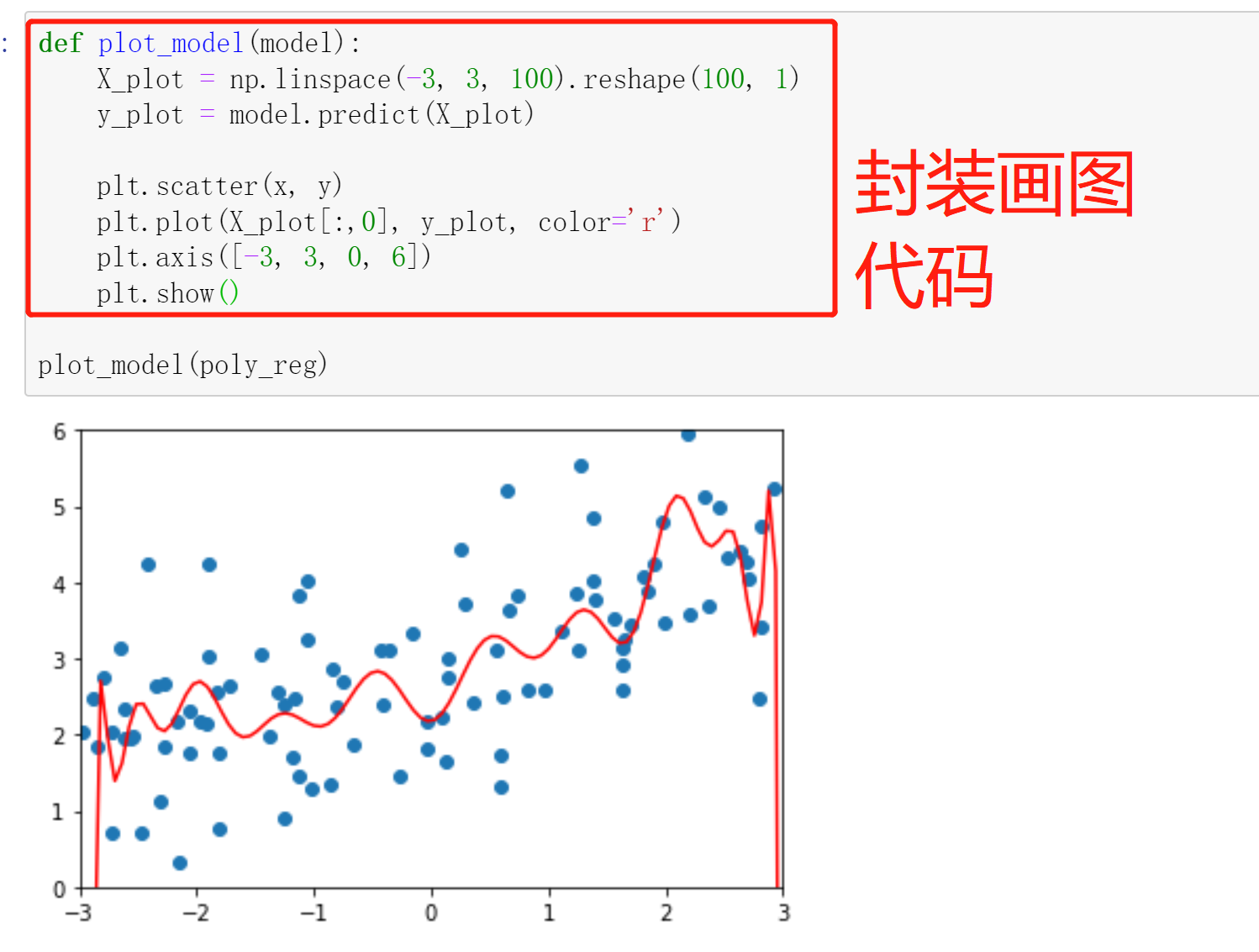
2.2.3 使用岭回归
from sklearn.linear_model import Ridgedef RidgeRegression(degree, alpha):return Pipeline([("poly", PolynomialFeatures(degree=degree)),("std_scaler", StandardScaler()),("ridge_reg", Ridge(alpha=alpha))])ridge1_reg = RidgeRegression(20, 0.0001)ridge1_reg.fit(X_train, y_train)y1_predict = ridge1_reg.predict(X_test)mean_squared_error(y_test, y1_predict) # 1.3233492754151852plot_model(ridge1_reg)
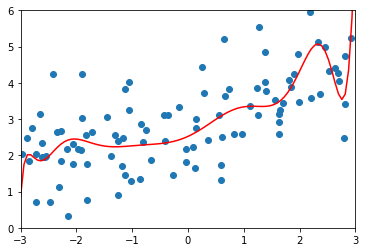
# 修改alpha值ridge2_reg = RidgeRegression(20, 1)ridge2_reg.fit(X_train, y_train)y2_predict = ridge2_reg.predict(X_test)mean_squared_error(y_test, y2_predict) # 1.1888759304218448plot_model(ridge2_reg)
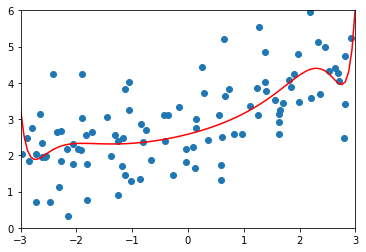
# 修改alpha值ridge3_reg = RidgeRegression(20, 100)ridge3_reg.fit(X_train, y_train)y3_predict = ridge3_reg.predict(X_test)mean_squared_error(y_test, y3_predict) # 1.31964561130862plot_model(ridge3_reg)
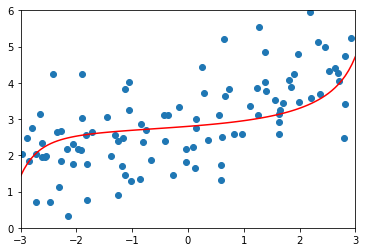
# 修改alpha值ridge4_reg = RidgeRegression(20, 10000000)ridge4_reg.fit(X_train, y_train)y4_predict = ridge4_reg.predict(X_test)mean_squared_error(y_test, y4_predict) # 1.8408455590998372plot_model(ridge4_reg)
3. LASSO回归
3.1 原理
Least Absolute Shrinkage and Selection Operator Regression
LASSO回归是模型正则化的一种方式。
目标:使 尽可能小。
3.2 编码
from sklearn.linear_model import Lassodef LassoRegression(degree, alpha):return Pipeline([("poly", PolynomialFeatures(degree=degree)),("std_scaler", StandardScaler()),("lasso_reg", Lasso(alpha=alpha))])lasso1_reg = LassoRegression(20, 0.01) # 这里的alpha是theta绝对值lasso1_reg.fit(X_train, y_train)y1_predict = lasso1_reg.predict(X_test)mean_squared_error(y_test, y1_predict) # 1.1496080843259968plot_model(lasso1_reg)
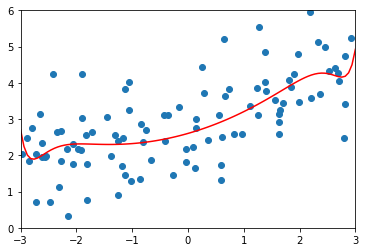
lasso2_reg = LassoRegression(20, 0.1)lasso2_reg.fit(X_train, y_train)y2_predict = lasso2_reg.predict(X_test)mean_squared_error(y_test, y2_predict) # 1.1213911351818648plot_model(lasso2_reg)
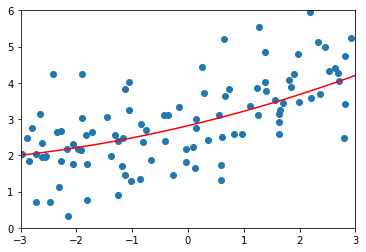
lasso3_reg = LassoRegression(20, 1)lasso3_reg.fit(X_train, y_train)y3_predict = lasso3_reg.predict(X_test)mean_squared_error(y_test, y3_predict) # 1.8408939659515595plot_model(lasso3_reg)
4.比较Ridge和LASOO
岭回归
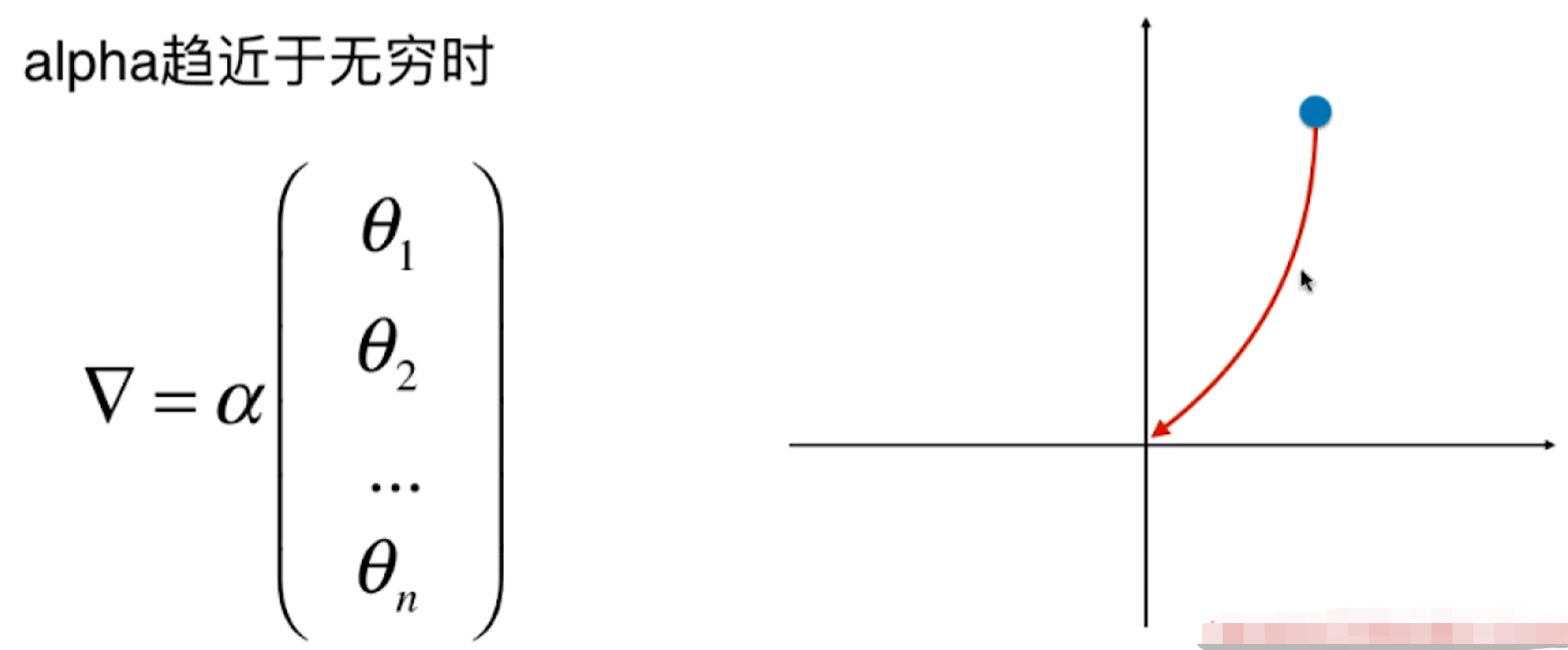
LASOO回归
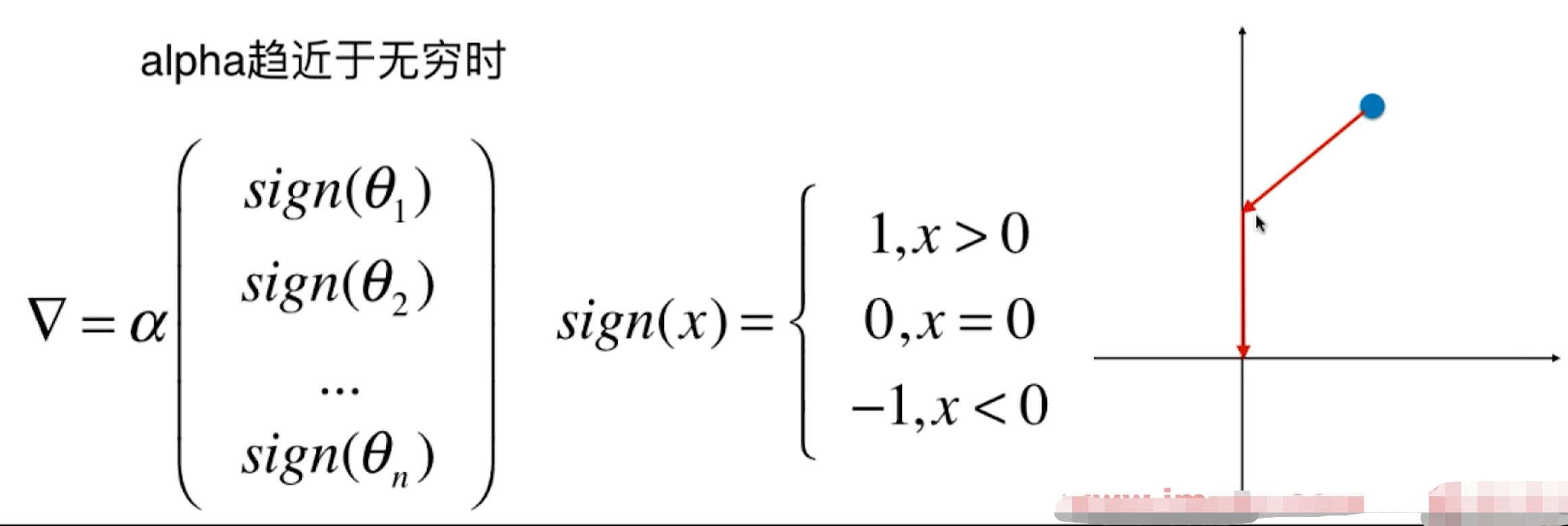
LASSO趋向于使得一部分theta值变为0。所以可作为特征选择用。
5.弹性网
6.总结
通常情况下,
1.先尝试岭回归
- 优点是计算是精准的
- 缺点是特征太大时,计算太大
2.其次尝试弹性网
因为弹性网结合了岭回归和LASSO回归的优点
3.LASSO回归
- 优点:速度快
- 缺点:急于将某些特征的参数华为0,造成偏差比较大