解释：同一个变量还有其它 项，叫做多项式。

线性回归

定义：从二维空间的角度看，说白了就是直线，从高维空间看，多变量看作一个向量，y值也是一条直线
优点：简单
缺点：不通用，现实生活中，一般不是线性关系

多项式回归

定义：从二维空间的角度看，说白了就是非线性
优点：通用，现实生活中，一般不是线性关系

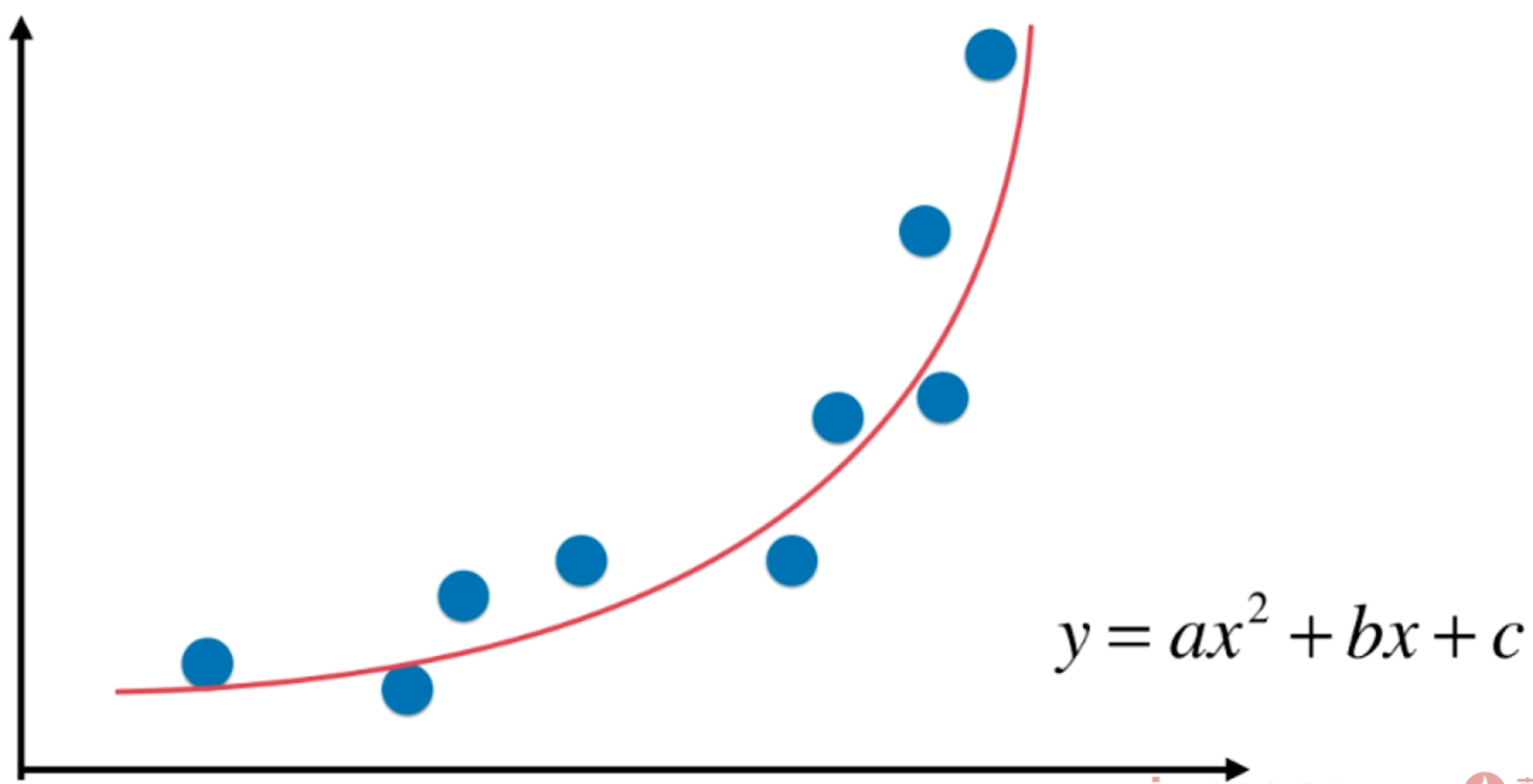
举例理解：
如下图，

• 理解成一个特征，理解成另一个特征， 依然是线性方程；
• 但是从 的角度看，是一个非线性的方程。

编码

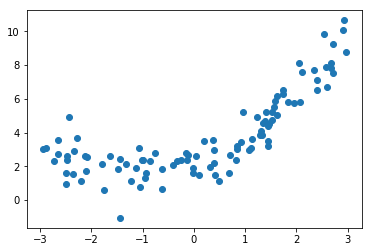
import numpy as np 
import matplotlib.pyplot as plt
# 准备数据
x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, 100)  # 加入正太分布噪音
# 可视化
plt.scatter(x, y)
plt.show()

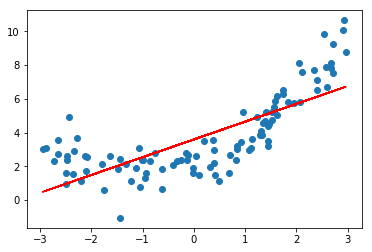
线性回归

from sklearn.linear_model import LinearRegression
# 建模
lin_reg = LinearRegression()
lin_reg.fit(X, y)
y_predict = lin_reg.predict(X)
# 模型可视化
plt.scatter(x, y)
plt.plot(x, y_predict, color='r')
plt.show()

多项式回归

解决方案：转换为多元线性回归问题 ( 添加一个特征 ：将另一个项作为一个特征)。
这里为了方便可视化，将另一个特征关联上第一个特征，公式里本质就是一个特征了。

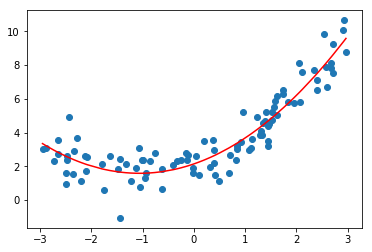
X2 = np.hstack([X, X**2])  # 两个特征: X、 X**2，这里的顺序和coef_顺序一致
X2.shape  # (100, 2)
lin_reg2 = LinearRegression()
lin_reg2.fit(X2, y)
# lin_reg.coef_  #     array([1.04523674, 0.49115908])  # 由于噪音数据的存在，只能接近系数 1 和 0.5
# lin_reg.intercept_  #  2.1464077470150507
y_predict2 = lin_reg2.predict(X2)
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict2[np.argsort(x)], color='r')  # 对x排序，画的曲线才是正常的
plt.show()