• 梯度上升法和 梯度下降法一样的，差别就是反向了，减法改为了加法。
  • 效用函数也叫目标函数。

    准备数据

    ```python import numpy as np import matplotlib.pyplot as plt

准备数据

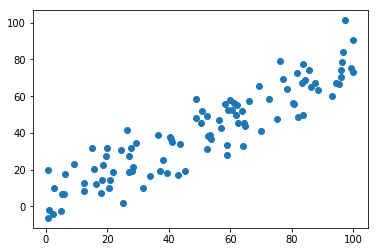
X = np.empty((100, 2)) X[:,0] = np.random.uniform(0., 100., size=100) # 第一列 X[:,1] = 0.75 * X[:,0] + 3. + np.random.normal(0, 10., size=100) # 第二列

plt.scatter(X[:,0], X[:,1]) plt.show()

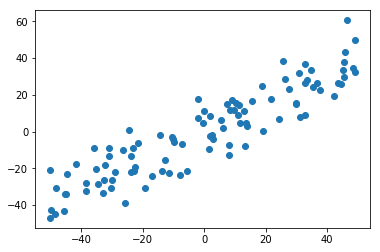
  1. ![image.png](https://cdn.nlark.com/yuque/0/2021/png/12405790/1637475078793-59806fbe-661d-4c98-9e0a-e9bd17a60016.png#clientId=uab742b7d-704e-4&from=paste&id=u193b04cf&margin=%5Bobject%20Object%5D&name=image.png&originHeight=252&originWidth=378&originalType=url&ratio=1&size=7133&status=done&style=none&taskId=ub070a52f-8b85-408f-afa7-4629df6650d)
  2. <a name="RgYlw"></a>
  3. # 数据预处理
  4. <a name="IL1xD"></a>
  5. ## demean
  6. 均值归零：把样本点移动到坐标系原点附近。
  7. ```python
  8. def demean(X):
  9.     return X - np.mean(X, axis=0)
  11. X_demean = demean(X)
  12. plt.scatter(X_demean[:,0], X_demean[:,1])
  13. plt.show()

image.png

  1. # 检查预处理结果：两列均值均接近0
  2. np.mean(X_demean[:,0])  # 8.171241461241152e-15
  3. np.mean(X_demean[:,1])  # -1.0231815394945442e-14

模型封装

  1. def f(w, X):
  2.     '''目标函数'''
  3.     return np.sum((X.dot(w)**2)) / len(X)
  5. def df_math(w, X):
  6.     '''目标函数的梯度: 矩阵实现'''
  7.     return X.T.dot(X.dot(w)) * 2. / len(X)
  9. def df_debug(w, X, epsilon=0.0001):
  10.     '''目标函数的梯度：迭代实现'''
  11.     res = np.empty(len(w))
  12.     for i in range(len(w)):
  13.         w_1 = w.copy()
  14.         w_1[i] += epsilon
  15.         w_2 = w.copy()
  16.         w_2[i] -= epsilon
  17.         res[i] = (f(w_1, X) - f(w_2, X)) / (2 * epsilon)
  18.     return res
  20. def direction(w):
  21.     '''w的单位向量'''
  22.     return w / np.linalg.norm(w)
  24. def gradient_ascent(df, X, initial_w, eta, n_iters = 1e4, epsilon=1e-8):
  25.      '''目标函数的梯度上升法'''
  26.     w = direction(initial_w) 
  27.     cur_iter = 0
  29.     while cur_iter < n_iters:
  30.         gradient = df(w, X)
  31.         last_w = w
  32.         w = w + eta * gradient
  33.         w = direction(w) # 注意1：每次求一个单位方向
  34.         if(abs(f(w, X) - f(last_w, X)) < epsilon):
  35.             break
  37.         cur_iter += 1
  39.     return w

编码实现

  1. # 建模
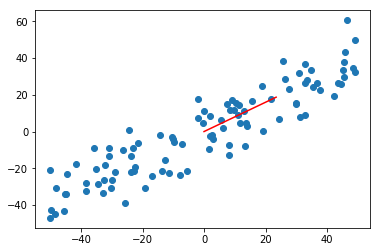
  2. initial_w = np.random.random(X.shape[1]) # 注意2：不能用0向量开始
  3. initial_w  # array([0.19082376, 0.43894239])
  5. eta = 0.001
  6. ## 注意3： 不能使用StandardScaler标准化数据
  8. w = gradient_ascent(df_debug, X_demean, initial_w, eta)  # array([0.78159851, 0.62378183])
  9. w = gradient_ascent(df_debug, X_demean, initial_w, eta)  # array([0.78159851, 0.62378183])
  11. # 可视化
  12. plt.scatter(X_demean[:,0], X_demean[:,1])
  13. plt.plot([0, w[0]*30], [0, w[1]*30], color='r')
  14. plt.show()

image.png
解释：红线（向量w）就是样本点数据方差最大的向量。

极端数据集测试

准备数据

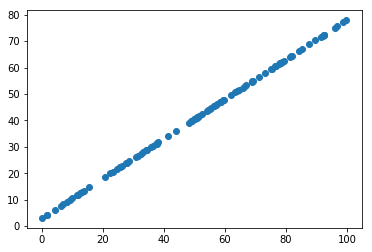
  1. X2 = np.empty((100, 2))
  2. X2[:,0] = np.random.uniform(0., 100., size=100)
  3. X2[:,1] = 0.75 * X2[:,0] + 3.
  5. plt.scatter(X2[:,0], X2[:,1])
  6. plt.show()

image.png

预处理

  1. X2_demean = demean(X2)
  2. np.mean(X_demean[:,0])  # 8.171241461241152e-15
  3. np.mean(X_demean[:,1])  # -1.0231815394945442e-14

建模

  1. w2 = gradient_ascent(df_math, X2_demean, initial_w, eta)

可视化

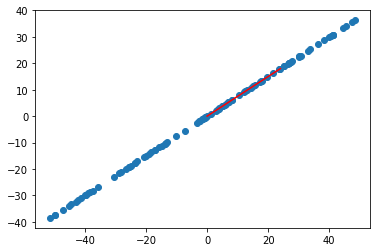
  1. plt.scatter(X2_demean[:,0], X2_demean[:,1])  # 样本点
  2. plt.plot([0, w2[0]*30], [0, w2[1]*30], color='r')  # PCA向量
  3. plt.show()

image.png
和梯度下降法一样，梯度上升法 也有随机梯度和小批量梯度。