第二主成分

求出第一主成分以后，如何求出下一个主成分?

• 数据进行改变，将数据在第一个主成分上的分量去掉
• 在新的数据上求第一主成分(即对 求第一主成分)

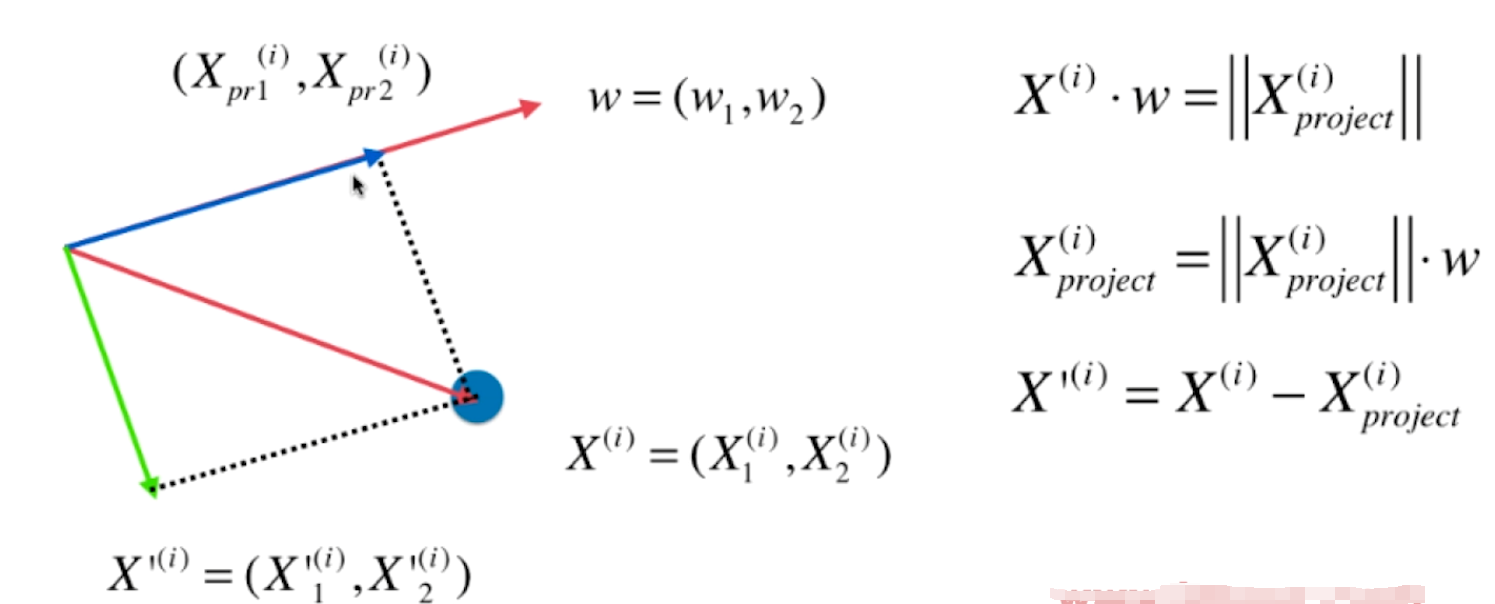
准备数据

import numpy as np
import matplotlib.pyplot as plt
X = np.empty((100, 2))
X[:,0] = np.random.uniform(0., 100., size=100)
X[:,1] = 0.75 * X[:,0] + 3. + np.random.normal(0, 10., size=100)
# 去中心化
def demean(X):
    return X - np.mean(X, axis=0)
X = demean(X)
# 可视化
plt.scatter(X[:,0], X[:,1])
plt.show()

封装模型

# 效用函数
def f(w, X):
    return np.sum((X.dot(w)**2)) / len(X)
# 梯度
def df(w, X):
    return X.T.dot(X.dot(w)) * 2. / len(X)
# 方向
def direction(w):
    return w / np.linalg.norm(w)
# 求第一主成分
def first_component(X, initial_w, eta, n_iters = 1e4, epsilon=1e-8):
    w = direction(initial_w) 
    cur_iter = 0
    while cur_iter < n_iters:
        gradient = df(w, X)
        last_w = w
        w = w + eta * gradient
        w = direction(w) 
        if(abs(f(w, X) - f(last_w, X)) < epsilon):
            break
        cur_iter += 1
    return w

求第一主成分

主成分是个向量

initial_w = np.random.random(X.shape[1])
eta = 0.01
w = first_component(X, initial_w, eta)  # array([0.7692998 , 0.63888796])

求第二主成分

X2 = np.empty(X.shape)
for i in range(len(X)):
    X2[i] = X[i] - X[i].dot(w) * w
plt.scatter(X2[:,0], X2[:,1])
plt.show()

w2 = first_component(X2, initial_w, eta)  # array([ 0.63889083, -0.76929741])  # 第二主成分

验证

w.dot(w2)  # 3.733763445973939e-06 第一主成分 * 第二主成分 = 0，说明两个轴垂直

求前N个主成分

一次求一个主成分太麻烦了，再封装下。

封装模型

def first_n_components(n, X, eta=0.01, n_iters = 1e4, epsilon=1e-8):
    X_pca = X.copy()
    X_pca = demean(X_pca)
    res = []
    for i in range(n):
        initial_w = np.random.random(X_pca.shape[1])
        w = first_component(X_pca, initial_w, eta)
        res.append(w)
        X_pca = X_pca - X_pca.dot(w).reshape(-1, 1) * w
    return res

求解

first_n_components(2, X)  # [array([0.76929985, 0.63888789]), array([ 0.63889151, -0.76929685])]