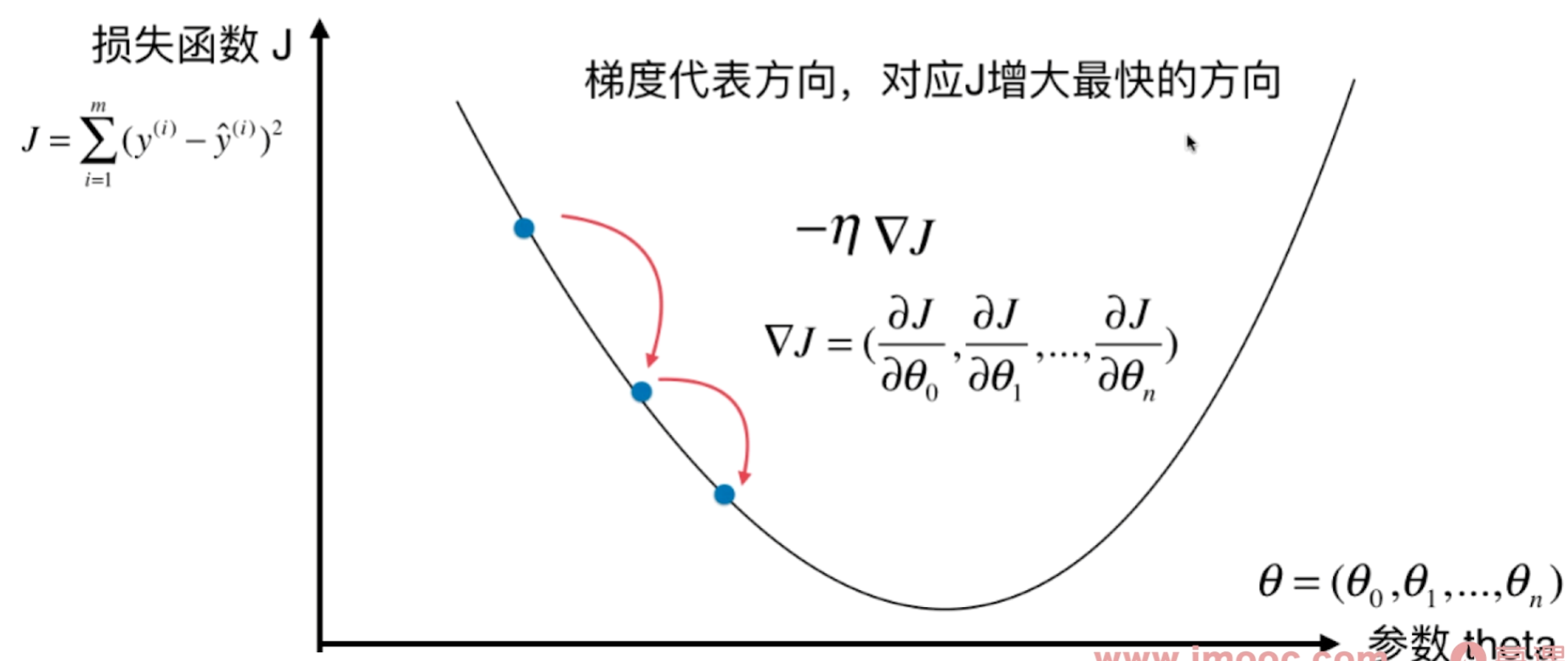
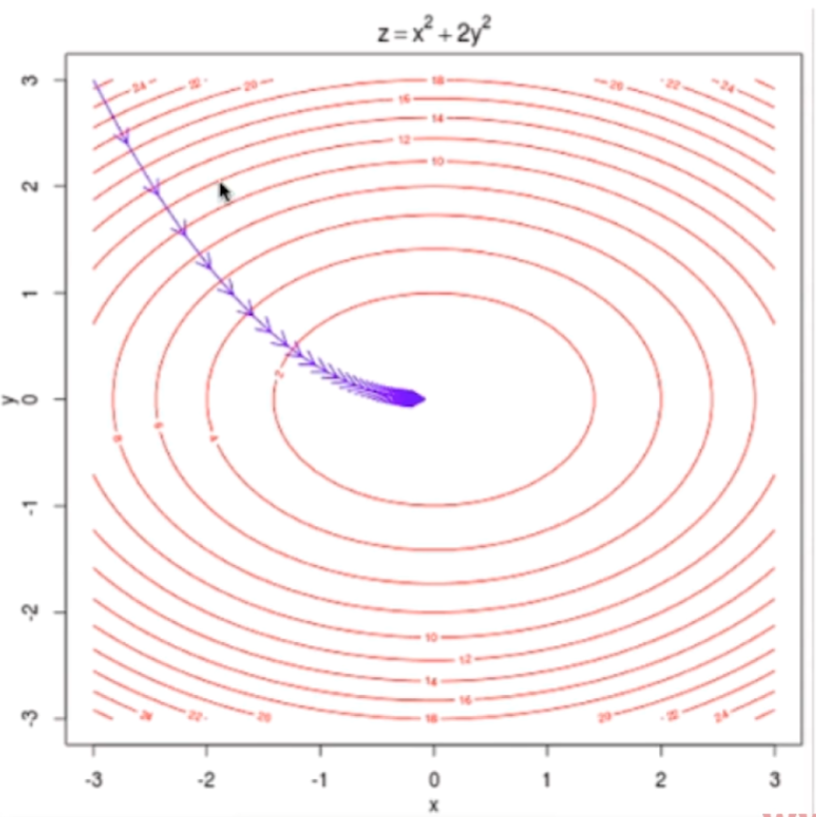
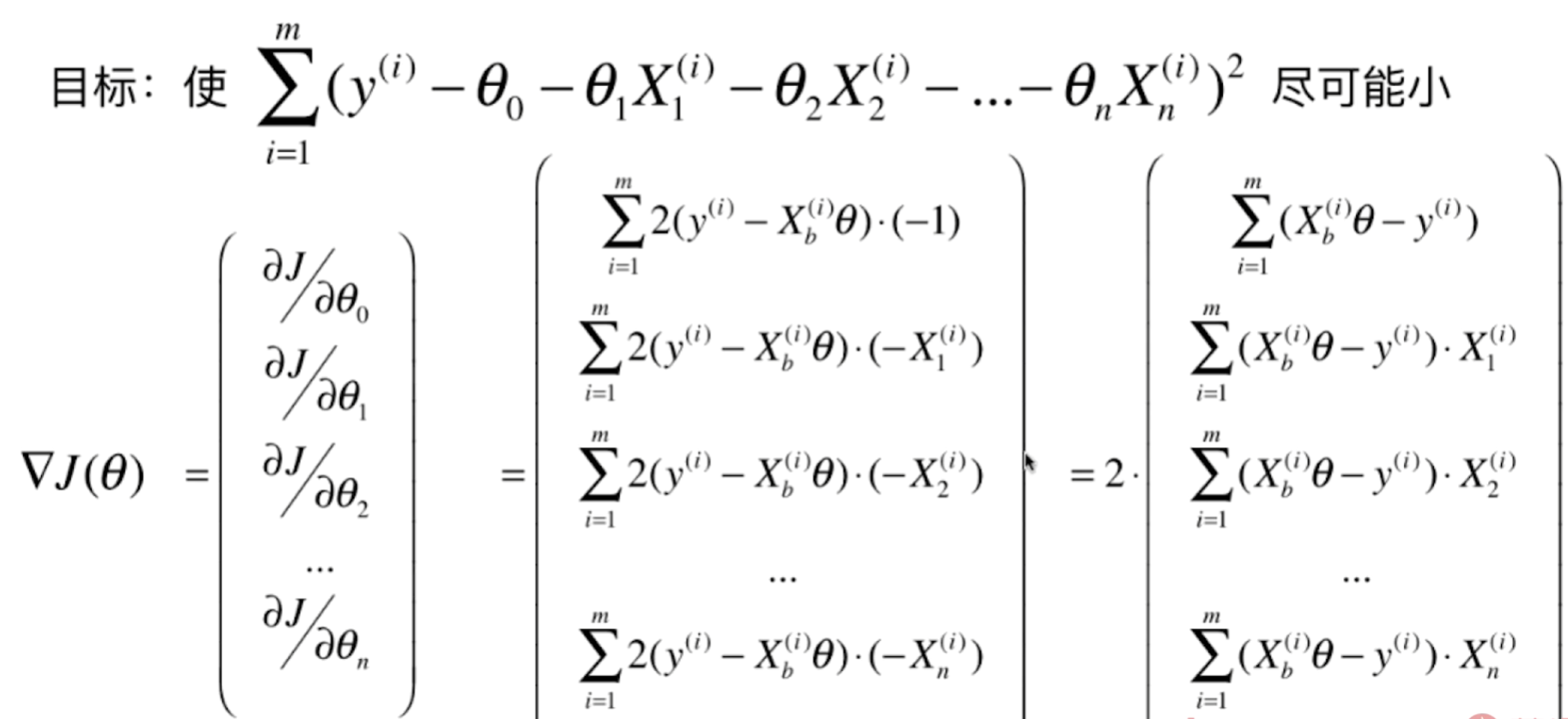多元回归损失函数

image.png

二元回归图解

image.png

损失函数公式推导

image.png
此时，损失函数和 m 有关，因此需要 除以m 。
image.png

编码实现

准备数据

  1. import numpy as np
  2. import matplotlib.pyplot as plt
  4. np.random.seed(666)
  5. x = 2 * np.random.random(size=100)
  6. y = x * 3. + 4. + np.random.normal(size=100)
  7. x
  1. array([1.40087424, 1.68837329, 1.35302867, 1.45571611, 1.90291591,
  2.        0.02540639, 0.8271754 , 0.09762559, 0.19985712, 1.01613261,
  3.        0.40049508, 1.48830834, 0.38578401, 1.4016895 , 0.58645621,
  4.        1.54895891, 0.01021768, 0.22571531, 0.22190734, 0.49533646,
  5.        0.0464726 , 1.45464231, 0.68006988, 0.39500631, 1.81835919,
  6.        1.95669397, 1.06560509, 0.5182637 , 1.16762524, 0.65138131,
  7.        1.77779863, 1.25280905, 1.63774738, 1.09469084, 0.83342401,
  8.        1.48609438, 0.73919276, 0.15033309, 1.55038596, 0.43881849,
  9.        0.15868425, 0.97356104, 0.3073478 , 1.65693027, 0.38273714,
  10.        0.54081791, 1.12206884, 1.80476078, 1.70357668, 0.83616392,
  11.        0.78695254, 0.03244103, 0.59842674, 0.70755644, 1.78700533,
  12.        1.57227314, 1.54277385, 0.84010971, 1.55205028, 0.92861629,
  13.        0.36354033, 1.76805121, 1.43758454, 1.3437626 , 0.51312727,
  14.        0.86160364, 0.03290715, 0.46998765, 1.02234262, 0.58401848,
  15.        1.00378702, 0.99654626, 0.20754305, 0.89288623, 1.93837834,
  16.        1.47694224, 1.43910122, 1.78608677, 1.92534936, 0.39410046,
  17.        1.42917993, 0.32384788, 1.73250954, 1.24764049, 1.91891025,
  18.        1.04828408, 0.07286576, 1.45374316, 0.00781969, 0.100588  ,
  19.        1.98398463, 0.424515  , 1.89474133, 0.9030811 , 1.99758935,
  20.        1.29500298, 1.40448142, 0.85916353, 0.33554952, 0.23626619])
  1. X = x.reshape(-1, 1)  # 转二维，方便处理多维数据
  2. X[:20]
  1. array([[1.40087424],
  2.        [1.68837329],
  3.        [1.35302867],
  4.        [1.45571611],
  5.        [1.90291591],
  6.        [0.02540639],
  7.        [0.8271754 ],
  8.        [0.09762559],
  9.        [0.19985712],
  10.        [1.01613261],
  11.        [0.40049508],
  12.        [1.48830834],
  13.        [0.38578401],
  14.        [1.4016895 ],
  15.        [0.58645621],
  16.        [1.54895891],
  17.        [0.01021768],
  18.        [0.22571531],
  19.        [0.22190734],
  20.        [0.49533646]])
  1. y[:20]
  1. array([8.91412688, 8.89446981, 8.85921604, 9.04490343, 8.75831915,
  2.        4.01914255, 6.84103696, 4.81582242, 3.68561238, 6.46344854,
  3.        4.61756153, 8.45774339, 3.21438541, 7.98486624, 4.18885101,
  4.        8.46060979, 4.29706975, 4.06803046, 3.58490782, 7.0558176 ])
  1. plt.scatter(x, y)
  2. plt.show()

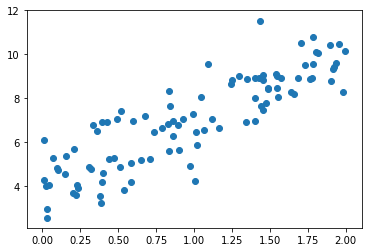
image.png

使用梯度下降法训练

  1. def J(theta, X_b, y):
  2.     try:
  3.         return np.sum((y - X_b.dot(theta))**2) / len(X_b)
  4.     except:
  5.         return float('inf')
  1. def dJ(theta, X_b, y):
  2.     res = np.empty(len(theta))
  3.     res[0] = np.sum(X_b.dot(theta) - y)
  4.     for i in range(1, len(theta)):
  5.         res[i] = (X_b.dot(theta) - y).dot(X_b[:,i])
  6.     return res * 2 / len(X_b)
  1. def gradient_descent(X_b, y, initial_theta, eta, n_iters = 1e4, epsilon=1e-8):
  3.     theta = initial_theta
  4.     cur_iter = 0
  6.     while cur_iter < n_iters:
  7.         gradient = dJ(theta, X_b, y)
  8.         last_theta = theta
  9.         theta = theta - eta * gradient
  10.         if(abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
  11.             break
  13.         cur_iter += 1
  15.     return theta
  1. X_b = np.hstack([np.ones((len(x), 1)), x.reshape(-1,1)])
  2. initial_theta = np.zeros(X_b.shape[1])
  3. eta = 0.01
  5. theta = gradient_descent(X_b, y, initial_theta, eta)
  6. theta  # array([4.02145786, 3.00706277])

封装模型

  1. # LinearRegression.py
  2. import numpy as np
  3. from .metrics import r2_score
  5. class LinearRegression:
  7.     def __init__(self):
  8.         """初始化Linear Regression模型"""
  9.         self.coef_ = None
  10.         self.intercept_ = None
  11.         self._theta = None
  13.     def fit_normal(self, X_train, y_train):
  14.         """根据训练数据集X_train, y_train训练Linear Regression模型"""
  15.         assert X_train.shape[0] == y_train.shape[0], \
  16.             "the size of X_train must be equal to the size of y_train"
  18.         X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
  19.         self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)
  21.         self.intercept_ = self._theta[0]
  22.         self.coef_ = self._theta[1:]
  24.         return self
  26.     def fit_gd(self, X_train, y_train, eta=0.01, n_iters=1e4):
  27.         """根据训练数据集X_train, y_train, 使用梯度下降法训练Linear Regression模型"""
  28.         assert X_train.shape[0] == y_train.shape[0], \
  29.             "the size of X_train must be equal to the size of y_train"
  31.         def J(theta, X_b, y):
  32.             try:
  33.                 return np.sum((y - X_b.dot(theta)) ** 2) / len(y)
  34.             except:
  35.                 return float('inf')
  37.         def dJ(theta, X_b, y):
  38.             res = np.empty(len(theta))
  39.             res[0] = np.sum(X_b.dot(theta) - y)
  40.             for i in range(1, len(theta)):
  41.                 res[i] = (X_b.dot(theta) - y).dot(X_b[:, i])
  42.             return res * 2 / len(X_b)
  44.         def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):
  46.             theta = initial_theta
  47.             cur_iter = 0
  49.             while cur_iter < n_iters:
  50.                 gradient = dJ(theta, X_b, y)
  51.                 last_theta = theta
  52.                 theta = theta - eta * gradient
  53.                 if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
  54.                     break
  56.                 cur_iter += 1
  58.             return theta
  60.         X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
  61.         initial_theta = np.zeros(X_b.shape[1])
  62.         self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)
  64.         self.intercept_ = self._theta[0]
  65.         self.coef_ = self._theta[1:]
  67.         return self
  69.     def predict(self, X_predict):
  70.         """给定待预测数据集X_predict，返回表示X_predict的结果向量"""
  71.         assert self.intercept_ is not None and self.coef_ is not None, \
  72.             "must fit before predict!"
  73.         assert X_predict.shape[1] == len(self.coef_), \
  74.             "the feature number of X_predict must be equal to X_train"
  76.         X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
  77.         return X_b.dot(self._theta)
  79.     def score(self, X_test, y_test):
  80.         """根据测试数据集 X_test 和 y_test 确定当前模型的准确度"""
  82.         y_predict = self.predict(X_test)
  83.         return r2_score(y_test, y_predict)
  85.     def __repr__(self):
  86.         return "LinearRegression()"

编码实现

  1. import numpy as np
  2. import matplotlib.pyplot as plt
  5. # 准备数据
  6. np.random.seed(666)
  7. x = 2 * np.random.random(size=100)
  8. y = x * 3. + 4. + np.random.normal(size=100)
  9. X = x.reshape(-1, 1)  # 为了将数据转换为一列
  11. from playML.LinearRegression import LinearRegression
  12. lin_reg = LinearRegression()
  13. lin_reg.fit_gd(X, y)
  14. lin_reg.coef_ # array([ 3.00706277])
  15. lin_reg.intercept_  # 4.021457858204859

模型优化

提升性能：向量化代替for循环（计算机的算法优化）

  1. import numpy as np
  2. from sklearn import datasets
  4. # 准备数据
  5. boston = datasets.load_boston()
  6. X = boston.data
  7. y = boston.target
  9. X = X[y < 50.0]
  10. y = y[y < 50.0]
  12. from playML.model_selection import train_test_split
  13. X_train, X_test, y_train, y_test = train_test_split(X, y, seed=666)
  15. # 线性回归
  16. from playML.LinearRegression import LinearRegression
  17. lin_reg1 = LinearRegression()
  18. %time lin_reg1.fit_normal(X_train, y_train)  # Wall time: 997 µs
  19. lin_reg1.score(X_test, y_test)  # 0.812980260265854

使用梯度下降法

使用梯度下降法前进行数据归一化

  1. from sklearn.preprocessing import StandardScaler
  3. standardScaler = StandardScaler()
  4. standardScaler.fit(X_train)
  5. X_train_standard = standardScaler.transform(X_train)
  7. lin_reg3 = LinearRegression() 
  8. %time lin_reg3.fit_gd(X_train_standard, y_train)  # Wall time: 123 ms
  10. X_test_standard = standardScaler.transform(X_test)
  11. lin_reg3.score(X_test_standard, y_test)  # 0.8129880620122235

梯度下降法的优势

  1. m = 1000
  2. n = 5000
  4. big_X = np.random.normal(size=(m, n))
  5. true_theta = np.random.uniform(0.0, 100.0, size=n+1)
  6. big_y = big_X.dot(true_theta[1:]) + true_theta[0] + np.random.normal(0., 10., size=m)
  8. big_reg1 = LinearRegression()  # Wall time: 3.88 s
  9. %time big_reg1.fit_normal(big_X, big_y) 
  11. big_reg2 = LinearRegression()
  12. %time big_reg2.fit_gd(big_X, big_y)  # Wall time: 3.72 s

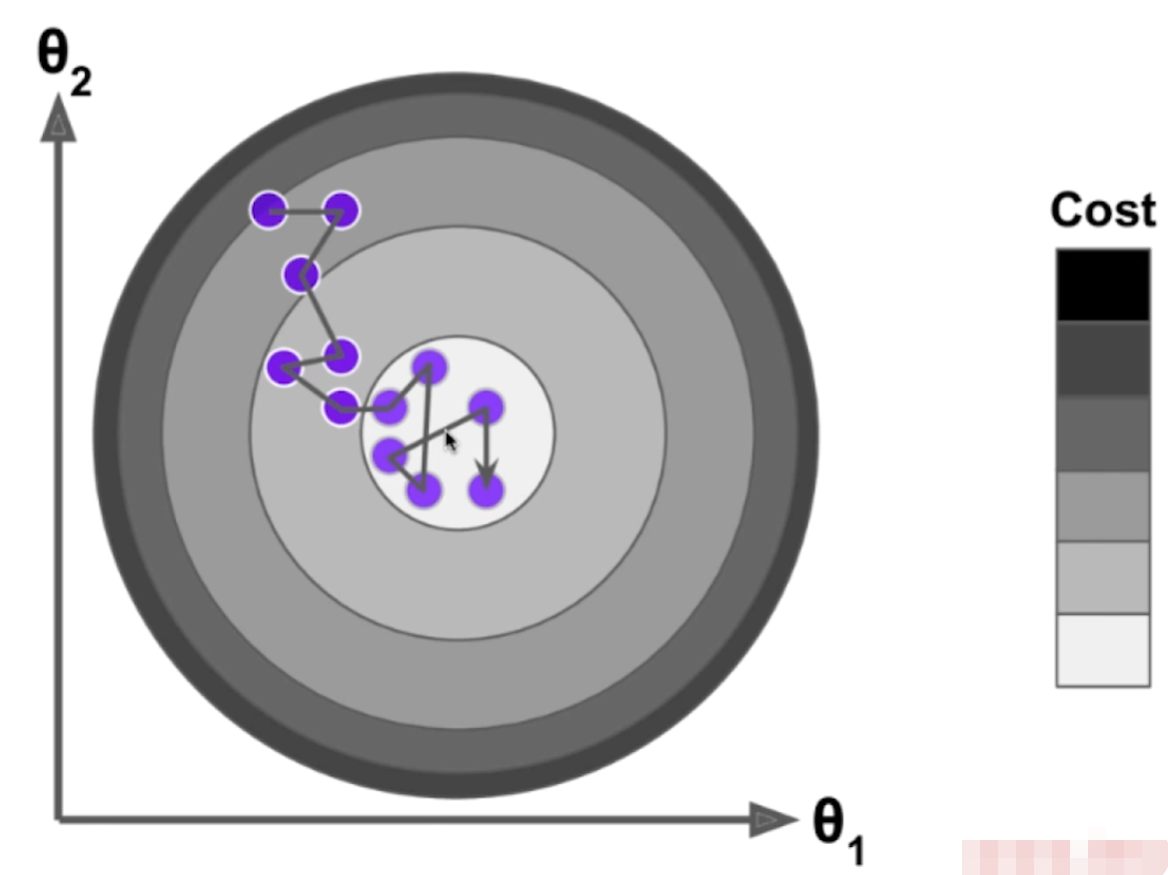
随机梯度下降法

优点：比原始梯度下降速度更快，但是没有那么精确。

模拟实现

image.png

  1. import numpy as np
  2. import matplotlib.pyplot as plt
  4. # 准备数据
  5. m = 100000
  6. x = np.random.normal(size=m)
  7. X = x.reshape(-1,1)
  8. y = 4.*x + 3. + np.random.normal(0, 3, size=m)
  10. plt.scatter(x, y)
  11. plt.show()

image.png

  1. def J(theta, X_b, y):
  2.     try:
  3.         return np.sum((y - X_b.dot(theta)) ** 2) / len(y)
  4.     except:
  5.         return float('inf')
  7. def dJ(theta, X_b, y):
  8.     return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(y)
  10. def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):
  12.     theta = initial_theta
  13.     cur_iter = 0
  15.     while cur_iter < n_iters:
  16.         gradient = dJ(theta, X_b, y)
  17.         last_theta = theta
  18.         theta = theta - eta * gradient
  19.         if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
  20.             break
  22.         cur_iter += 1
  24.     return theta
  27. %%time  # Wall time: 884 ms
  28. X_b = np.hstack([np.ones((len(X), 1)), X])
  29. initial_theta = np.zeros(X_b.shape[1])
  30. eta = 0.01
  31. theta = gradient_descent(X_b, y, initial_theta, eta)  # array([3.00317559, 4.01432714])
  1. def dJ_sgd(theta, X_b_i, y_i):
  2.     return 2 * X_b_i.T.dot(X_b_i.dot(theta) - y_i)
  4. def sgd(X_b, y, initial_theta, n_iters):
  6.     t0, t1 = 5, 50
  7.     def learning_rate(t):
  8.         return t0 / (t + t1)
  10.     theta = initial_theta
  11.     for cur_iter in range(n_iters):    
  12.         rand_i = np.random.randint(len(X_b))
  13.         gradient = dJ_sgd(theta, X_b[rand_i], y[rand_i])
  14.         theta = theta - learning_rate(cur_iter) * gradient
  16.     return theta
  18. %%time  # Wall time: 226 ms
  19. X_b = np.hstack([np.ones((len(X), 1)), X])
  20. initial_theta = np.zeros(X_b.shape[1])
  21. theta = sgd(X_b, y, initial_theta, n_iters=m//3)
  22. theta  # array([ 3.04732375,  4.03214249])

封装SGD模型

  1. import numpy as np
  2. from .metrics import r2_score
  4. class LinearRegression:
  6.     def __init__(self):
  7.         """初始化Linear Regression模型"""
  8.         self.coef_ = None
  9.         self.intercept_ = None
  10.         self._theta = None
  12.     def fit_normal(self, X_train, y_train):
  13.         """根据训练数据集X_train, y_train训练Linear Regression模型"""
  14.         assert X_train.shape[0] == y_train.shape[0], \
  15.             "the size of X_train must be equal to the size of y_train"
  17.         X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
  18.         self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)
  20.         self.intercept_ = self._theta[0]
  21.         self.coef_ = self._theta[1:]
  23.         return self
  25.     def fit_bgd(self, X_train, y_train, eta=0.01, n_iters=1e4):
  26.         """根据训练数据集X_train, y_train, 使用梯度下降法训练Linear Regression模型"""
  27.         assert X_train.shape[0] == y_train.shape[0], \
  28.             "the size of X_train must be equal to the size of y_train"
  30.         def J(theta, X_b, y):
  31.             try:
  32.                 return np.sum((y - X_b.dot(theta)) ** 2) / len(y)
  33.             except:
  34.                 return float('inf')
  36.         def dJ(theta, X_b, y):
  37.             return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(y)
  39.         def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):
  41.             theta = initial_theta
  42.             cur_iter = 0
  44.             while cur_iter < n_iters:
  45.                 gradient = dJ(theta, X_b, y)
  46.                 last_theta = theta
  47.                 theta = theta - eta * gradient
  48.                 if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
  49.                     break
  51.                 cur_iter += 1
  53.             return theta
  55.         X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
  56.         initial_theta = np.zeros(X_b.shape[1])
  57.         self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)
  59.         self.intercept_ = self._theta[0]
  60.         self.coef_ = self._theta[1:]
  62.         return self
  64.     def fit_sgd(self, X_train, y_train, n_iters=50, t0=5, t1=50):
  65.         """根据训练数据集X_train, y_train, 使用梯度下降法训练Linear Regression模型"""
  66.         assert X_train.shape[0] == y_train.shape[0], \
  67.             "the size of X_train must be equal to the size of y_train"
  68.         assert n_iters >= 1
  70.         def dJ_sgd(theta, X_b_i, y_i):
  71.             return X_b_i * (X_b_i.dot(theta) - y_i) * 2.
  73.         def sgd(X_b, y, initial_theta, n_iters=5, t0=5, t1=50):
  75.             def learning_rate(t):
  76.                 return t0 / (t + t1)
  78.             theta = initial_theta
  79.             m = len(X_b)
  80.             for i_iter in range(n_iters):
  81.                 indexes = np.random.permutation(m)
  82.                 X_b_new = X_b[indexes,:]
  83.                 y_new = y[indexes]
  84.                 for i in range(m):
  85.                     gradient = dJ_sgd(theta, X_b_new[i], y_new[i])
  86.                     theta = theta - learning_rate(i_iter * m + i) * gradient
  88.             return theta
  90.         X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
  91.         initial_theta = np.random.randn(X_b.shape[1])
  92.         self._theta = sgd(X_b, y_train, initial_theta, n_iters, t0, t1)
  94.         self.intercept_ = self._theta[0]
  95.         self.coef_ = self._theta[1:]
  97.         return self
  99.     def predict(self, X_predict):
  100.         """给定待预测数据集X_predict，返回表示X_predict的结果向量"""
  101.         assert self.intercept_ is not None and self.coef_ is not None, \
  102.             "must fit before predict!"
  103.         assert X_predict.shape[1] == len(self.coef_), \
  104.             "the feature number of X_predict must be equal to X_train"
  106.         X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
  107.         return X_b.dot(self._theta)
  109.     def score(self, X_test, y_test):
  110.         """根据测试数据集 X_test 和 y_test 确定当前模型的准确度"""
  112.         y_predict = self.predict(X_test)
  113.         return r2_score(y_test, y_predict)
  115.     def __repr__(self):
  116.         return "LinearRegression()"

模拟实现封装的SGD模型

模拟数据

  1. import numpy as np
  2. import matplotlib.pyplot as plt
  4. m = 100000
  5. x = np.random.normal(size=m)
  6. X = x.reshape(-1,1)
  7. y = 4.*x + 3. + np.random.normal(0, 3, size=m)
  9. from playML.LinearRegression import LinearRegression
  10. lin_reg = LinearRegression()
  11. lin_reg.fit_bgd(X, y)
  12. print(lin_reg.intercept_, lin_reg.coef_)  # 3.01644183437 [ 3.99995653]
  14. lin_reg = LinearRegression()
  15. lin_reg.fit_sgd(X, y, n_iters=2)
  16. print(lin_reg.intercept_, lin_reg.coef_)  # 2.99558568395 [ 4.02610767]

数据归一化

梯度下降是一种搜索算法，过程中涉及各个特征，这就导致了每次的梯度值的大小受各个特征数值规模的影响，因此把数据归一化可以达到大大减小每次梯度值的效果，从而加速梯度下降。

真实实现封装的SGD模型

真实数据

  1. from sklearn import datasets
  3. # 准备数据
  4. boston = datasets.load_boston()
  5. X = boston.data
  6. y = boston.target
  8. X = X[y < 50.0]
  9. y = y[y < 50.0]
  11. # 数据预处理
  12. ## 数据分割：训练集、测试集
  13. from playML.model_selection import train_test_split
  14. X_train, X_test, y_train, y_test = train_test_split(X, y, seed=666)
  17. ## 数据归一化
  18. from sklearn.preprocessing import StandardScaler
  19. standardScaler = StandardScaler()
  20. standardScaler.fit(X_train)
  21. X_train_standard = standardScaler.transform(X_train)
  22. X_test_standard = standardScaler.transform(X_test)
  24. # 建模
  25. from playML.LinearRegression import LinearRegression
  26. lin_reg = LinearRegression()
  27. %time lin_reg.fit_sgd(X_train_standard, y_train, n_iters=2)  # Wall time: 3.99 ms
  28. lin_reg.score(X_test_standard, y_test)  # 0.78651716204682975
  30. ## 调整n_iters
  31. %time lin_reg.fit_sgd(X_train_standard, y_train, n_iters=50)  # Wall time: 78.8 ms
  32. lin_reg.score(X_test_standard, y_test)  # 0.8085728716573835
  34. %time lin_reg.fit_sgd(X_train_standard, y_train, n_iters=100)  # Wall time: 157 ms
  35. lin_reg.score(X_test_standard, y_test)  # 0.8129484613272351

scikit-learn中的SGD

  1. from sklearn.linear_model import SGDRegressor
  3. sgd_reg = SGDRegressor()
  4. %time sgd_reg.fit(X_train_standard, y_train)  # Wall time: 185 ms
  5. sgd_reg.score(X_test_standard, y_test)  # 0.8047845970157302
  7. sgd_reg = SGDRegressor(n_iter=50)
  8. %time sgd_reg.fit(X_train_standard, y_train)  # Wall time: 1.99 ms
  9. sgd_reg.score(X_test_standard, y_test)  # 0.8119907393187841