多元：有多个自变量 x1 、 x2 、x3 …
解释：一个因素受到多个因素的影响的规律，X(x1,x2,x3…)可看作一个向量，y值呈显现规律。
公式：

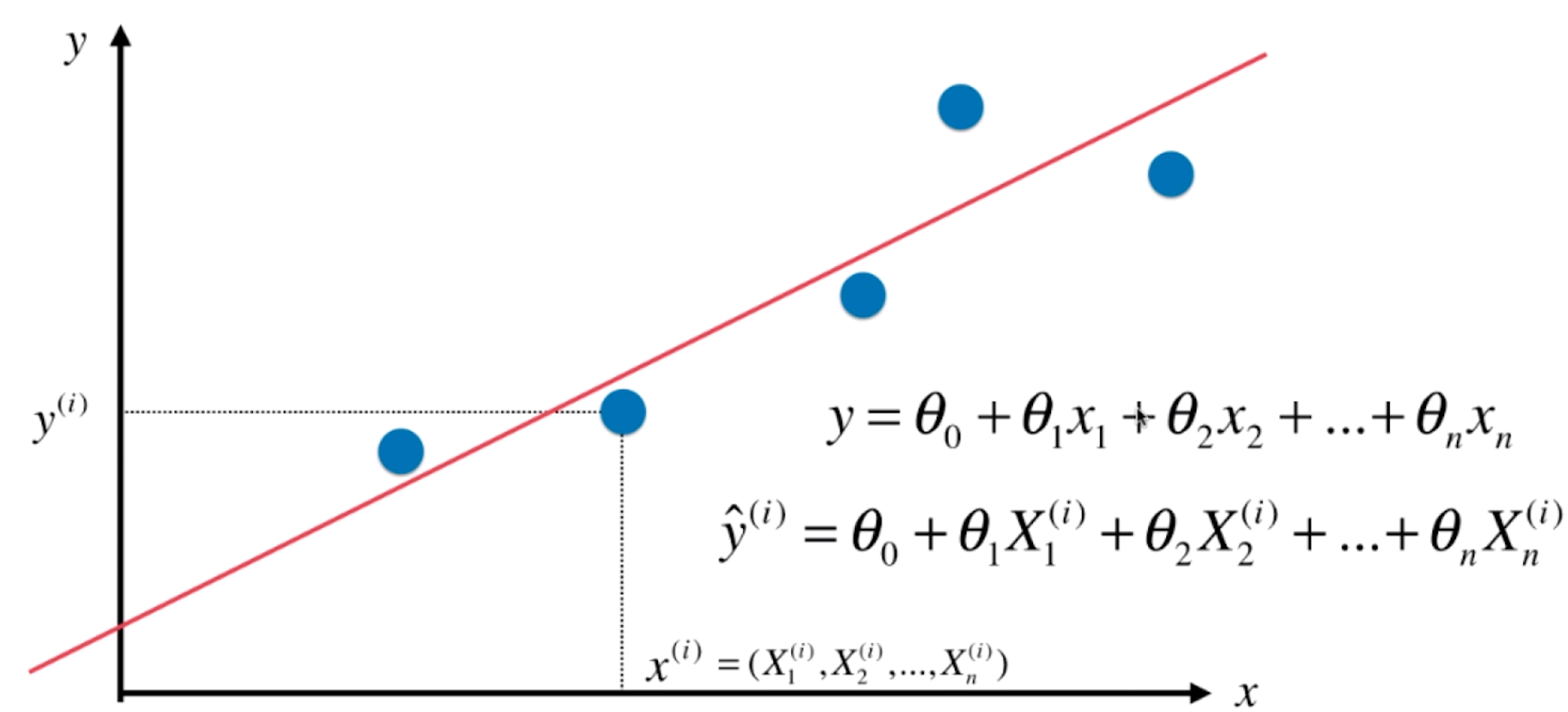
0.一元线性回归理解多元线性回归

其中第二个就是理论回归方程。因为多元线性回归一个观测值就不再是一个标量而是一个向量了，所以可能自变量的观测值就变成了 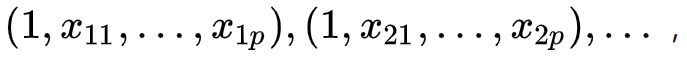而对应的因变量的观测值不变，还是 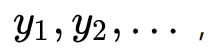因此我们把这些观测值每一行每一行的叠加起来就成为了一个向量或者矩阵，所以引入矩阵的表示是必要的。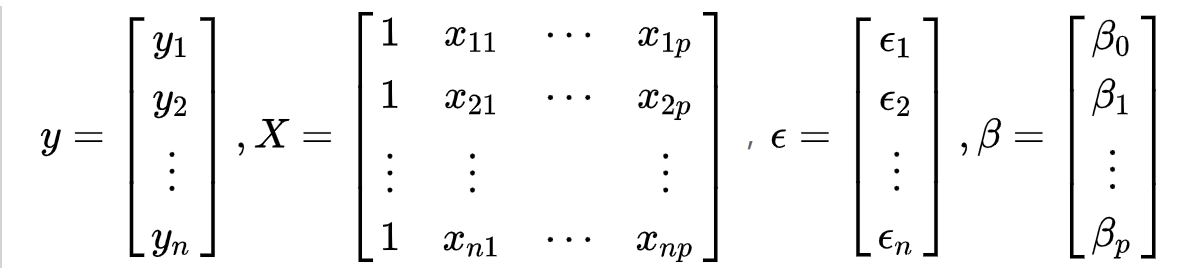

那么这个时候的多元线性回归的表示就变成了 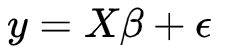，其中 我们一般称为设计矩阵。

1.数学原理

求解思路和一元线性回归法相同。
三维空间线性方程是
由此推到多维空间的形式

• 目标：使尽可能小。

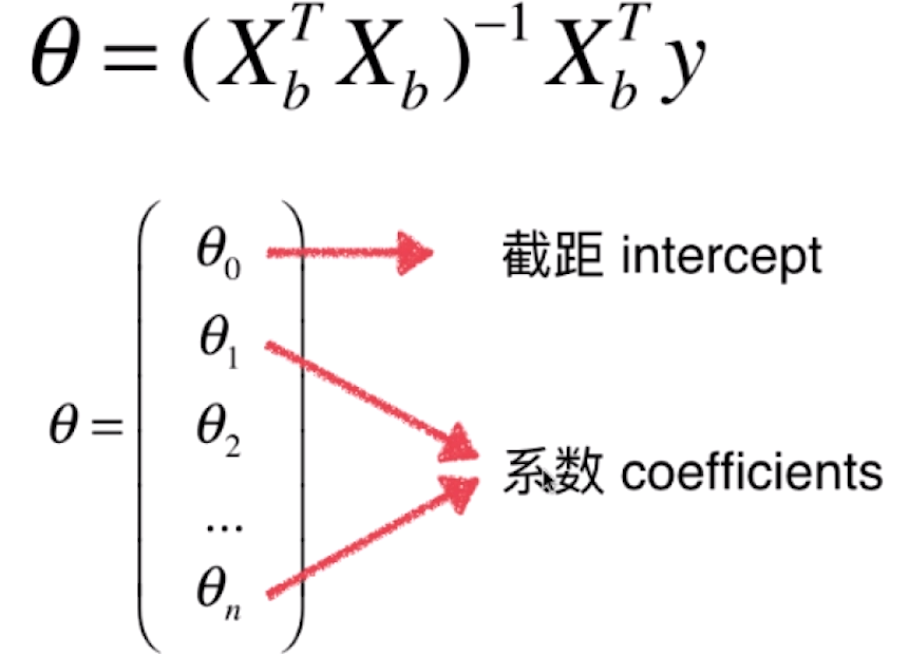
即找到，使得尽可能小。


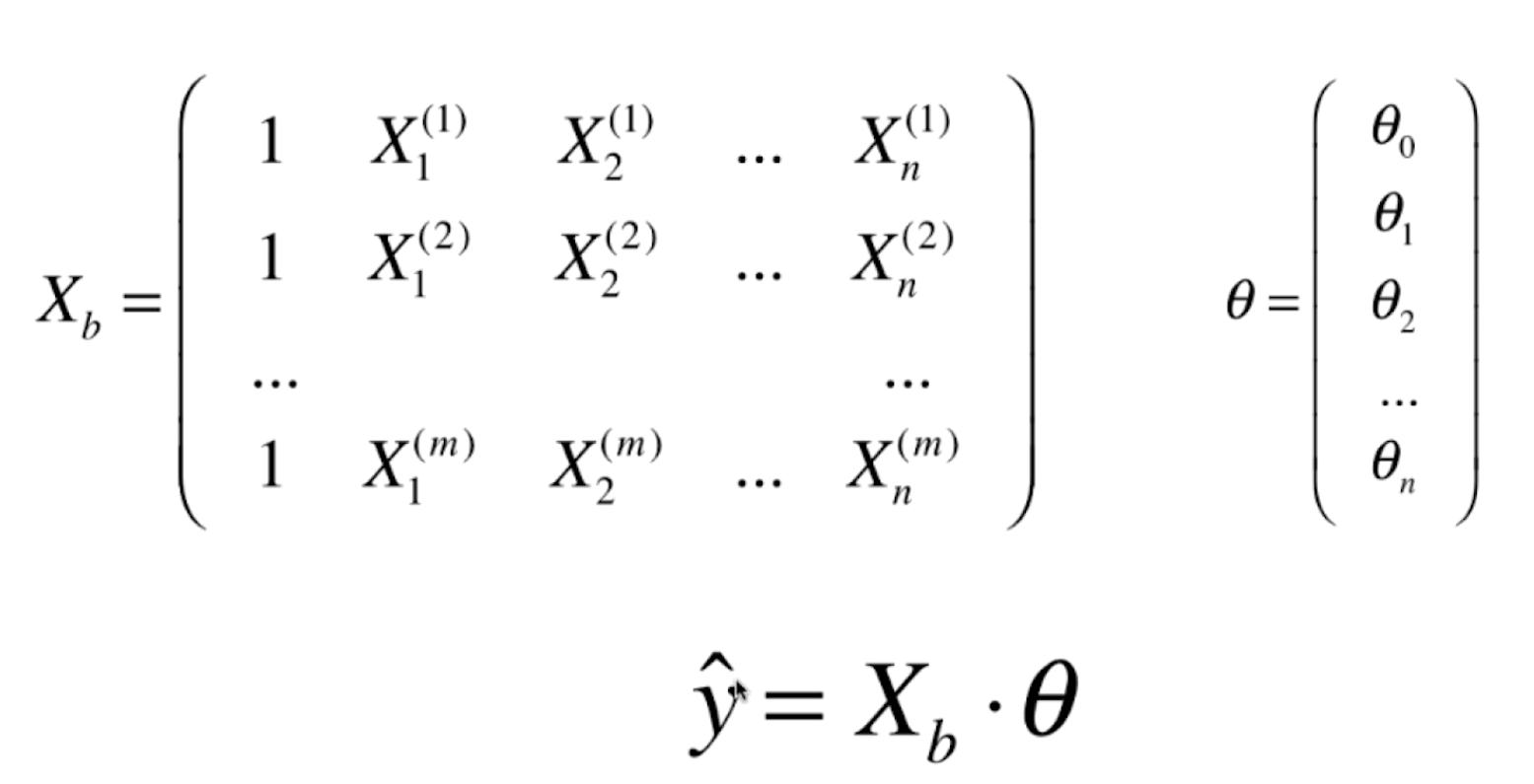
目标使 尽可能小，

• 问题：时间复杂度高： 优化 ，必要时需要使用 梯度下降法。
• 优点：不存在量纲问题，不需要对数据做归一化处理。( 由公式 可知，原来的数据进行矩阵运算，因此不存在量纲的问题 )
• 

2.封装模型

# LinearRegression.py
import numpy as np
from .metrics import r2_score
class LinearRegression:
    def __init__(self):
        """初始化Linear Regression模型"""
        self.coef_ = None
        self.intercept_ = None
        self._theta = None
    def fit_normal(self, X_train, y_train):
        """根据训练数据集X_train, y_train训练Linear Regression模型"""
        assert X_train.shape[0] == y_train.shape[0], \
            "the size of X_train must be equal to the size of y_train"
        X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
        self._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)
        self.intercept_ = self._theta[0]
        self.coef_ = self._theta[1:]
        return self
    def predict(self, X_predict):
        """给定待预测数据集X_predict，返回表示X_predict的结果向量"""
        assert self.intercept_ is not None and self.coef_ is not None, \
            "must fit before predict!"
        assert X_predict.shape[1] == len(self.coef_), \
            "the feature number of X_predict must be equal to X_train"
        X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])
        return X_b.dot(self._theta)
    def score(self, X_test, y_test):
        """根据测试数据集 X_test 和 y_test 确定当前模型的准确度"""
        y_predict = self.predict(X_test)
        return r2_score(y_test, y_predict)
    def __repr__(self):
        return "LinearRegression()"

3.编码实现

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
boston = datasets.load_boston()
X = boston.data
y = boston.target
X = X[y < 50.0]
y = y[y < 50.0]
X.shape  # (490, 13)
# 切分数据集
from playML.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, seed=666)
# 建模
from playML.LinearRegression import LinearRegression
reg = LinearRegression()
reg.fit_normal(X_train, y_train)
reg.coef_
# array([-1.18919477e-01,  3.63991462e-02, -3.56494193e-02,  5.66737830e-02,
#       -1.16195486e+01,  3.42022185e+00, -2.31470282e-02, -1.19509560e+00,
#        2.59339091e-01, -1.40112724e-02, -8.36521175e-01,  7.92283639e-03,
#       -3.81966137e-01])
reg.intercept_  # 34.16143549625432
reg.score(X_test, y_test)  # 模型打分： 0.812980260265854

4.scikit-learn实现

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
# 加载数据
boston = datasets.load_boston()
X = boston.data
y = boston.target
# 数据预处理
X = X[y < 50.0]
y = y[y < 50.0]
X.shape  # (490, 13)
from playML.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, seed=666)
# 建模
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X_train, y_train)
# LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
lin_reg.coef_
# array([-1.18919477e-01,  3.63991462e-02, -3.56494193e-02,  5.66737830e-02,
#       -1.16195486e+01,  3.42022185e+00, -2.31470282e-02, -1.19509560e+00,
#        2.59339091e-01, -1.40112724e-02, -8.36521175e-01,  7.92283639e-03,
#       -3.81966137e-01])
lin_reg.intercept_  # 34.16143549624639
lin_reg.score(X_test, y_test)  # 0.8129802602658499

5.KNN解决回归问题

from sklearn.preprocessing import StandardScaler
# 数据预处理
standardScaler = StandardScaler()
standardScaler.fit(X_train, y_train)
X_train_standard = standardScaler.transform(X_train)
X_test_standard = standardScaler.transform(X_test)
# 建模
from sklearn.neighbors import KNeighborsRegressor
knn_reg = KNeighborsRegressor()
knn_reg.fit(X_train_standard, y_train)
knn_reg.score(X_test_standard, y_test)
# 网格搜索
from sklearn.model_selection import GridSearchCV
param_grid = [
    {
        "weights": ["uniform"],
        "n_neighbors": [i for i in range(1, 11)]
    },
    {
        "weights": ["distance"],
        "n_neighbors": [i for i in range(1, 11)],
        "p": [i for i in range(1,6)]
    }
]
knn_reg = KNeighborsRegressor()
grid_search = GridSearchCV(knn_reg, param_grid, n_jobs=-1, verbose=1)  # n_jobs=-1 代码使用所有CPU核
grid_search.fit(X_train_standard, y_train)
# Fitting 3 folds for each of 60 candidates, totalling 180 fits
# GridSearchCV(cv=None, error_score='raise',
#        estimator=KNeighborsRegressor(algorithm='auto', leaf_size=30, metric='minkowski',
#           metric_params=None, n_jobs=1, n_neighbors=5, p=2,
#           weights='uniform'),
#        fit_params=None, iid=True, n_jobs=-1,
#         param_grid=[{'weights': ['uniform'], 'n_neighbors': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]}, {'weights': ['distance'], 
# 'n_neighbors': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10], 'p': [1, 2, 3, 4, 5]}],
#        pre_dispatch='2*n_jobs', refit=True, return_train_score='warn',
#        scoring=None, verbose=1)
grid_search.best_params_  # 最好结果 {'n_neighbors': 5, 'p': 1, 'weights': 'distance'}
grid_search.best_score_  # 评分： 0.799179998909969
grid_search.best_estimator_.score(X_test_standard, y_test)  # 0.880996650994177