• 一种基于搜索的最优化方法
• 不是一个机器学习算法
• 作用：优化/最小化目标函数
• 梯度上升法：最大化一个效用函数

原理：

• 导数代表J增大的方向。（为正）
• 这里涉及到数学基础是方向导数；(方向导数 可由全微分证出，可由偏导数表示)

方向导数可以用偏导数表示，偏导数可以抽象出 梯度的概念，梯度其实就是一个向量，方向导数和偏导数是一个数。

1. 偏导数表示 方向导数： （1式）
2. 数量积表示上式： （2式）
3. 从上式抽象出梯度概念： （3式）

从公式的 1式 到 3式 的演变可知，梯度其实是个为了在多维空间方便表示和函数方向的一种概念而已。

一元函数的梯度解析图

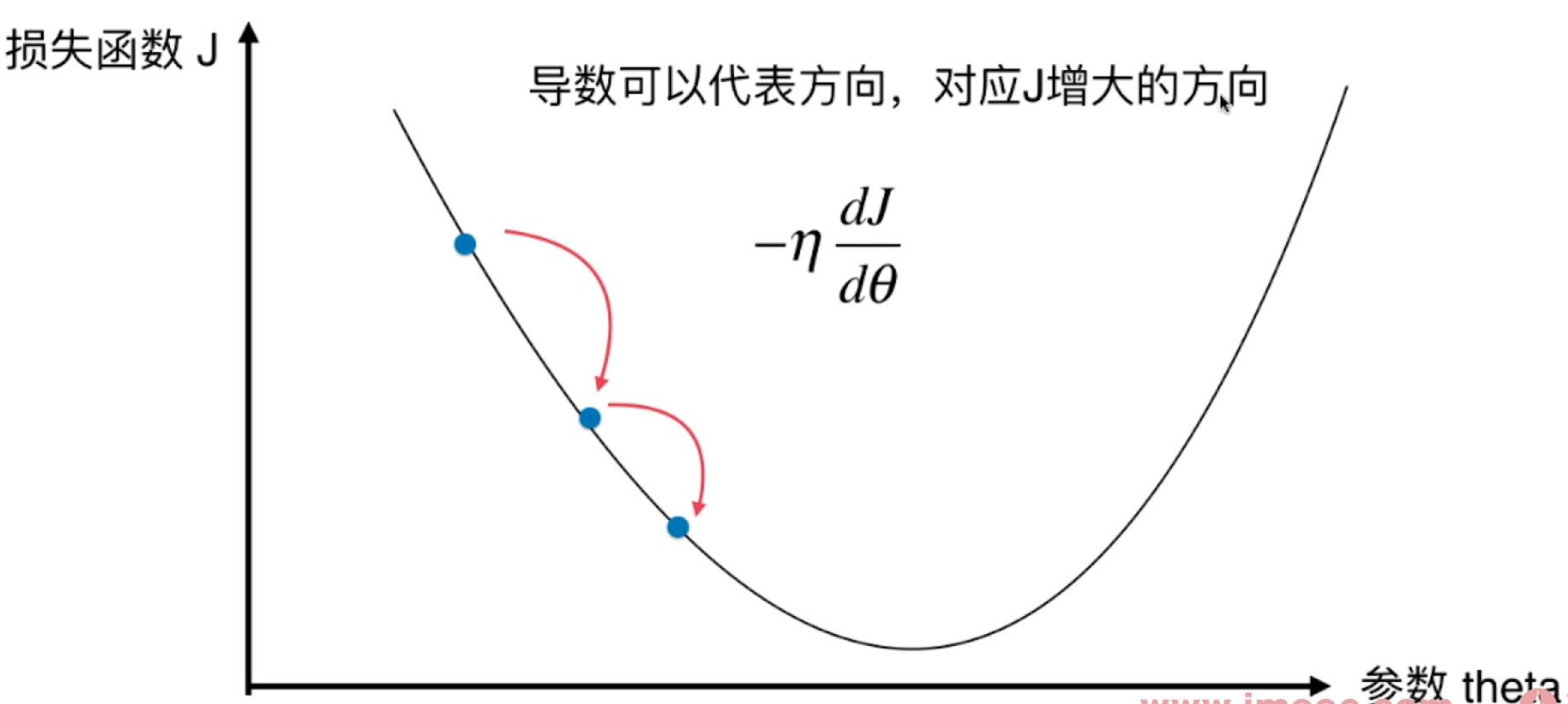
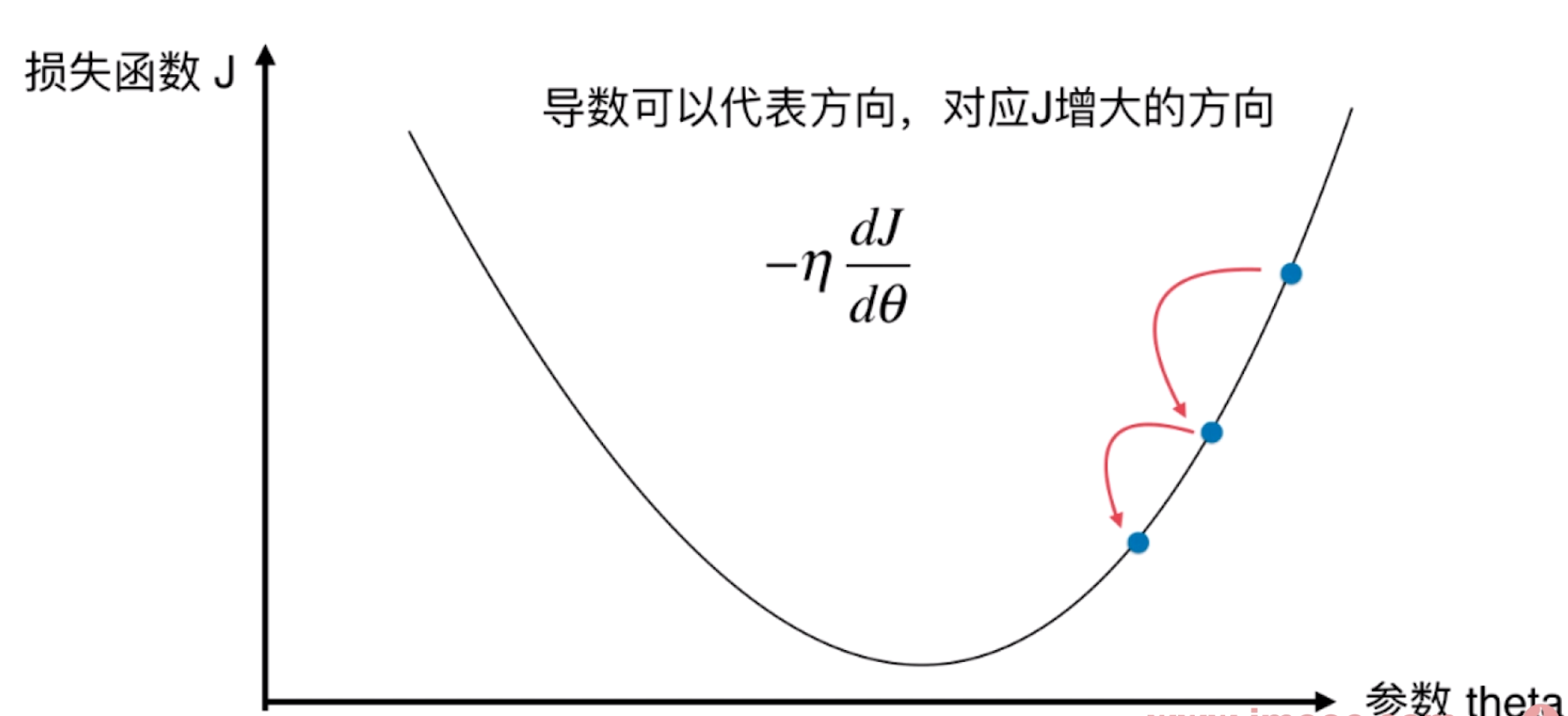
• 称为学习率
• 是梯度下降的一个超参数
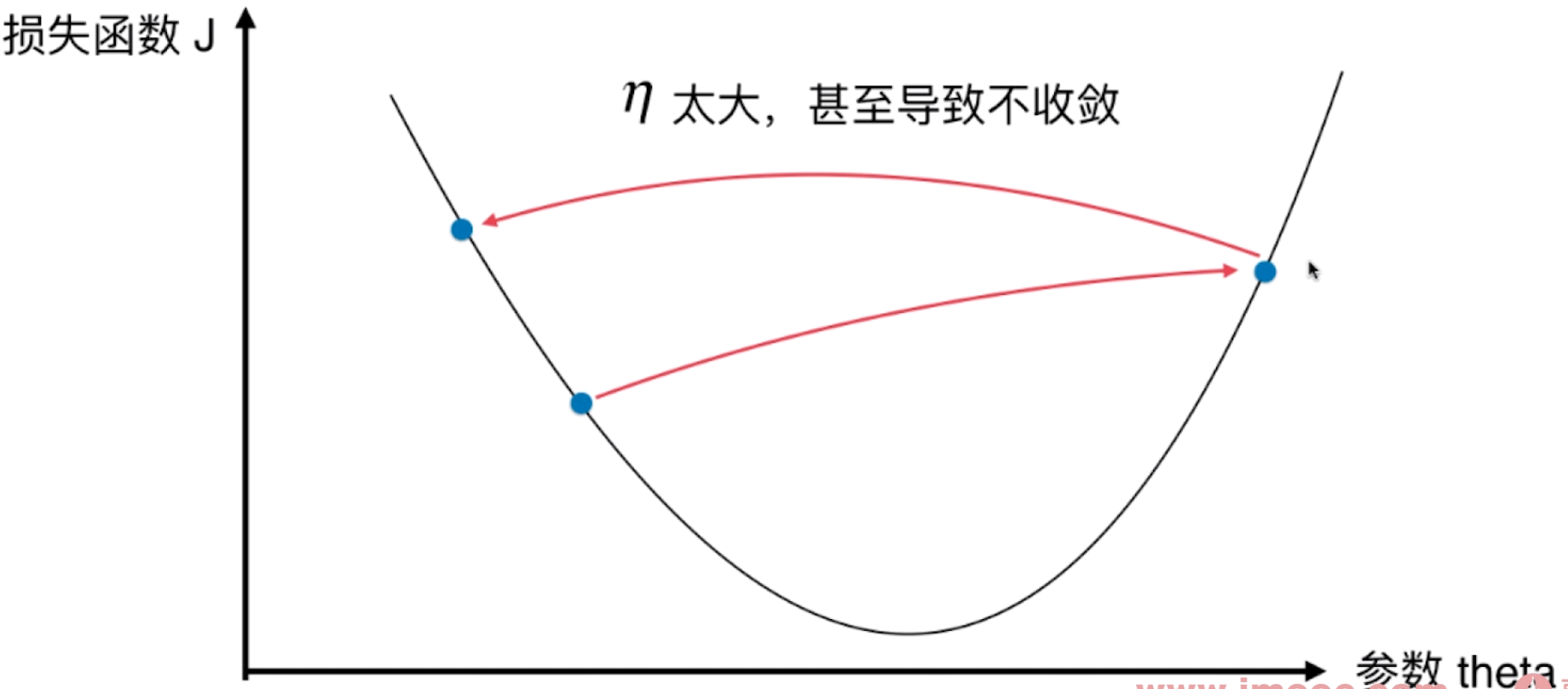
• 的取值影响获得最优解的速度

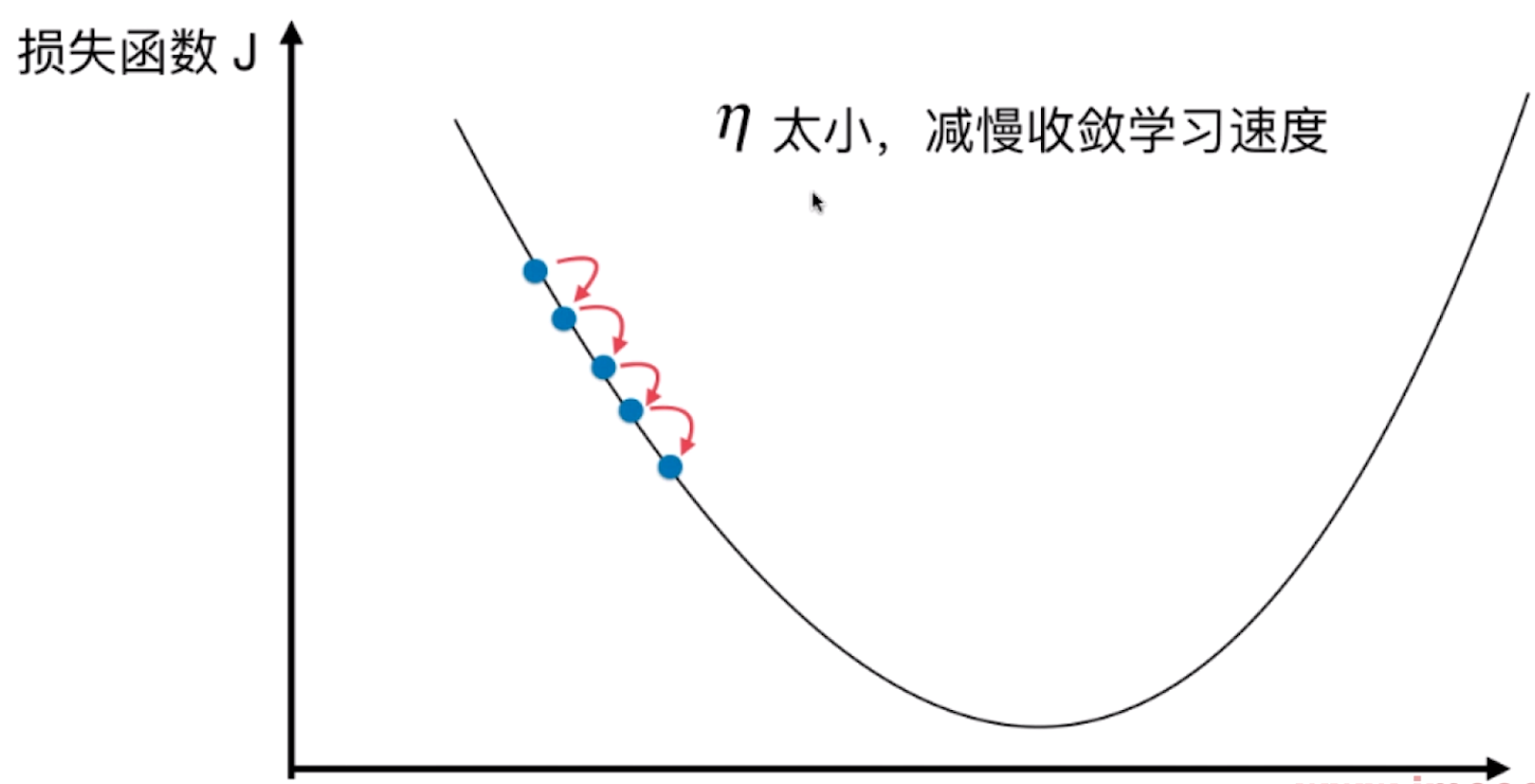
• 取值不合适，甚至得不到最优解

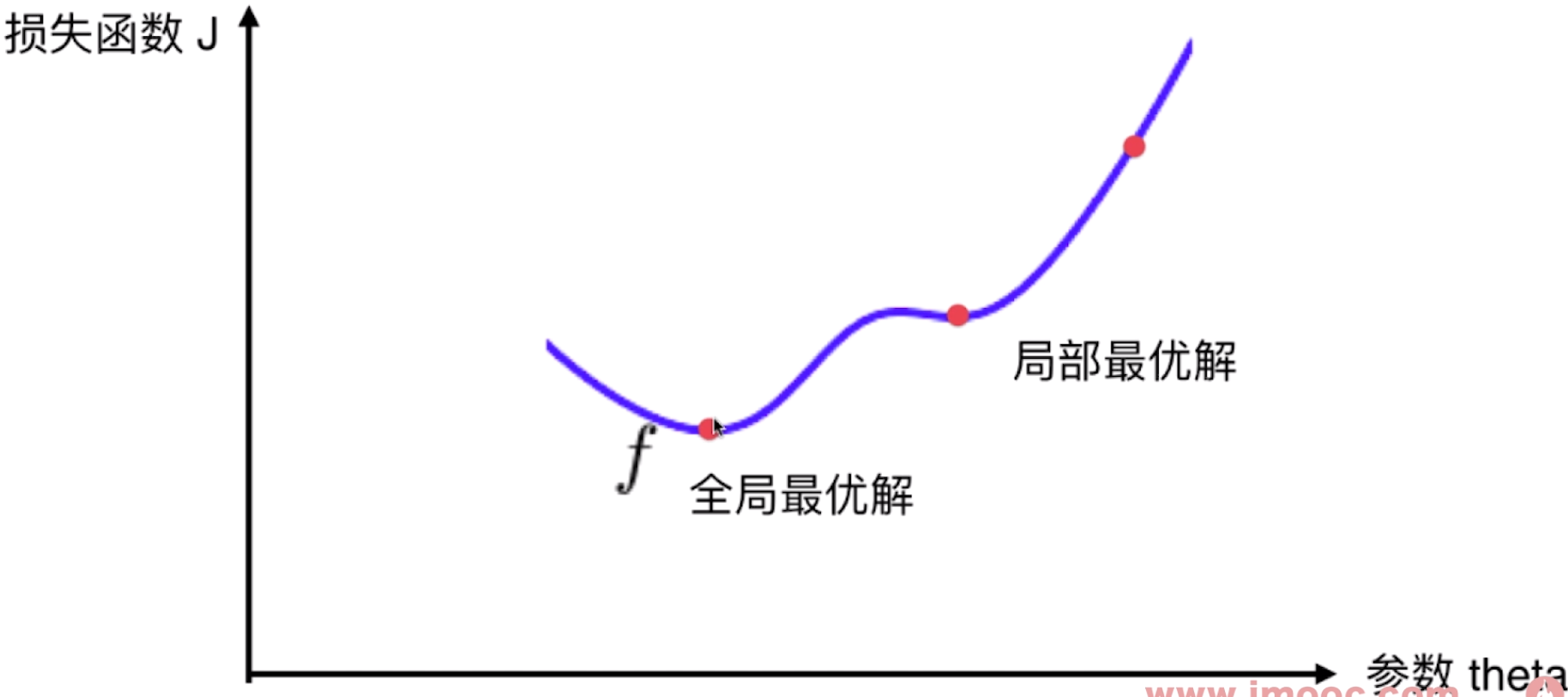
• 极值点可能不唯一

上面举的例子是只有一个最优解，但实际情况可能有多个驻点(极值点)。
解决方案：多次运行，随机化初始点（梯度下降的初始点也是一个超参数）