描述

路径 被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例

示例1：

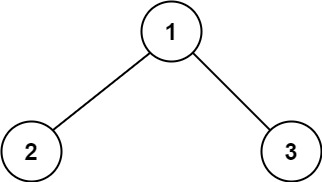
exx1.jpg

  1. 输入：root = [1,2,3]
  2. 输出：6
  3. 解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例2：

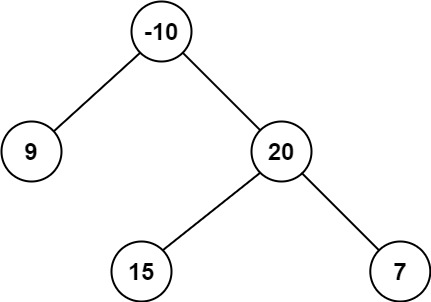
exx2.jpg

输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

提示

  • 树中节点数目范围是 [1, 3 * 104]
  • -1000 <= Node.val <= 1000

解题思路

二叉树 abc，a 是根结点（递归中的 root），bc 是左右子结点（代表其递归后的最优解）。
最大的路径，可能的路径情况：

    a
   / \
  b   c
  1. b + a + c。
  2. b + a + a 的父结点。
  3. a + c + a 的父结点。

其中情况 1，表示如果不联络父结点的情况，或本身是根结点的情况。
这种情况是没法递归的，但是结果有可能是全局最大路径和。
情况 2 和 3，递归时计算 a+b 和 a+c，选择一个更优的方案返回，也就是上面说的递归后的最优解啦。

另外结点有可能是负值，最大和肯定就要想办法舍弃负值（max(0, x))。
但是上面 3 种情况，无论哪种，a 作为联络点，都不能够舍弃。

代码

class Solution {
    int maxSum = Integer.MIN_VALUE;

    public int maxPathSum(TreeNode root) {
        maxGain(root);
        return maxSum;
    }

    public int maxGain(TreeNode node) {
        if (node == null) {
            return 0;
        }

        // 递归计算左右子节点的最大贡献值
        // 只有在最大贡献值大于 0 时，才会选取对应子节点
        int leftGain = Math.max(maxGain(node.left), 0);
        int rightGain = Math.max(maxGain(node.right), 0);

        // 节点的最大路径和取决于该节点的值与该节点的左右子节点的最大贡献值
        int priceNewpath = node.val + leftGain + rightGain;

        // 更新答案
        maxSum = Math.max(maxSum, priceNewpath);

        // 返回节点的最大贡献值
        return node.val + Math.max(leftGain, rightGain);
    }
}

复杂度分析

时间复杂度：O(N)，其中 N 是二叉树中的节点个数。对每个节点访问不超过 2 次。
空间复杂度：O(N)，其中 N 是二叉树中的节点个数。空间复杂度主要取决于递归调用层数，最大层数等于二叉树的高度，最坏情况下，二叉树的高度等于二叉树中的节点个数。