- 剑指 Offer 07. 重建二叉树">剑指 Offer 07. 重建二叉树
- 剑指 Offer 26. 树的子结构">剑指 Offer 26. 树的子结构
- 剑指 Offer 27. 二叉树的镜像">剑指 Offer 27. 二叉树的镜像
- 剑指 Offer 28. 对称的二叉树">剑指 Offer 28. 对称的二叉树
- 剑指 Offer 32 - I. 从上到下打印二叉树">剑指 Offer 32 - I. 从上到下打印二叉树
- 剑指 Offer 32 - II. 从上到下打印二叉树 II">剑指 Offer 32 - II. 从上到下打印二叉树 II
- 剑指 Offer 32 - III. 从上到下打印二叉树 III">剑指 Offer 32 - III. 从上到下打印二叉树 III
- 剑指 Offer 33. 二叉搜索树的后序遍历序列">剑指 Offer 33. 二叉搜索树的后序遍历序列
- 剑指 Offer 36. 二叉搜索树与双向链表">剑指 Offer 36. 二叉搜索树与双向链表
- 剑指 Offer 37. 序列化二叉树">剑指 Offer 37. 序列化二叉树
- 剑指 Offer 54. 二叉搜索树的第k大节点">剑指 Offer 54. 二叉搜索树的第k大节点
- 剑指 Offer 55 - I. 二叉树的深度">剑指 Offer 55 - I. 二叉树的深度
- 剑指 Offer 55 - II. 平衡二叉树">剑指 Offer 55 - II. 平衡二叉树
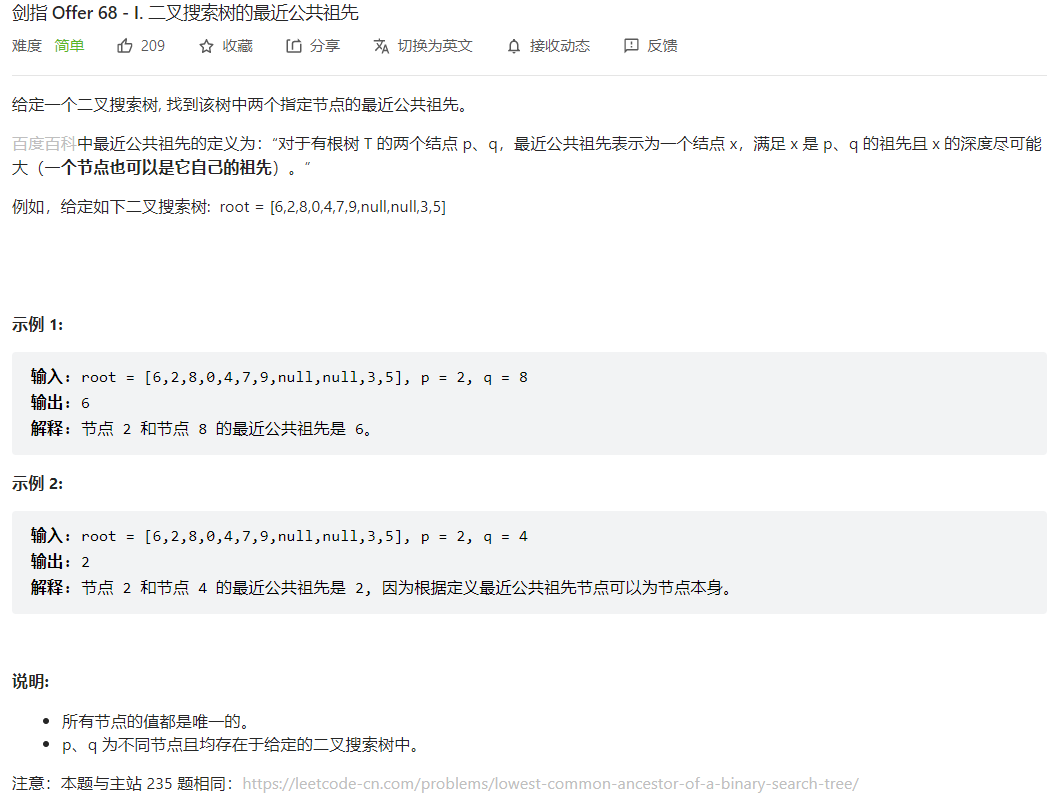
- 剑指 Offer 68 - I. 二叉搜索树的最近公共祖先">剑指 Offer 68 - I. 二叉搜索树的最近公共祖先
- 剑指 Offer 68 - II. 二叉树的最近公共祖先">剑指 Offer 68 - II. 二叉树的最近公共祖先
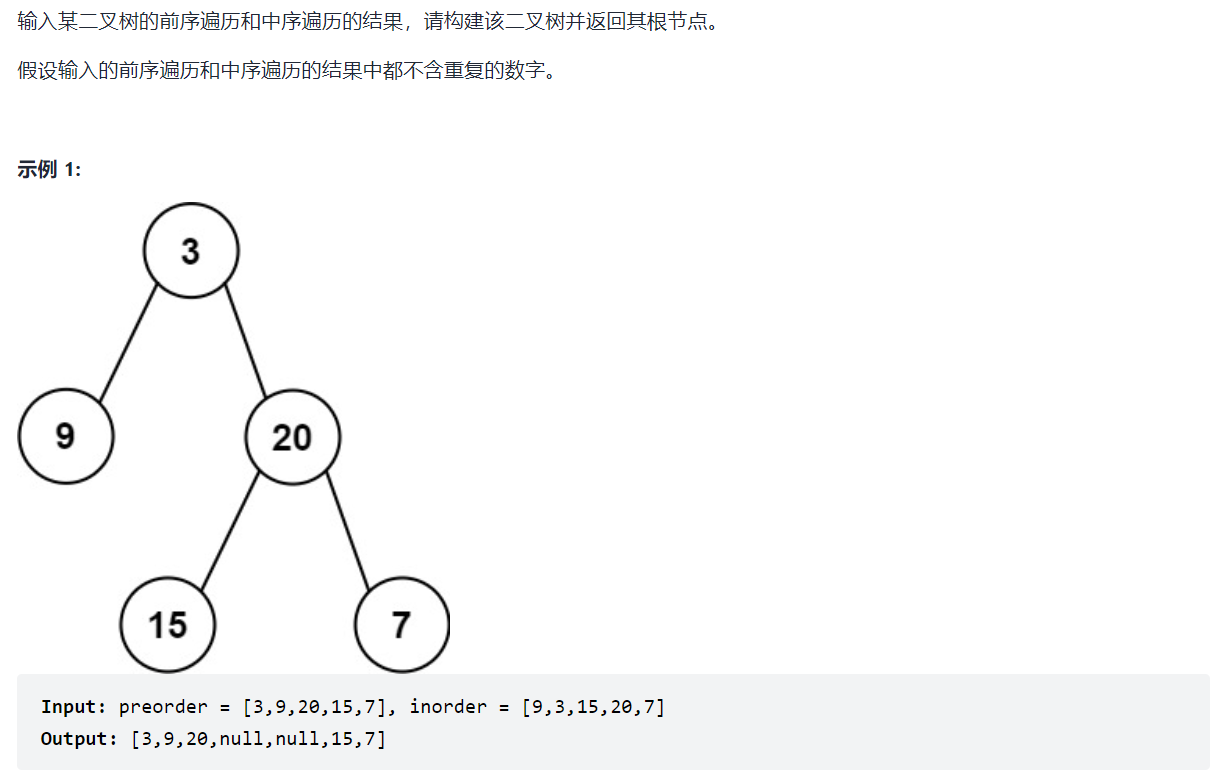
剑指 Offer 07. 重建二叉树

/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/class Solution {public:TreeNode* build(vector<int>& preorder, int pbeg, int pend, vector<int>& inorder, int ibeg, int iend) {if (pbeg >= pend) return NULL;// construt rootTreeNode* root = new TreeNode(preorder[pbeg]);if (pend - pbeg == 1) return root;// find the element index in inorderint index = ibeg;while (index < iend) {if (inorder[index] == preorder[pbeg]) {break;}index++;}// recursion construct left and right childroot->left = build(preorder, pbeg + 1, pbeg + index - ibeg + 1, inorder, ibeg, index);root->right = build(preorder, pbeg + index - ibeg + 1, pend, inorder, index + 1, iend);return root;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {return build(preorder, 0, preorder.size(), inorder, 0, inorder.size());}};
剑指 Offer 26. 树的子结构
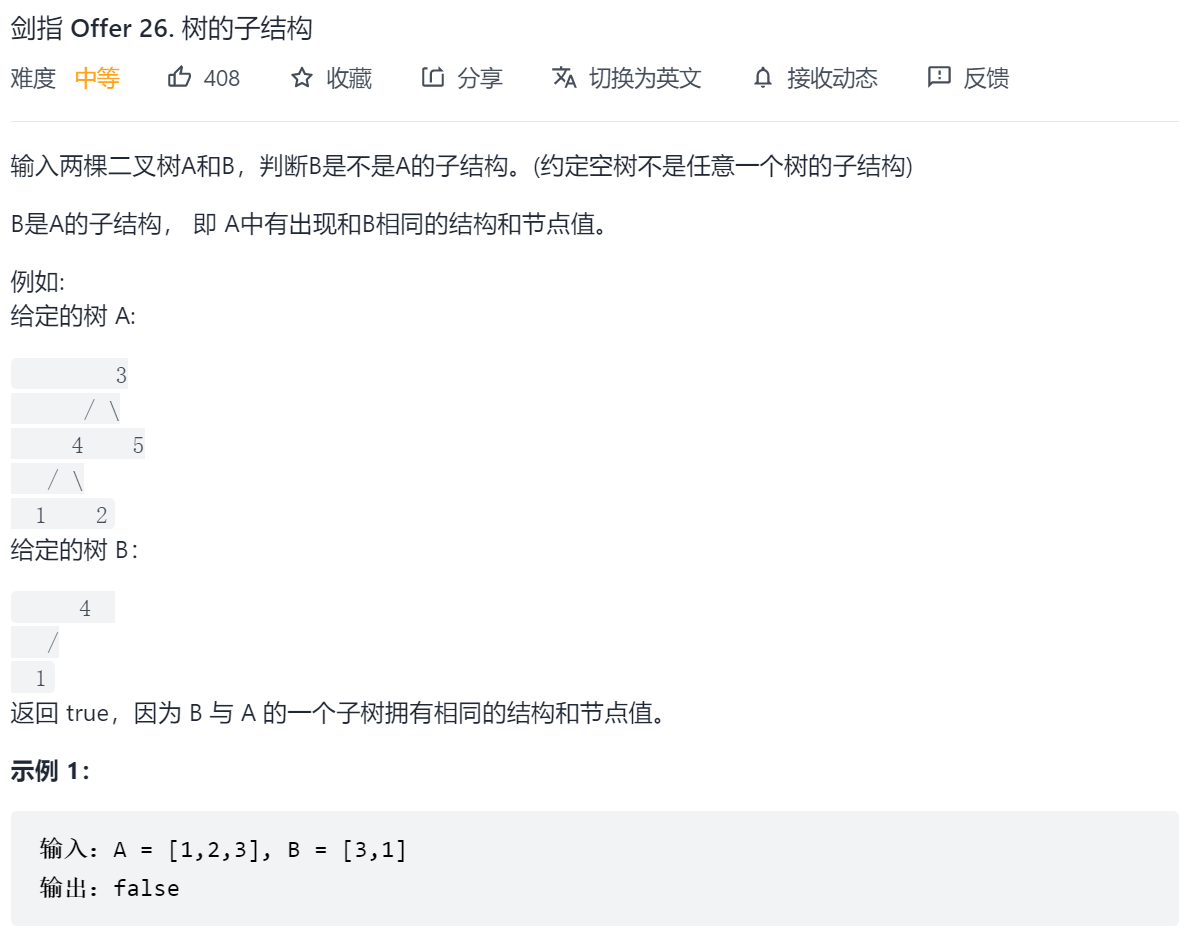
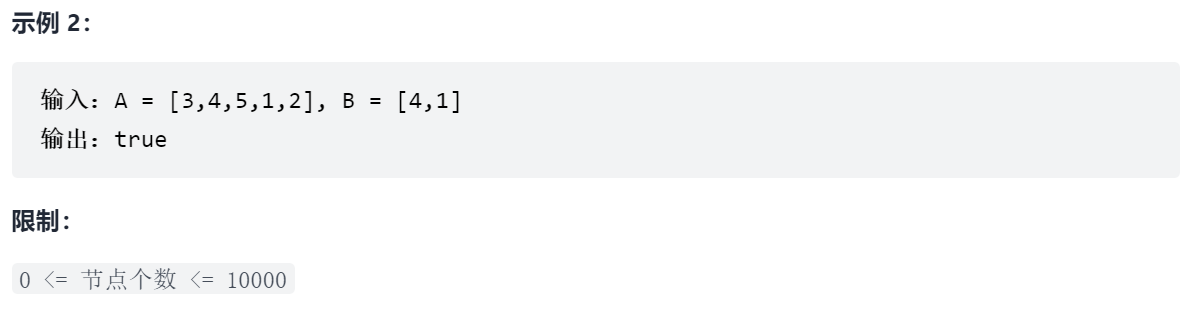
这一题采用先序遍历,要判断B是否为A的子树,需要两个步骤:
- 先序遍历A,依次处理某节点
- 从树的某一个节点出发,判断能否找到一个与B一致的结构
所以需要一个辅助函数,来比较以一个节点为根的子树是否能够找到B
bool isContain(TreeNode* A, TreeNode* B) {
if (!B) return true; // 如果B是空的,那么包含
if (!A || A->val != B->val) // 当前节点为空或者值与B中对应节点的值不相等,返回false
return false;
return isContain(A->left, B->left) && isContain(A->right, B->right); 左右子孩子必须都匹配上,才返回true
}
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
bool isSubStructure(TreeNode* A, TreeNode* B) {
if (!A || !B) return false; // 空节点不是任何树的子结构
return isContain(A, B) || isSubStructure(A->left, B) || isSubStructure(A->right, B); //先序遍历
}
bool isContain(TreeNode* A, TreeNode* B) {
if (!B) return true;
if (!A || A->val != B->val)
return false;
return isContain(A->left, B->left) && isContain(A->right, B->right);
}
};
剑指 Offer 27. 二叉树的镜像
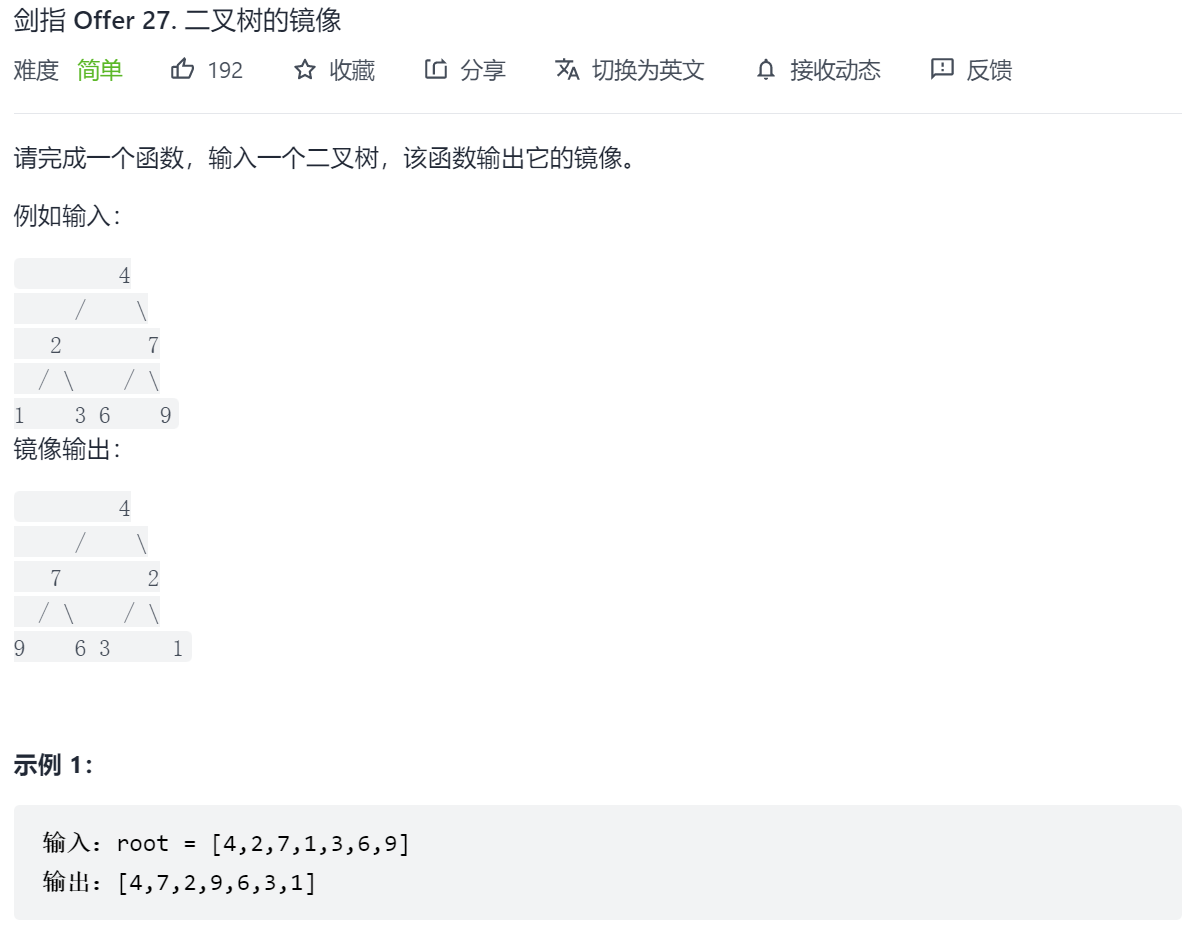
后序遍历即可。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* mirrorTree(TreeNode* root) {
// 后序遍历
if (!root) return root;
TreeNode* left = mirrorTree(root->left);
TreeNode* right = mirrorTree(root->right);
root->left = right;
root->right = left;
return root;
}
};
剑指 Offer 28. 对称的二叉树


因为是比较镜像位置的节点是否相同,所以递归比较左子树的左孩子和右子树的有孩子、左子树的右孩子和右子树的左孩子是否相同
因此要定义一个函数,用来判断两个节点是否相同,不同的情况:
- 一个为空
- 数值不同
两个节点都空,或者数值相同,那么两个节点相同
接下来按照对称的顺序比较节点即可
class Solution {
public:
bool compare(TreeNode* left, TreeNode* right) {
// 两个都是空节点那么返回true
if (left == NULL && right == NULL)
return true;
if (left == NULL || right == NULL || left->val != right->val)
return false;
return compare(left->left, right->right) && compare(left->right, right->left);
}
bool isSymmetric(TreeNode* root) {
if (root == NULL)
return true;
return compare(root->left, root->right);
}
};
简略版本
class Solution {
public:
bool compare(TreeNode* left, TreeNode* right) {
if (!left && !right) return true;
if (!left || !right || left->val != right->val)
return false;
return compare(left->left, right->right) && compare(left->right, right->left);
}
bool isSymmetric(TreeNode* root) {
if (root == NULL) return true;
return compare(root->left, root->right);
}
};
剑指 Offer 32 - I. 从上到下打印二叉树
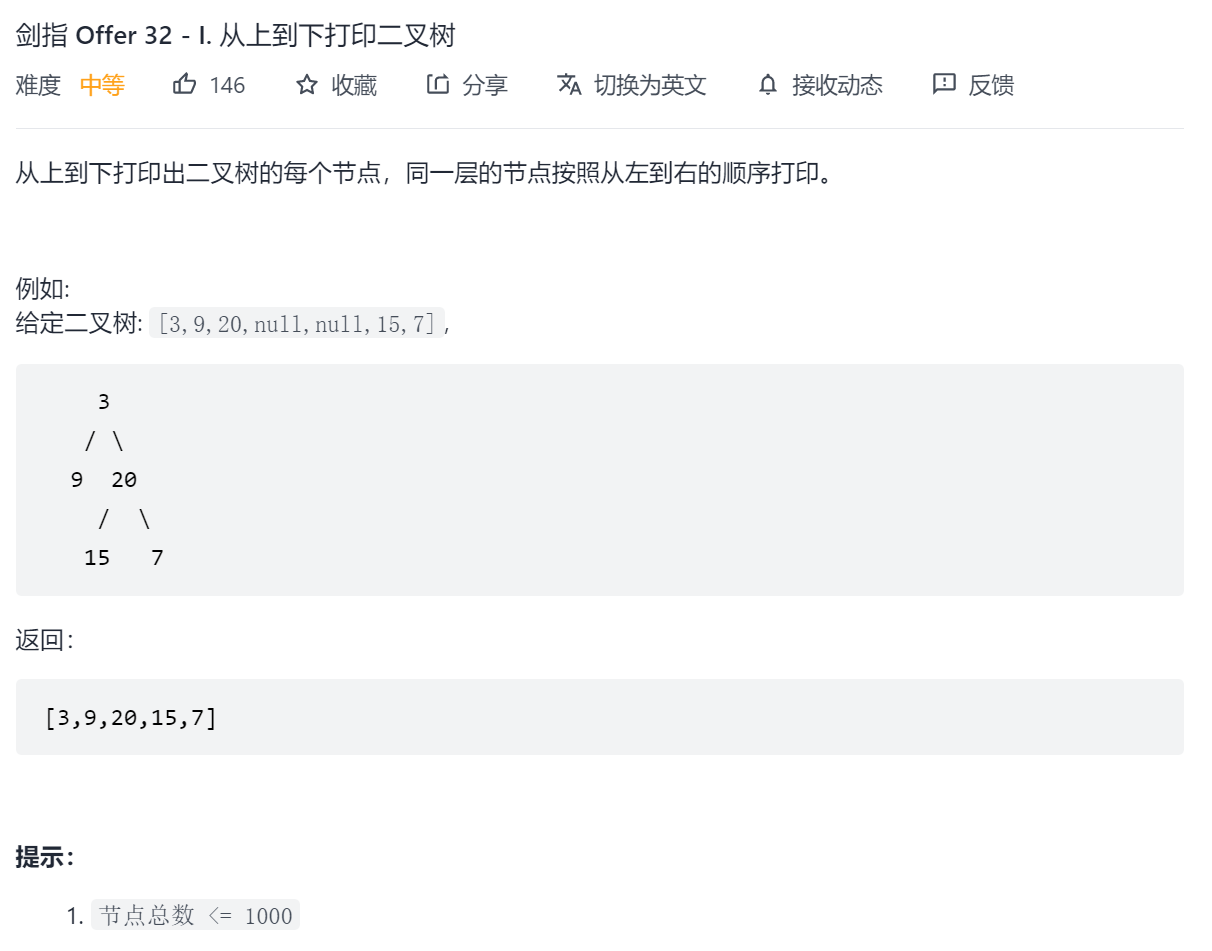
此题考察二叉树的层序遍历,比较简单
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<int> levelOrder(TreeNode* root) {
if (!root) return {};
queue<TreeNode*> que;
TreeNode* cur = root;
vector<int> res;
que.push(cur);
while (!que.empty()) {
int size = que.size();
for (int i = 0; i < size; i++) {
cur = que.front();
res.push_back(cur->val);
if (cur->left) que.push(cur->left);
if (cur->right) que.push(cur->right);
que.pop();
}
}
return res;
}
};
剑指 Offer 32 - II. 从上到下打印二叉树 II
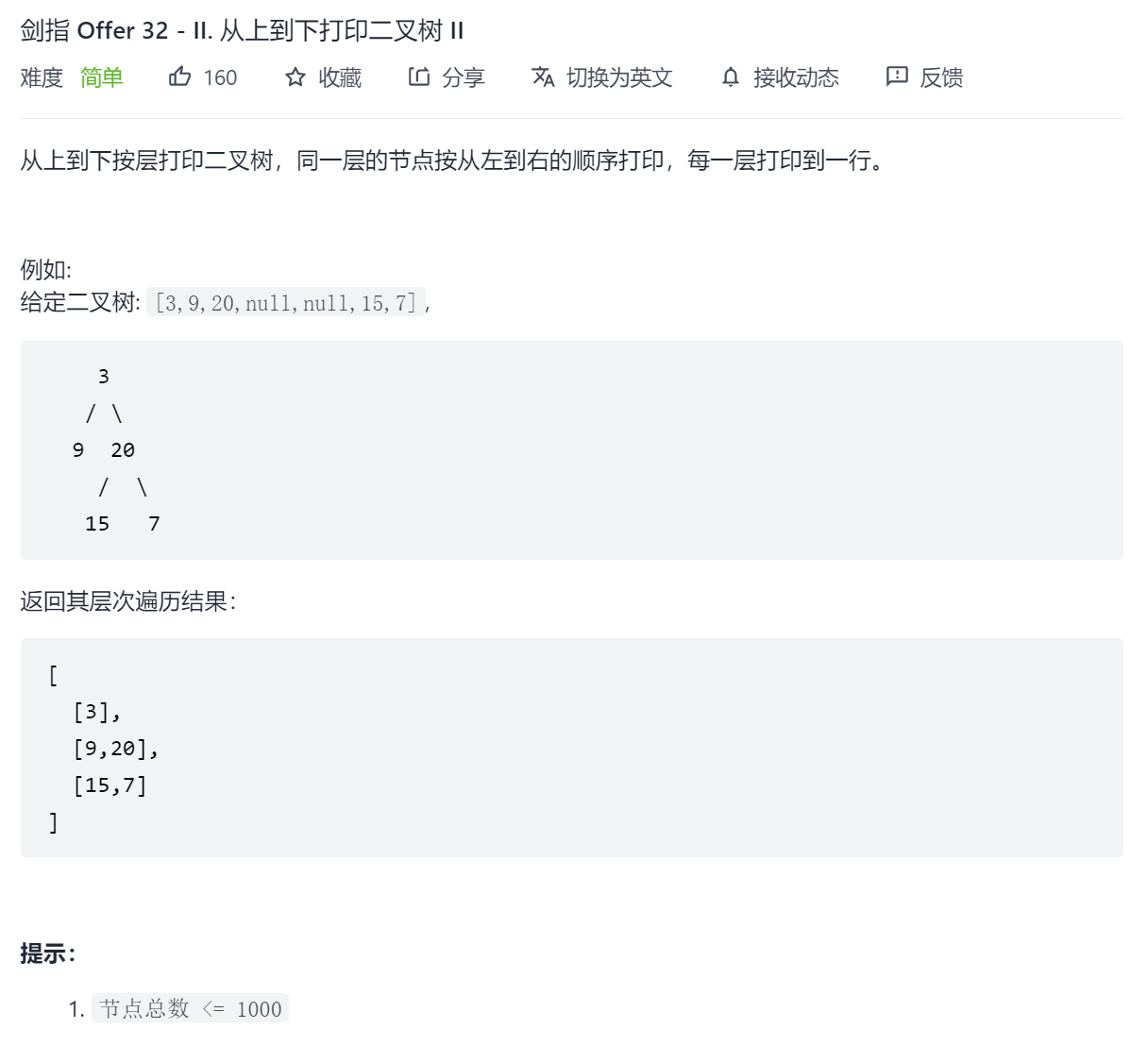
同样比较简单,只是输出形式稍作改变,套用层序遍历模板即可
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
if (root == NULL) return {};
queue<TreeNode*> que;
que.push(root);
vector<vector<int>> res;
while (!que.empty()) {
int size = que.size();
vector<int> layer;
for (int i = 0; i < size; i++) {
TreeNode* cur = que.front(); que.pop();
layer.push_back(cur->val);
if (cur->left != NULL) que.push(cur->left);
if (cur->right != NULL) que.push(cur->right);
}
res.push_back(layer);
}
return res;
}
};
剑指 Offer 32 - III. 从上到下打印二叉树 III
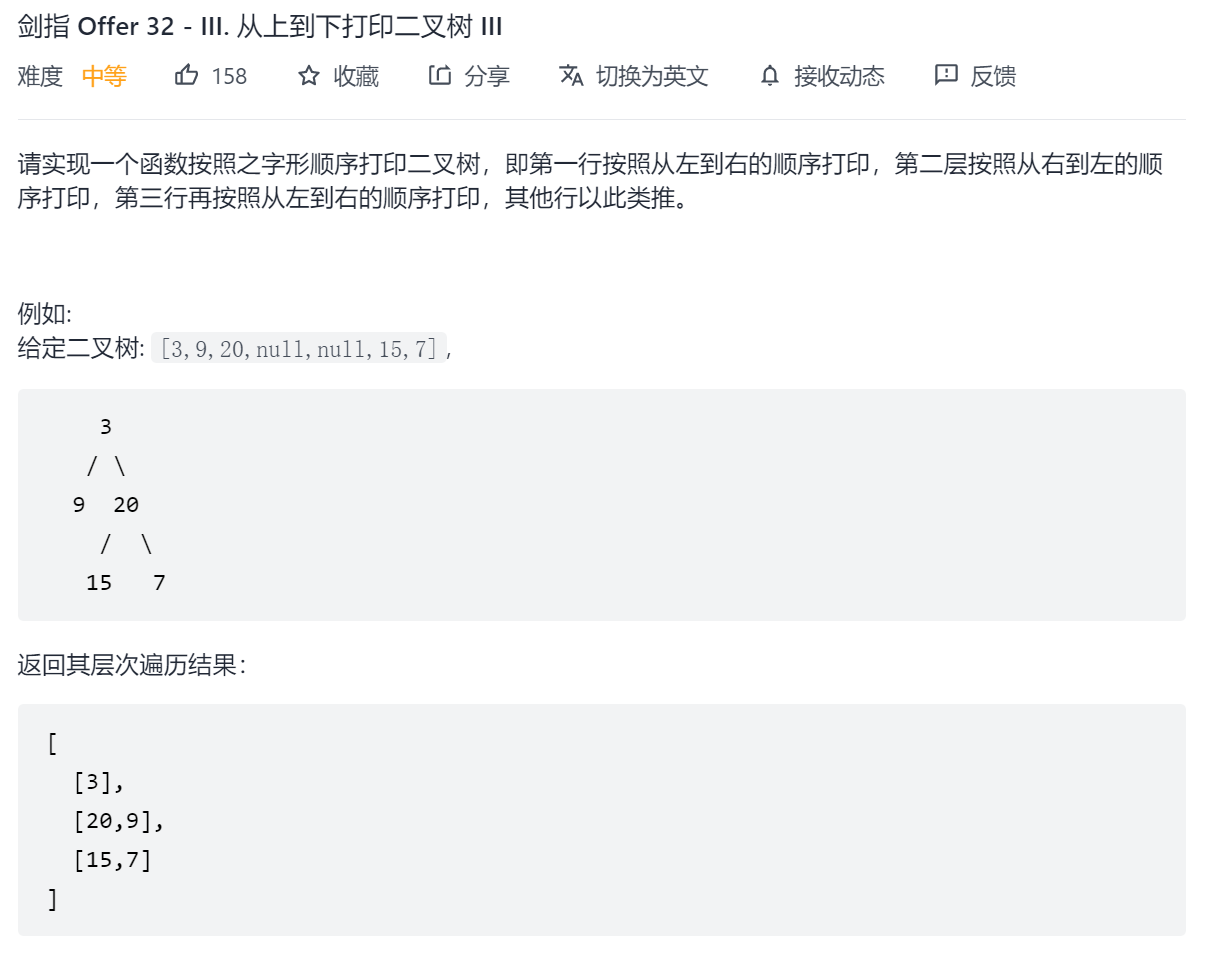
根据题意,套用模板,设置一个标志位,用来判断当前层的输出方向
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
if (!root) return {};
queue<TreeNode*> que;
TreeNode* cur = root;
vector<vector<int>> res;
que.push(cur);
bool flag = false; // true表示从左向右
while (!que.empty()) {
int size = que.size();
vector<int> level;
for (int i = 0; i < size; i++) {
cur = que.front();
level.push_back(cur->val);
if (cur->left) que.push(cur->left);
if (cur->right) que.push(cur->right);
que.pop();
}
if (flag) {
reverse(level.begin(), level.end());
}
flag = !flag;
res.push_back(level);
}
return res;
}
};
或者
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
if (root == NULL) return {};
queue<TreeNode*> que;
que.push(root);
vector<vector<int>> res;
while (!que.empty()) {
int size = que.size();
vector<int> layer;
for (int i = 0; i < size; i++) {
TreeNode* cur = que.front(); que.pop();
layer.push_back(cur->val);
if (cur->left != NULL) que.push(cur->left);
if (cur->right != NULL) que.push(cur->right);
}
res.push_back(layer);
}
for (int i = 1; i < res.size(); i += 2) {
reverse(res[i].begin(), res[i].end());
}
return res;
}
};
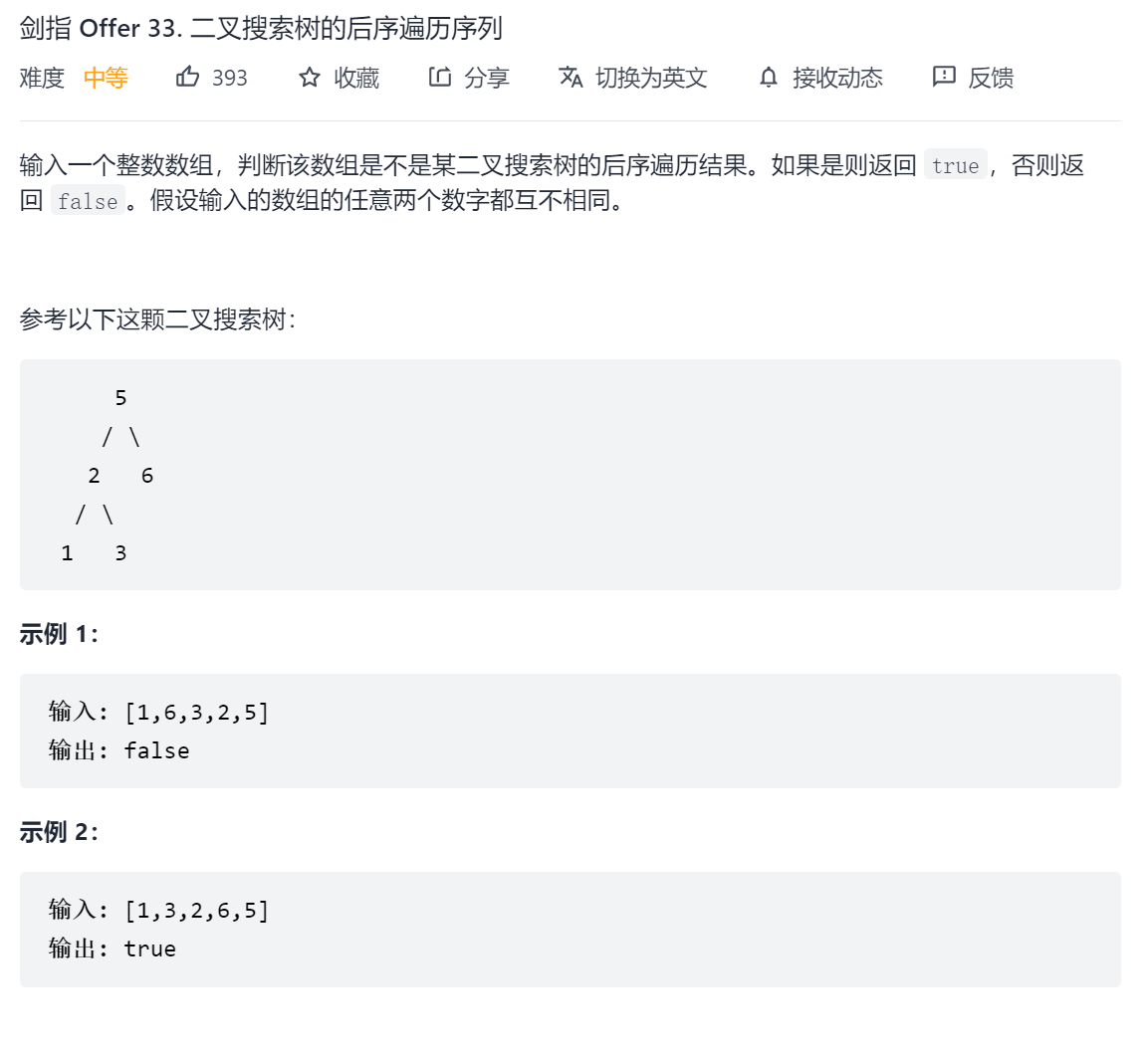
剑指 Offer 33. 二叉搜索树的后序遍历序列
分治+递归
二叉搜索树满足每个节点的左子树上的所有节点小于该节点,右子树上所有节点大于该节点
二叉搜索树的后序遍历,一定有最后一个节点的值是该树的“中间值”,可以根据这个特点,可以将数组不断划分为根 + 左子树 + 右子树,只有每个子树都是搜索树,整根树才是二叉搜索树
class Solution {
public:
bool divide(vector<int>& postorder, int begin, int end) {
if (begin >= end) { // 无节点可划分
return true;
}
int cur = begin;
// 找出以postorder[end]为根的左子树中的所有节点
while (postorder[cur] < postorder[end]) cur++;
// 找出以postorder[end]为根的右子树中的所有节点
int bound = cur;
while (postorder[cur] > postorder[end]) cur++;
// 递归处理左右子树
return cur == end && divide(postorder, begin, bound - 1) && divide(postorder, bound, cur - 1);
}
bool verifyPostorder(vector<int>& postorder) {
return divide(postorder, 0, postorder.size() - 1);
}
};
时间复杂度O(N)
单调栈(暂时跳过)
[
](https://leetcode-cn.com/problems/er-cha-sou-suo-shu-de-hou-xu-bian-li-xu-lie-lcof/solution/mian-shi-ti-33-er-cha-sou-suo-shu-de-hou-xu-bian-6/#:~:text=len(postorder)%20%2D%201)-,%E6%96%B9%E6%B3%95%E4%BA%8C%EF%BC%9A%E8%BE%85%E5%8A%A9%E5%8D%95%E8%B0%83,-%E6%A0%88)
剑指 Offer 36. 二叉搜索树与双向链表
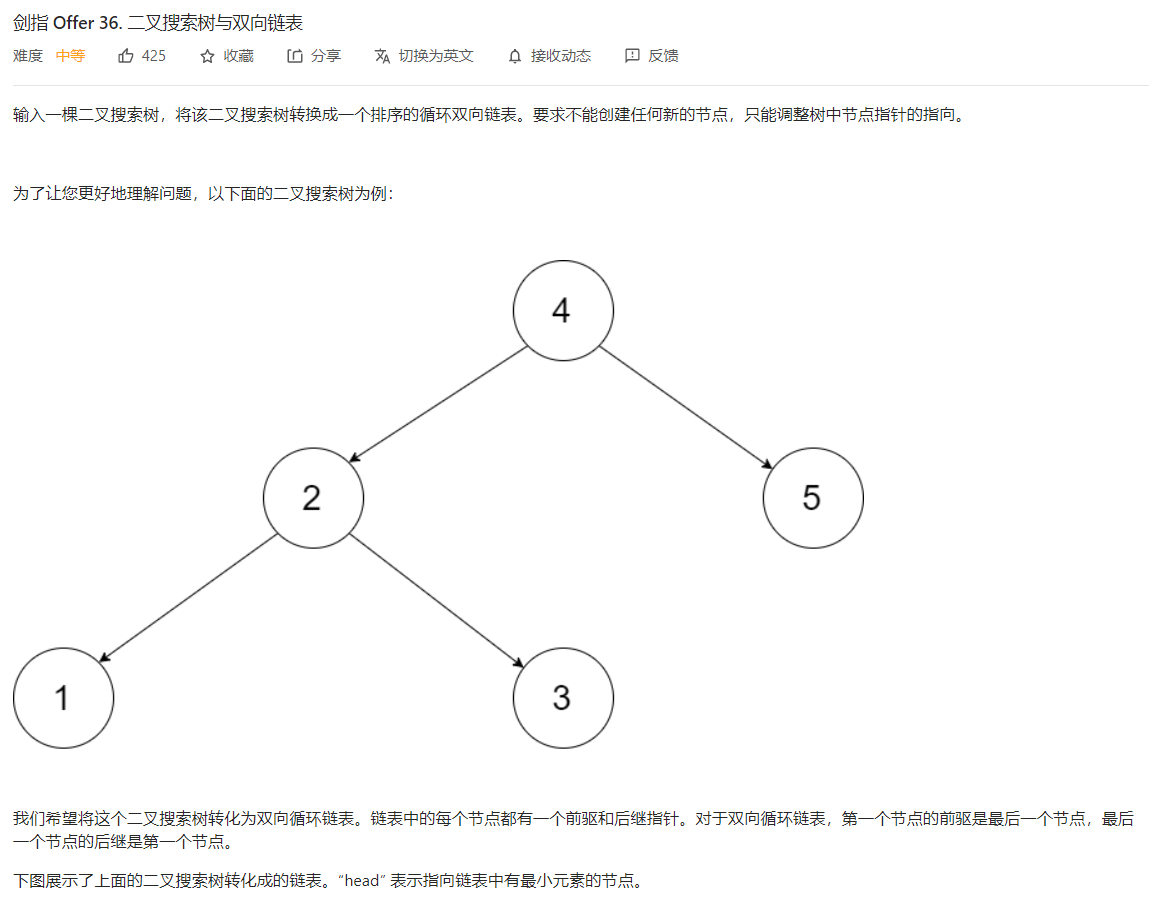
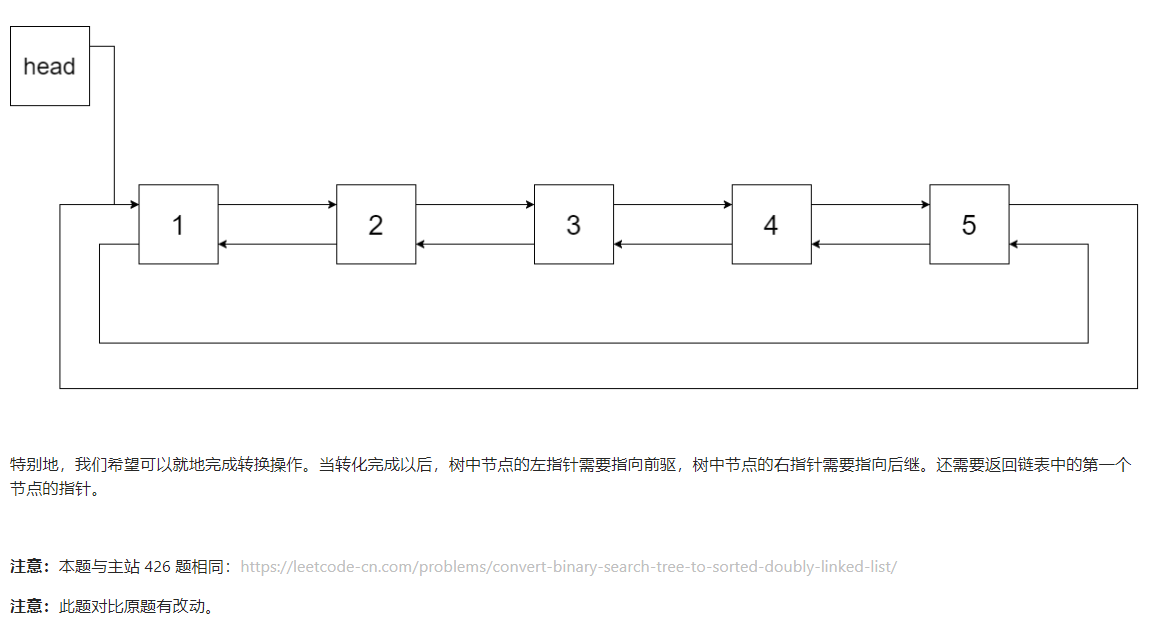
生成有序双链表,因为二叉搜索树中序遍历的结果为有序序列,因此本题采用中序遍历
中序遍历模板:
void inorder(Node* cur) {
if (!cur) return;
inorder(cur->left);
// 处理当前节点
// code
inorder(cur->right);
}
接下来修改中序遍历处理当前节点的部分
因为最后输出的链表为循环双链表,需要用一个节点pre记录上一个访问的节点,以便连接节点指向前驱节点的指针,节点的左孩子指针用来指向前驱节点,右孩子指针指向后继节点,双链表连接完成后,将头节点与尾节点连接,形成循环双链表
class Solution {
public:
Node* pre;
Node* head;
void inorder(Node* cur) {
if (!cur) return;
inorder(cur->left);
// 处理当前节点
if (pre != NULL) pre->right = cur;
else head = cur;
cur->left = pre;
pre = cur;
inorder(cur->right);
}
Node* treeToDoublyList(Node* root) {
if (root == NULL) return NULL;
inorder(root);
// 连接首尾节点
head->left = pre;
pre->right = head;
return head;
}
};
剑指 Offer 37. 序列化二叉树

用链表保存节点字符串
class Codec {
public:
void rserialize(TreeNode* root, string& str) {
if (root == nullptr) {
str += "None,";
} else {
str += to_string(root->val) + ",";
rserialize(root->left, str);
rserialize(root->right, str);
}
}
string serialize(TreeNode* root) {
string ret;
rserialize(root, ret);
return ret;
}
TreeNode* rdeserialize(list<string>& dataArray) {
if (dataArray.front() == "None") {
dataArray.erase(dataArray.begin());
return nullptr;
}
TreeNode* root = new TreeNode(stoi(dataArray.front()));
dataArray.erase(dataArray.begin());
root->left = rdeserialize(dataArray);
root->right = rdeserialize(dataArray);
return root;
}
TreeNode* deserialize(string data) {
list<string> dataArray;
string str;
for (auto& ch : data) {
if (ch == ',') {
dataArray.push_back(str);
str.clear();
} else {
str.push_back(ch);
}
}
if (!str.empty()) {
dataArray.push_back(str);
str.clear();
}
return rdeserialize(dataArray);
}
};
用vector
class Codec {
public:
int index;
void preorder(TreeNode* root, string& s) {
if (root == NULL) {
s += "$,";
return;
}
s += to_string(root->val) + ",";
preorder(root->left, s);
preorder(root->right, s);
}
// Encodes a tree to a single string.
string serialize(TreeNode* root) {
string s;
preorder(root, s);
return s;
}
// Decodes your encoded data to tree.
TreeNode* toTree(vector<string>& nodes) {
if (index >= nodes.size() || nodes[index] == "$") {
index++;
return NULL;
}
TreeNode* node = new TreeNode(stoi(nodes[index++]));
node->left = toTree(nodes);
node->right = toTree(nodes);
return node;
}
TreeNode* deserialize(string data) {
vector<string> nodes;
string str;
for (auto ch : data) {
if (ch == ',') {
nodes.push_back(str);
str.clear();
} else {
str.push_back(ch);
}
}
if (!str.empty()) {
nodes.push_back(str);
str.clear();
}
index = 0;
return toTree(nodes);
}
};
剑指 Offer 54. 二叉搜索树的第k大节点
二叉搜索树左中右遍历顺序得到的序列时升序,右中左得到的时降序,那么采取右中左的遍历方式,没访问一个节点,计数器-1,初始计数器为k,当计数器为0时,得到的就是第k大的节点
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int res;
int index;
void inorder(TreeNode* node) {
if (node == NULL) return;
inorder(node->right);
if (index == 0) return; // 剪枝
index--;
if (index == 0) {
res = node->val;
}
inorder(node->left);
}
int kthLargest(TreeNode* root, int k) {
index = k;
inorder(root);
return res;
}
};
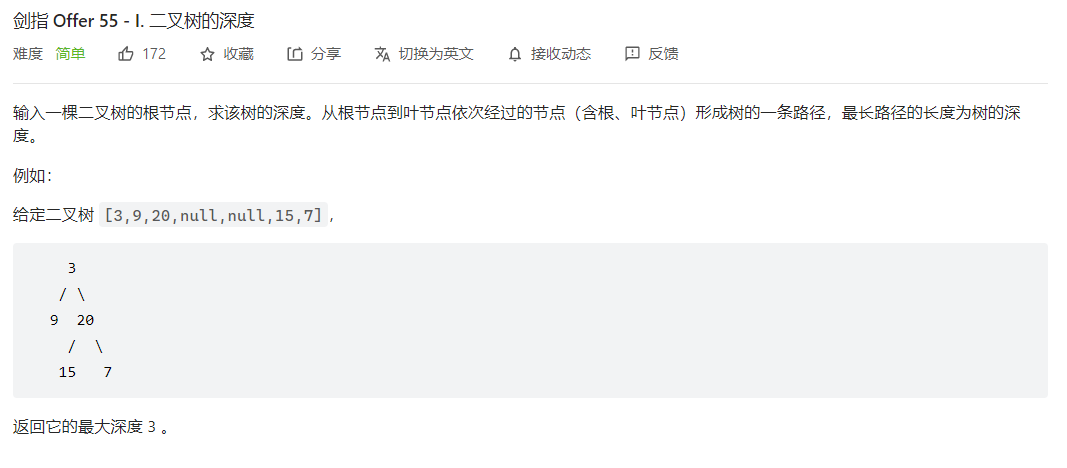
剑指 Offer 55 - I. 二叉树的深度
递归
class Solution {
public:
int maxDepth(TreeNode* root) {
if (root == NULL) return 0;
return max(maxDepth(root->left), maxDepth(root->right)) + 1;
}
};
层序遍历
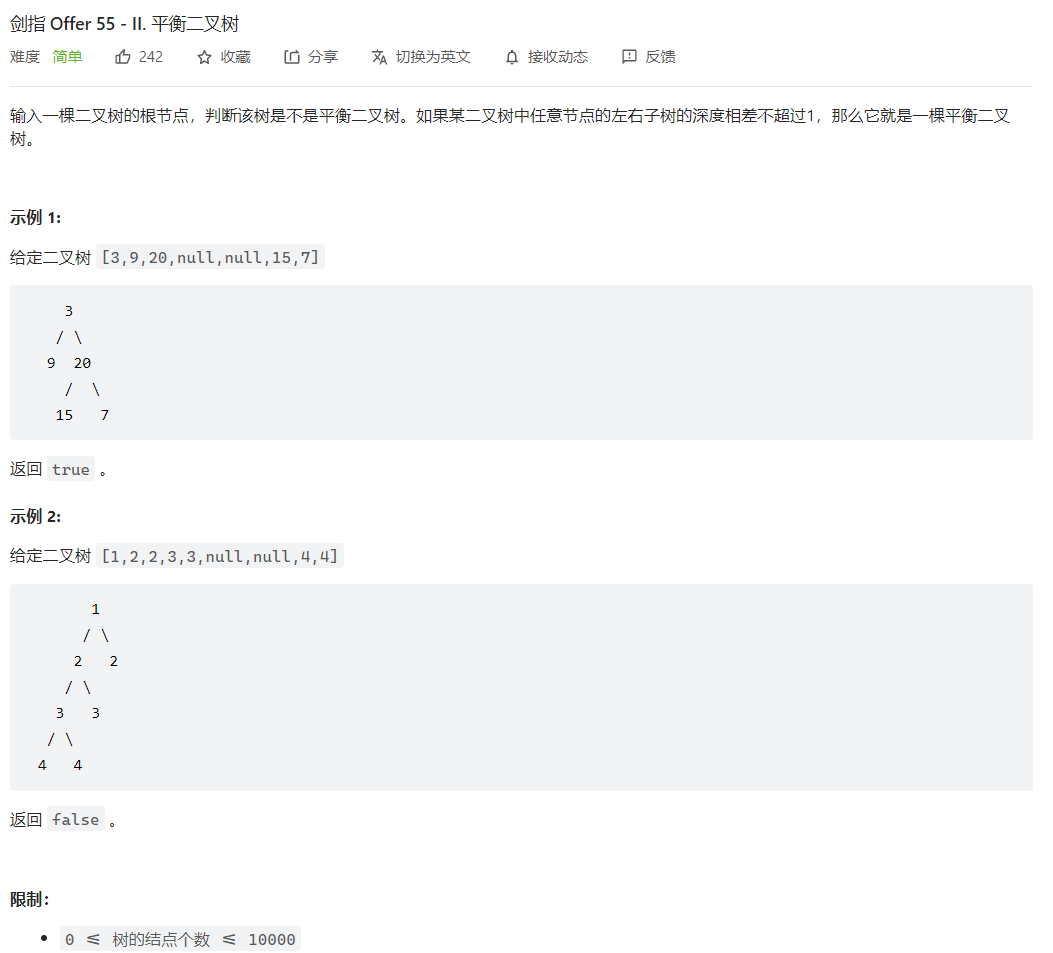
剑指 Offer 55 - II. 平衡二叉树
自底向上递归
class Solution {
public:
int dfs(TreeNode* root) {
if (root == NULL) return 0;
int left = dfs(root->left);
int right = dfs(root->right);
if (left == -1 || right == -1 || abs(left - right) > 1)
return -1;
return max(left, right) + 1;
}
bool isBalanced(TreeNode* root) {
return dfs(root) == -1 ? false : true;
}
};
自顶向下递归
可以分别求每个节点的深度,然后计算,复杂度较高
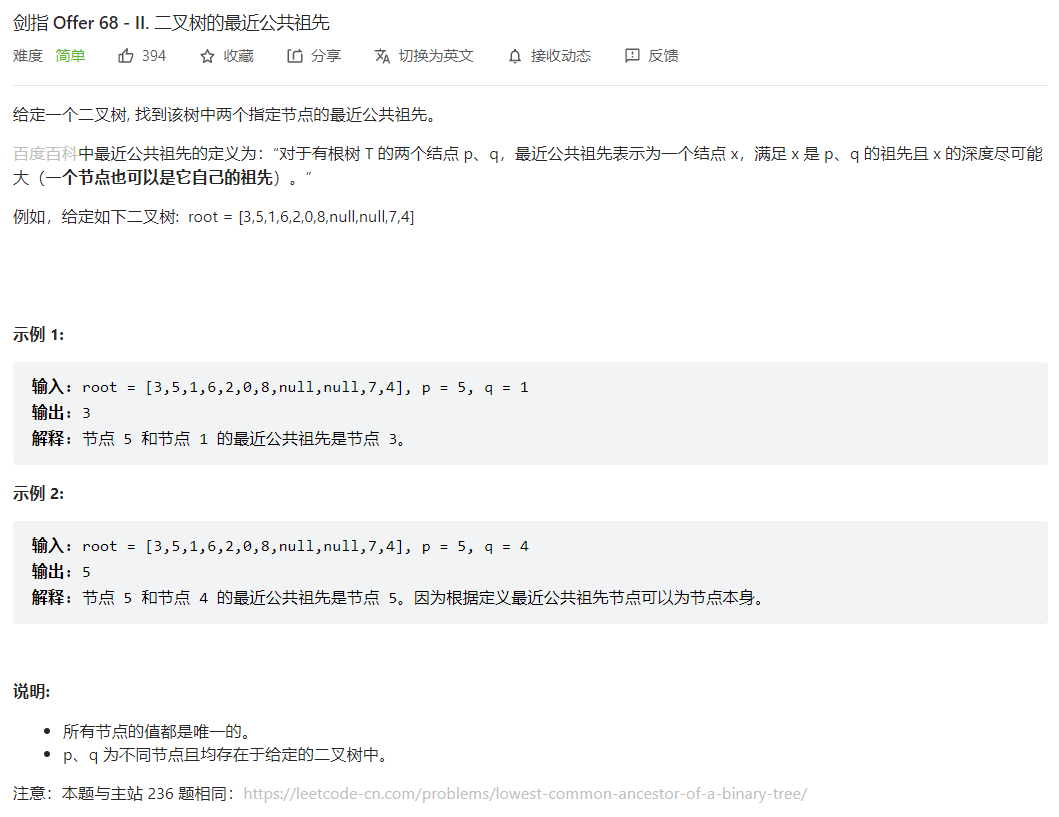
剑指 Offer 68 - I. 二叉搜索树的最近公共祖先
剑指 Offer 68 - II. 二叉树的最近公共祖先