如果在某个有序的集合（比如有序的数组、1 ~ n）里查找一些东西可以使用二分查找

写二分法，区间的定义一般为两种，左闭右闭即[left, right]，或者左闭右开即[left, right)。

704. 二分查找

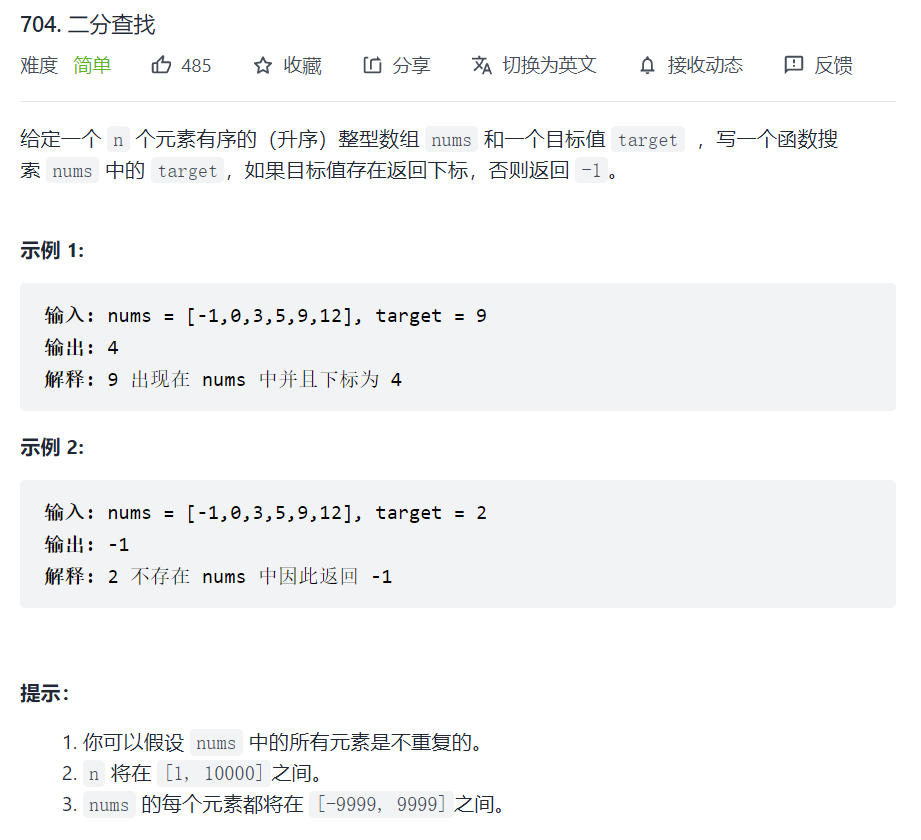
第一种写法 ：
[left, right] 左闭右闭区间，这使 left == right 有意义，因此 while 循环中的条件应该为
left <= right, 而当 nums[mid] != target 的时候，因为区间是右闭合的，所以下次搜索的范围应该为
[left, mid - 1]，因此赋值操作为 right = mid - 1

// 版本一
class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1; // 定义target在左闭右闭的区间里，[left, right]
        while (left <= right) { // 当left==right，区间[left, right]依然有效，所以用 <=
            int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
            if (nums[middle] > target) {
                right = middle - 1; // target 在左区间，所以[left, middle - 1]
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，所以[middle + 1, right]
            } else { // nums[middle] == target
                return middle; // 数组中找到目标值，直接返回下标
            }
        }
        // 未找到目标值
        return -1;
    }
};

第二种写法：
[left, right) 左闭右开区间，这时 left == right 没有意义，因此 while 循环中的条件应该为
left < right, 而当 nums[mid] != target 的时候，因为区间是右闭合的，所以下次搜索的范围应该为
[left, mid)，因此赋值操作为 right = mid

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size(); // 定义target在左闭右开的区间里，即：[left, right)
        while (left < right) { // 因为left == right的时候，在[left, right)是无效的空间，所以使用 <
            int middle = left + ((right - left) >> 1);
            if (nums[middle] > target) {
                right = middle; // target 在左区间，在[left, middle)中
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，在[middle + 1, right)中
            } else { // nums[middle] == target
                return middle; // 数组中找到目标值，直接返回下标
            }
        }
        // 未找到目标值
        return -1;
    }
};

35. 搜索插入位置

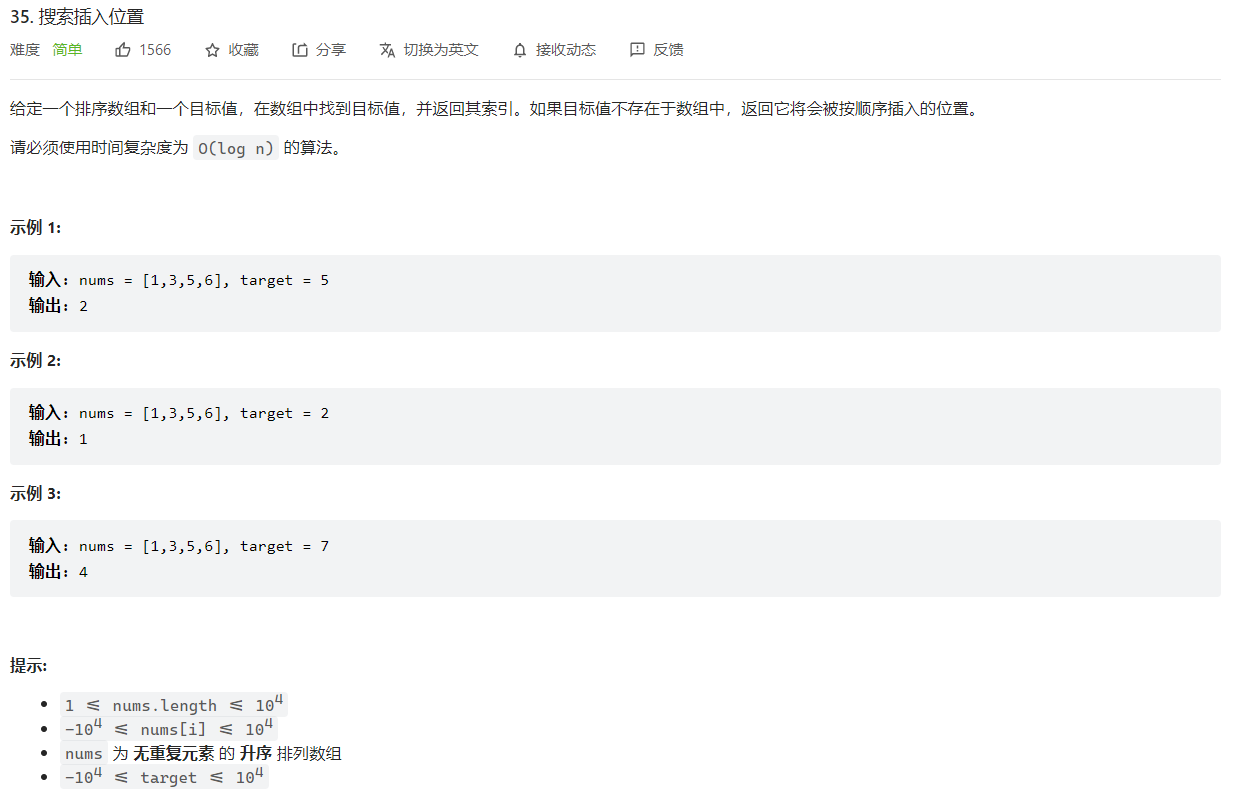
反思：这道题虽然简单，题目中的数组也是无重复元素的有序数组，并要求时间复杂度为O(logn)，那么很容易想到这道题要使用二分查找法，但是依然没有通过。这是因为我在解题的时候没有真正get到题目的点，也没有考虑如何处理边界问题。

再看题目要求，如果在数组中找到对应的元素，那么我们应该返回元素的索引，如果没有找到的话，要返回元素应该插入的位置，保持数组有序。在写代码之前应该考虑清楚在查找过程中可能出现的情况：
1. target比所有元素都小，插入数组头部
2. target已经存在于数组中
3. target插入数组中的某个位置
4. target比所有元素大，插入数组尾部
那么可以根据这四种情况来进行解题。

暴力解法

class Solution { 
    public:     
    int searchInsert(vector<int>& nums, int target) {         
        for (int i = 0; i < nums.size(); i++) {         
            // 分别处理如下三种情况         
            // 目标值在数组所有元素之前         
            // 目标值等于数组中某一个元素        
            // 目标值插入数组中的位置             
            if (nums[i] >= target) { // 一旦发现大于或者等于target的num[i]，那么i就是我们要的结果                 
                return i;             
            }         
        }         
        // 目标值在数组所有元素之后的情况         
        return nums.size(); // 如果target是最大的，或者 nums为空，则返回nums的长度     
    } 
};

二分查找

[left, right]左闭右闭的情况
依然讨论四种情况：
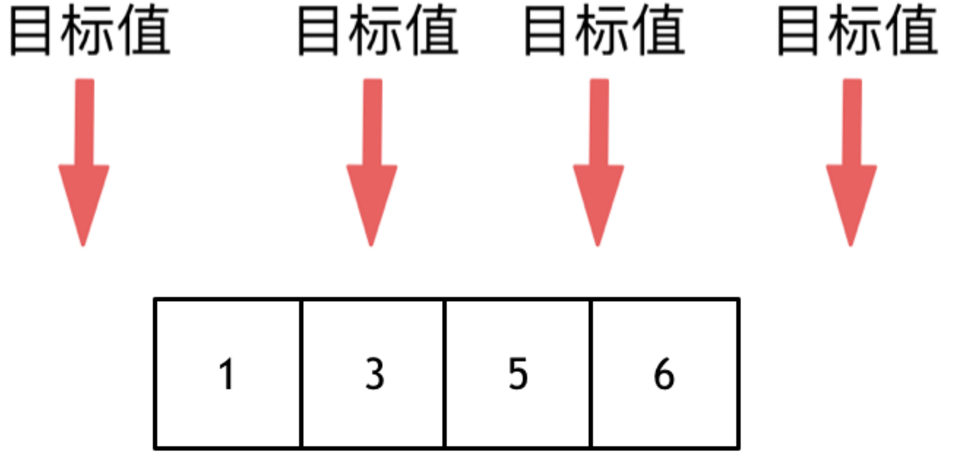
1. 如果target比所有元素都小，left始终指向第一个元素，right最后指向-1，第一个元素0，也就是right + 1就是要插入元素的位置
2. 如果target在数组中，那么直接在二分查找的循环中返回即可
3. 如果target应该插入数组中间的某个位置，在二分查找循环结束时，一定有left = mid = right，

• 如果target比三指针指向的元素小，target应该插入到后一个位置，因此返回right + 1
• 如果target比三指针指向的元素大，当前位置就是插入位置，但是会执行一次right - 1，因此返回right + 1

1. 如果target比所有元素都大，那么right始终指向最后一个元素，直到 left = right + 1，那么最一个元素之后的位置，right + 1就是要插入的位置，返回right+1

综上所述：

• target在数组中，返回其下标
• target不在数组中，返回right+1

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int left = 0, right = nums.size() - 1;
        while(left <= right) {
            int mid = left + ((right - left) >> 1);
            if (nums[mid] > target) {
                right = mid - 1;
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else {
                return mid;// target在数组中
            }
        }
        return right + 1;
    }
};

[left, right)左闭右开的情况：
right初值为n
while循环条件为left < right
target不在数组中时，只需要返回right即可

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int n = nums.size();
        int left = 0;
        int right = n; // 定义target在左闭右开的区间里，[left, right)  target
        while (left < right) { // 因为left == right的时候，在[left, right)是无效的空间
            int middle = left + ((right - left) >> 1);
            if (nums[middle] > target) {
                right = middle; // target 在左区间，在[left, middle)中
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，在 [middle+1, right)中
            } else { // nums[middle] == target
                return middle; // 数组中找到目标值的情况，直接返回下标
            }
        }
        // 分别处理如下四种情况
        // 目标值在数组所有元素之前 [0,0)
        // 目标值等于数组中某一个元素 return middle
        // 目标值插入数组中的位置 [left, right) ，return right 即可
        // 目标值在数组所有元素之后的情况 [left, right)，return right 即可
        return right;
    }
};

二分查找查找数组某元素上下边界

对于二分查找，如果是查找某一元素是否在数组中，如果存在则返回数组下标，需要满足一个条件是数组中的元素不能有重复，因为有重复元素查找后返回的下标不确定，但是如果数组中有重复元素并且有序的话，可以利用二分查找来寻找某个元素的边界，即这个元素第一次出现的位置和最后一次出现的位置。

在下面的讨论中，二分查找使用的都是[left, right]左闭右闭区间
首先，寻找上界。
寻找第一个大于target的元素，当 nums[mid] <= target时，要在mid右边继续查找，如果nums[mid] > target，要在mid左边继续查找。查找时可能会出现的几种情况：

• target不存在并且target比所有元素都要小，right一直左移直到right = -1，最终left = 0 为第一个大于target的元素，比如在下面的数组中寻找1，因为1不存在，所以最后一次循环left、mid、right指向索引为0的元素，因为 3 > 1，所以 right = mid - 1 = -1，而 left = 1，此时left指向的元素就是第一个大于target的元素
  
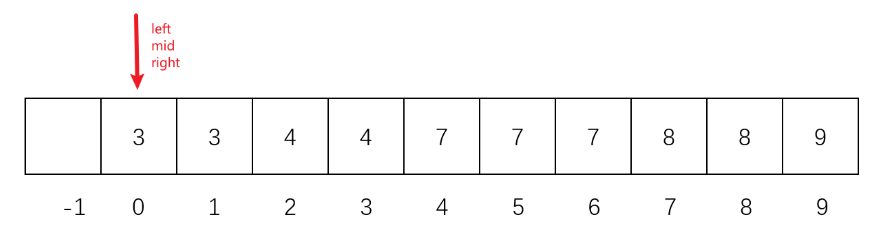
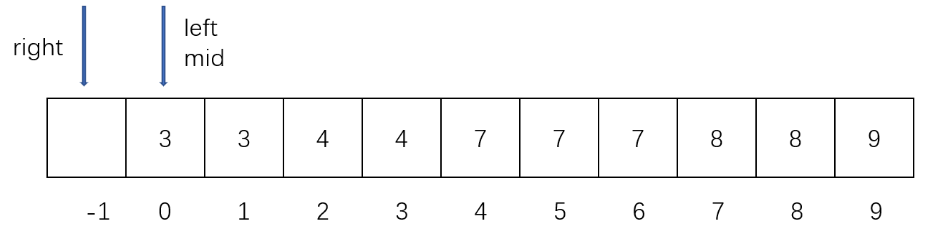
• target在数组中，比如查找3的上界，最后一次循环left、mid、right指向索引为2的元素，因为 4 > 3，所以 right = mid - 1 = 1，而 left = 2，此时left指向的元素就是第一个大于target的元素

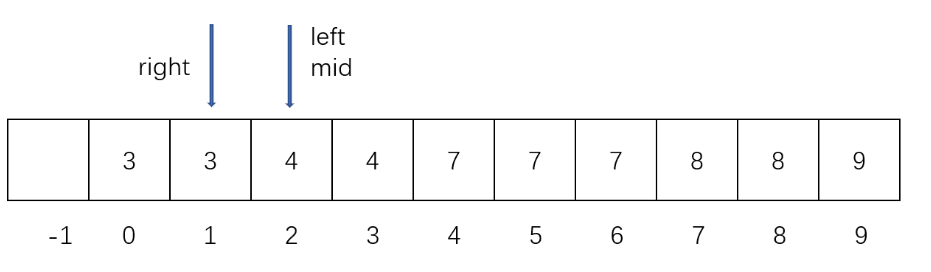
• target在数组中，比如查找9的上界，最后一次循环left、mid、right指向索引为9的元素，因为 9 <= 9，所以 left = mid + 1 = 10，这代表比target大的元素不存在，此时left指向的元素就是第一个大于target的元素（下标越界，表示不存在）

综上所述，循环结束后left就是上界

int upper_bound1(vector<int> nums, int target) {
    int n = nums.size();
    int left = 0, right = n - 1;
    while (left <= right) {
        int mid = left + ((right - left) >> 1);
        if (nums[mid] <= target) {
            left = mid + 1;
        } else {
            right = mid - 1;
        }
    }
    return left;
}

寻找下界，和寻找上界类似，返回right

// 用二分查找找第一个小于target的元素
int lower_bound1(vector<int> nums, int target) {
    int n = nums.size();
    int left = 0, right = n - 1;
    while (left <= right) {
        int mid = left + ((right - left) >> 1);
        if (nums[mid] >= target) {
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }
    return right;
}

34. 在排序数组中查找元素的第一个和最后一个位置

这个题依然是有序数组，但是这道题不同的是有重复元素
暴力解法：
遍历数组，当找到第一个值为target的元素时，记录target出现的开始位置，然后用一个指针去继续往下搜索，直到找到第一个不为target的元素为止，时间复杂度为O(nm)

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        int n = nums.size();
        for (int i = 0; i < n; ++i) {
            if (target == nums[i]) {
                int r = i;
                while(r < n && nums[r] == target) r++;//找到结束位置的后一个位置
                return vector<int>{i, r - 1};
            }
        }
       return vector<int>{-1, -1};    
    }
};

二分查找：
二分查找遇到有重复元素的有序数组时，会出现返回的索引位置不确定的情况，但是对于这道题来说，要找一个范围，那么可以用二分查找找到某一个target元素，然后用两个指针来寻找左区间和右区间

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        int n = nums.size();
        int left = 0, right = n - 1;
        while(left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] > target) {
                right = mid - 1;
            } else if (nums[mid] < target){
                left = mid + 1;
            } else {
                int l = mid, r = mid;
                while(l >= 0 && nums[l] == target) l--; //寻找左区间
                while(r < n && nums[r] == target) r++; //寻找右区间

                return vector<int>{l + 1, r - 1};
            }
        }
        return vector<int>{-1, -1}; 
    }
};

二分查找的另一个思路：
用二分查找找到第一个小于target的元素位置和第一个大于target的元素位置
返回他俩中间的部分

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        if(nums.empty()) return {-1,-1};

        int l = 0, r = nums.size() - 1; //二分范围
        while( l < r)                   //查找元素的开始位置
        {
            int mid = (l + r )/2;
            if(nums[mid] >= target) r = mid;
            else l = mid + 1;
        }
        if( nums[r] != target) return {-1,-1};  //查找失败
        int L = r;
        l = 0, r = nums.size() - 1;     //二分范围
        while( l < r)                   //查找元素的结束位置
        {
            int mid = (l + r + 1)/2;
            if(nums[mid] <= target ) l = mid;
            else r = mid - 1;
        }
        return {L,r};
    }
};

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        if (nums.size() == 0) return {-1, -1};
        int left = 0, right = nums.size() - 1;
        // 查找元素开始位置
        while (left <= right) {
            int mid = left + ((right - left) >> 1);
            if (nums[mid] >= target) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        // 注意数组下标越界问题
        // 如果right始终没有动过，说明数组元素都比target小
        // 如果nums[right + 1] != target, 那么说明target不存在
        if( right + 1 == nums.size() || nums[right + 1] != target) 
            return {-1,-1}; 
        int L = right + 1; //起始位置

        left = 0, right = nums.size() - 1;
        while (left <= right) {
            int mid = left + ((right - left) >> 1);
            if (nums[mid] <= target) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        return {L, left - 1};
    }
};

使用STL：
STL永远滴神：
先用lower_bound找下界(闭区间)
如果元素不存在(下界超出数组范围或者第一个不小于target的元素不是target)直接返回{-1,-1}，
如果元素存在再用upper_bound寻找上界(开区间，所以要减1)，
最后返回上下界就ok了。

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        if(nums.empty()) return {-1,-1};
        int lower = lower_bound(nums.begin(), nums.end(), target) - nums.begin();
        if (lower == nums.size() || nums[lower] != target)
            return {-1, -1};
        int upper = upper_bound(nums.begin(), nums.end(), target) - nums.begin();
        return {lower, upper - 1};
    }
};

240. 搜索二维矩阵 II

思路一：暴力（超时）

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        for (auto arr : matrix) {
            for (auto num : arr) {
                if (num == target)
                    return true;
            }
        }
        return false;
    }
};

暴力解法没有用到矩阵的特性：

• 每行的元素从左到右升序排列。
• 每列的元素从上到下升序排列。

时间复杂度为O(mn)，空间复杂度为O(1)，提交后显示超时

思路二：二分查找

因为矩阵“有序”的特性，可以对每一行进行二分查找

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        for (const auto& arr : matrix) {
            auto it = lower_bound(arr.begin(), arr.end(), target); // 二分查找
            if (it != arr.end() && *it == target)
                return true;
        }
        return false;
    }
};

• 时间复杂度为O(mlogn)。对每一行使用二分查找的时间复杂度为O(logn)，最多需要进行m次二分查找
• 空间复杂度O(1)

通过提交结果发现，这种算法也不是特别快

思路三：从右上角开始搜索

从矩阵的右上角开始搜索，假设当前位置的坐标为（x, y），x的范围为[0, m-1]，y的范围为[0, n-]:

• 假如matrix[x][y] > taeget，由于矩阵在行上升序，另y-1
• 假如matrix[x][y] < taeget，由于矩阵在列上升序，另x+1
• matrix[x][y] = taeget，返回true
• 如果超出范围，则返回false

代码如下：

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m = matrix.size(), n = matrix[0].size();
        int x = 0, y = n - 1;
        while (x < m && y >= 0) {
            if (matrix[x][y] > target) y--;
            else if (matrix[x][y] < target) x++;
            else return true;
        }
        return false;
    }
};

可以看到时间快了很多

367. 有效的完全平方数

首先想到的是暴力解题，直接遍历 1 ~ num - 1，简化一点遍历 1 ~ （num/2）
但是会超时，因此考虑其他解法, 这道题其实可以理解为在 1 ~ num 里找到一个数，使其平方等于num，如果找到了的话，返回true，否则返回false，那么1~num显然是有序的并且无重复元素，那么可以使用二分查找来降低时间复杂度

class Solution {
public:
    bool isPerfectSquare(int num) {
        if (num < 2) return true;
        long left = 2, right = num / 2, square; // 用long是为了防止溢出
        while (left <= right) {
            long mid = left + ((right - left) >> 1);
            long square = mid * mid;
            if (square > num) {
                right = mid - 1;
            } else if (square < num) {
                left = mid + 1;
            } else {
                return true;
            }
        }
        return false;
    }
};

69. Sqrt(x)

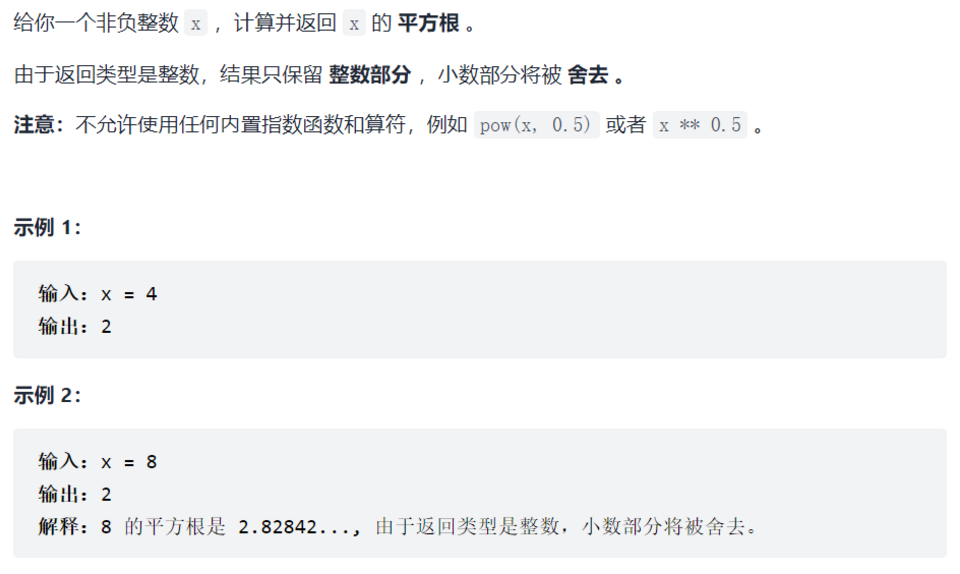
这题可以理解为在 1 ~ x 内查找第一个不小于 sqrt(x) 的数，用二分查找即可解决，类似于找有重复的有序数组某一元素的上界

class Solution {
public:
    int mySqrt(int x) {
        int left = 1, right = x;
        // 在 1 ~ x 范围内寻找第一个大于sqrt(x)的元素
        while (left <= right) {
            int mid = left + ((right - left) >> 1);
            long long square = mid * mid;
            if (square <= x) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        return left - 1;
    }
};

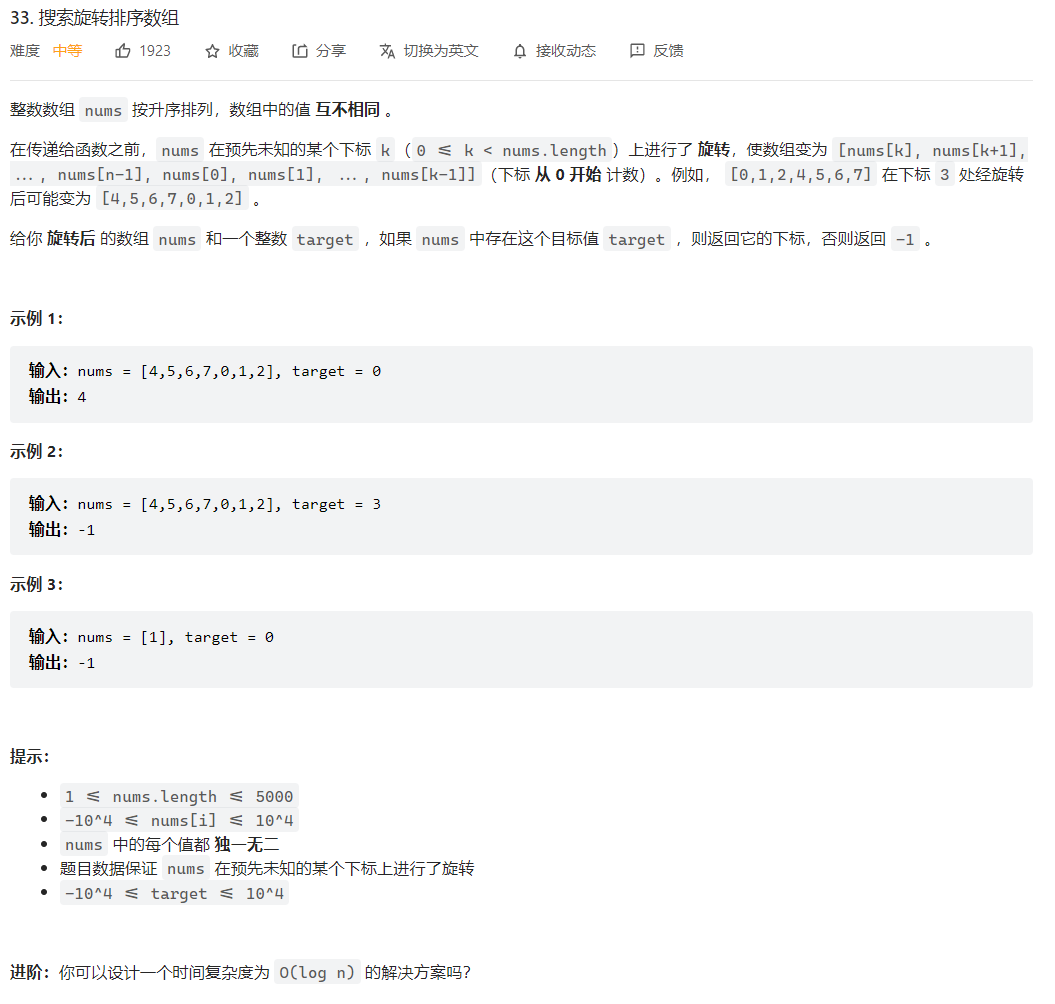
33. 搜索旋转排序数组

有序数组的查找可以使用二分查找
有序数组旋转后，用mid将数组一分为二，一定会有一半数组是有序的，如果target在有序的那一半中，那么移动边界，在有序的一半中继续查找，否则，在另一半查找

ps: 这道题直接套用二分模板不太好，不容易将区间划分为左右两部分，因此按照两边的区间是否有序进行讨论

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int l = 0, r = nums.size() - 1;
        while (l <= r) {
            int mid = (l + r) >> 1;
            if (nums[mid] == target) return mid;
            else if (nums[mid] >= nums[l]) { // 左边区间是有序的
                if (nums[mid] > target && nums[l] <= target) r = mid - 1;
                else l = mid + 1;
            } else { // 右边区间是有序的
                if (nums[mid] < target && nums[r] >= target) l = mid + 1;
                else r = mid - 1;
            }
        }
        return -1;
    }
};

81. 搜索旋转排序数组 II

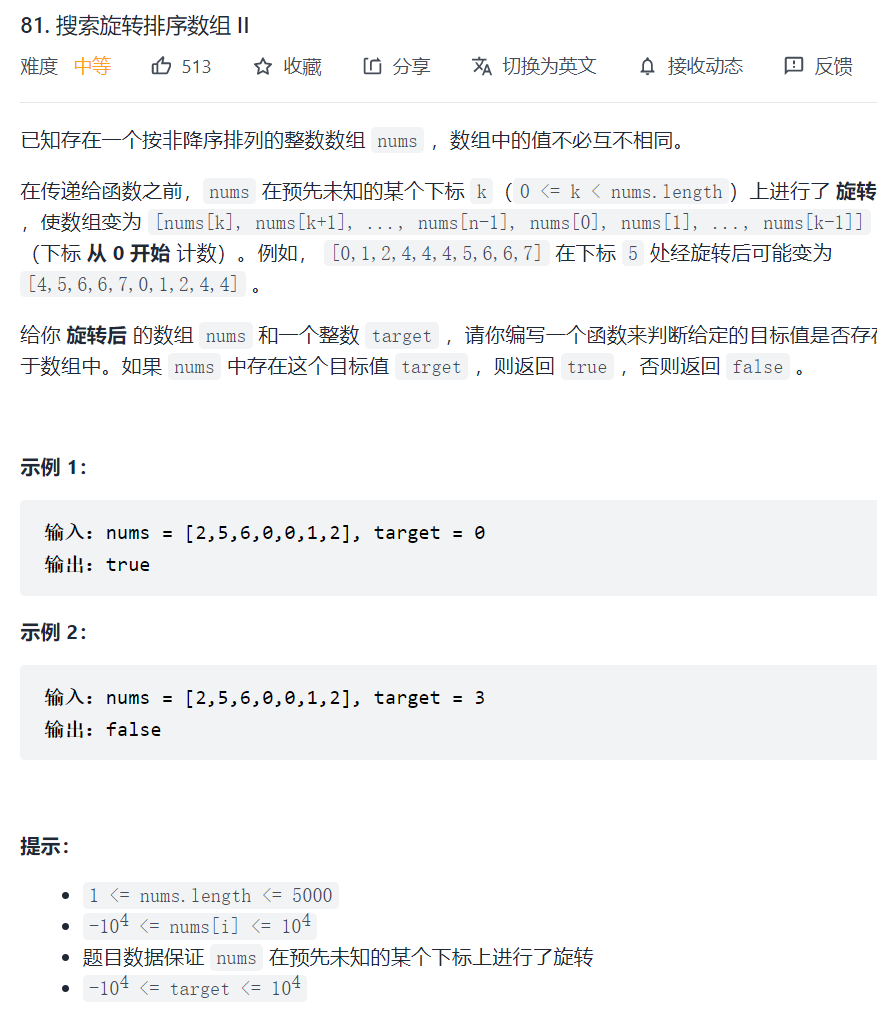
33题的序列是严格递增的，这一题有重复数字

修改33题的代码，增加限制条件即可

class Solution {
public:
    bool search(vector<int>& nums, int target) {
        int l = 0, r = nums.size() - 1;
        while (l <= r) {
            int mid = (l + r) >> 1;
            if (nums[mid] == target) return true;
            // 中间值和左右端点有一样，无法判断哪边有序，收缩一下区间范围
            if (nums[mid] == nums[l] && nums[mid] == nums[r]) {
                l++;
                r--;
            } else if (nums[mid] >= nums[l]) {
                if (nums[mid] > target && nums[l] <= target) r = mid - 1;
                else l = mid + 1;
            } else {
                if (nums[mid] < target && nums[r] >= target) l = mid + 1;
                else r = mid - 1;
            }
        }
        return false;
    }
};

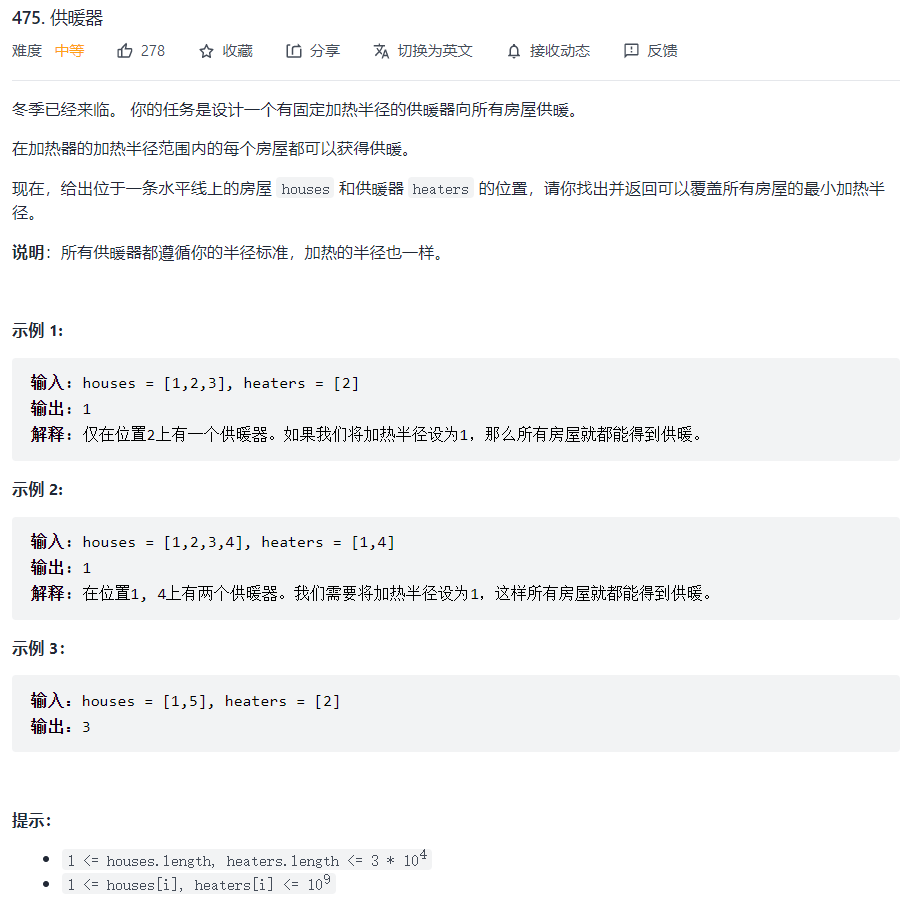
(每日一题)475. 供暖器💦

思路一：排序+二分查找

对于每一个房屋，选择距离该房屋最近的供暖器，最近的供暖器就是要覆盖的最小半径，所有房屋需要供暖器最小半径的最大值就是要求的结果

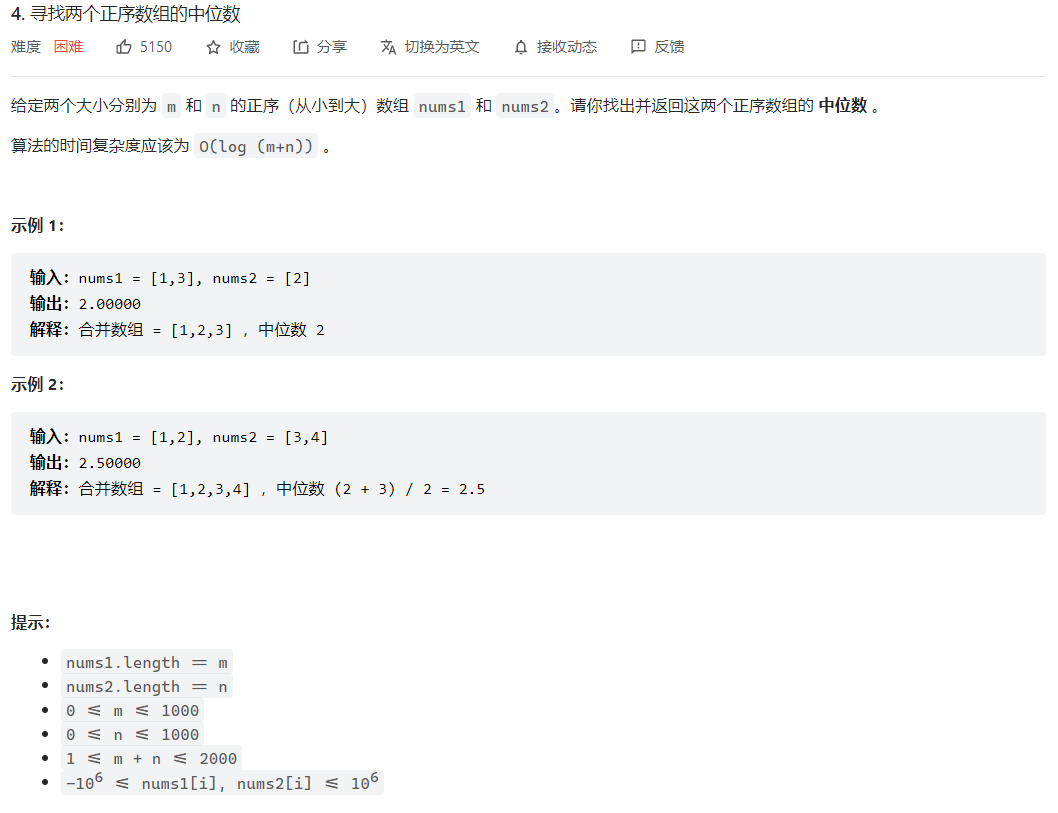
4. 寻找两个正序数组的中位数💦

O(M + N)

归并排序的思想，但是时间复杂度不满足题目要求

使用辅助数组

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        vector<int> arr;
        int m = nums1.size(), n = nums2.size();
        int i = 0, j = 0;
        while (i < m && j < n) {
            if (nums1[i] < nums2[j]) {
                arr.push_back(nums1[i++]);
            } else {
                arr.push_back(nums2[j++]);
            }
        }

        while (i < m) arr.push_back(nums1[i++]);
        while (j < n) arr.push_back(nums2[j++]);

        int len = m + n;
        if (len % 2) return arr[len / 2];
        else return (arr[(len - 1) / 2] + arr[(len + 1) / 2]) / 2.0;      
    }
};

时间复杂度为O(M + N)
空间复杂度为O(M + N)

不使用辅助数组

因为两个数组长度是固定的，因此可以维护两个指针，来记录扫描了多少元素，不需要将元素都存放到辅助数组，找到中位数对应的下标即可
但是这样时间复杂度也为O(M + N)

题目要求复杂度为O(log(M + N))，显然上述解法不符合要求，考虑到给的数组是有序的，因此尝试二分查找来解决问题

二分查找

官方题解
可以看作查找两个数组中第k小的数，将k一分为二，判断两个数组中的k/2位置的元素，假设nums1[k/2] > nums2[k/2]， 那么nums2中前一部分元素无论如何也不可能存在第k小的数，那么将其删除，从nums1[0 ~ n]和nums[k/2 + 1]中寻找第 k - k/2小的数，循环直到k等于1，取两个数组中的较小者即可

class Solution {
public:
    int getKth(vector<int>& nums1, vector<int>& nums2, int k) {
        int m = nums1.size(), n = nums2.size();
        int i = 0, j = 0; // 分别为两个数组的索引

        while (true) {
            // 边界条件
            // 如果有一个数组删完了，直接返回另一个数组第k小的元素
            if (i >= m) return nums2[j + k - 1];
            if (j >= n) return nums1[i + k - 1];
            // 如果k等于1，返回i，j指向的最小的那一个
            if (k == 1) return min(nums1[i], nums2[j]);

            int x = min(i + k / 2 - 1, m - 1), y = min(j + k / 2 - 1, n - 1);
            int a = nums1[x], b = nums2[y];
            if (a <= b) { // 删除第一个数组前一部分
                k -= x - i + 1;
                i = x + 1;
            } else { // 删除第二个数组前一部分
                k -= y - j + 1;
                j = y + 1;
            }
        }
    }

    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int len = nums1.size() + nums2.size();
        if (len & 1) { // 总长度是奇数，返回中间元素
            return getKth(nums1, nums2, (len + 1) >> 1);
        } else { // 总长度为偶数，返回中间两个元素的平均值
            return (getKth(nums1, nums2, len / 2) + getKth(nums1, nums2, len / 2 + 1)) / 2.0;
        }
    }
};

(2022.06.07每日一题)875. 爱吃香蕉的珂珂

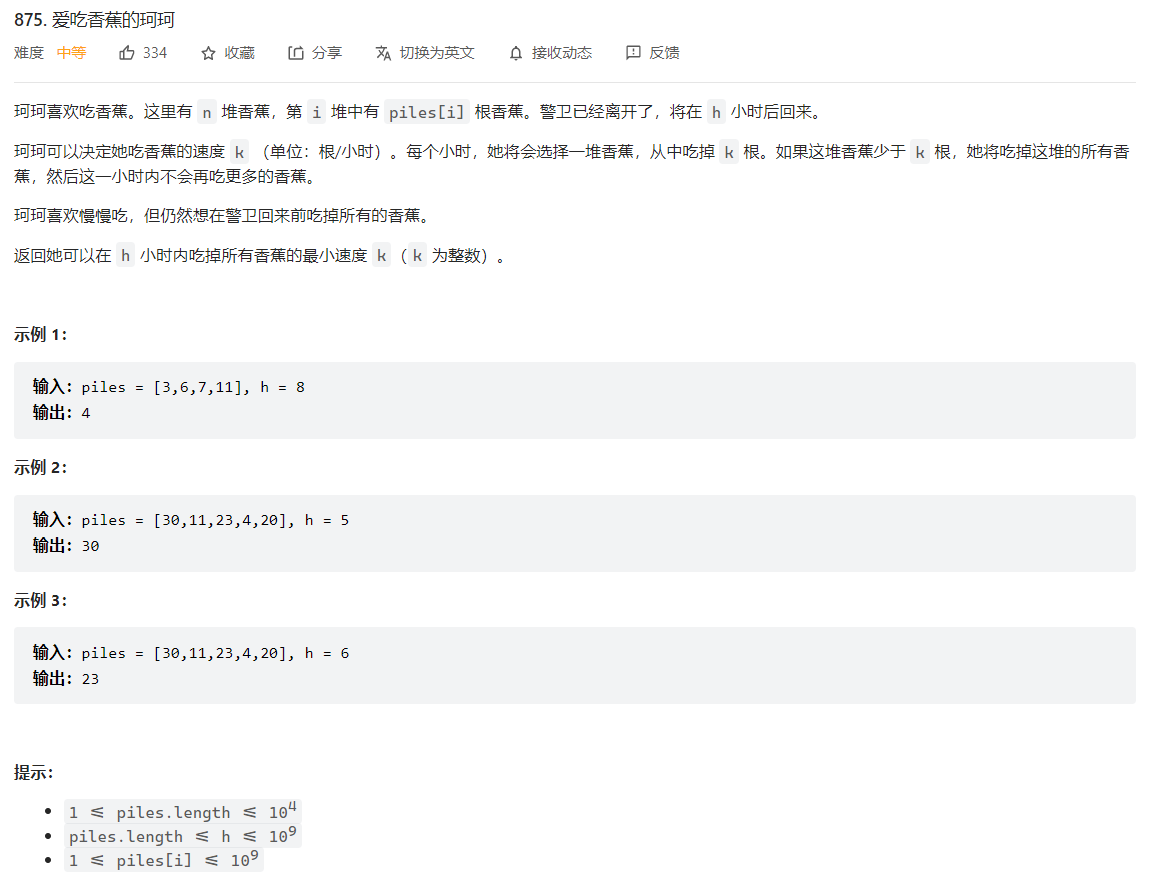
吃香蕉的速度最快为最多的那一堆香蕉的数量，此时用时最少，耗时为piles.size()
最慢的速度为1个，用时最多。
满足在h时间内吃完的最小速度一定在 1 - max(piles) 之间，可以使用二分查找。

设时间为speed，吃完每一堆香蕉所用时间为,对于每一个速度可以求得吃完所有香蕉的耗时，向上取整的实现方式为
套用二分查找模板：

class Solution {
public:
    bool check(vector<int>& piles, int h, int speed) {
        int times = 0;
        for (auto pile : piles) {
            int t = (pile + speed - 1) / speed;
            times += t;
        }
        return times <= h; // 如果总时间比h小，那么吃的可以再慢一点
    }
    int minEatingSpeed(vector<int>& piles, int h) {
        int l = 1, r = *max_element(piles.begin(), piles.end());
        while (l < r) {
            int mid = r + l >> 1;
            if (check(piles, h, mid)) r = mid;
            else l = mid + 1;
        }
        return r;
    }
};

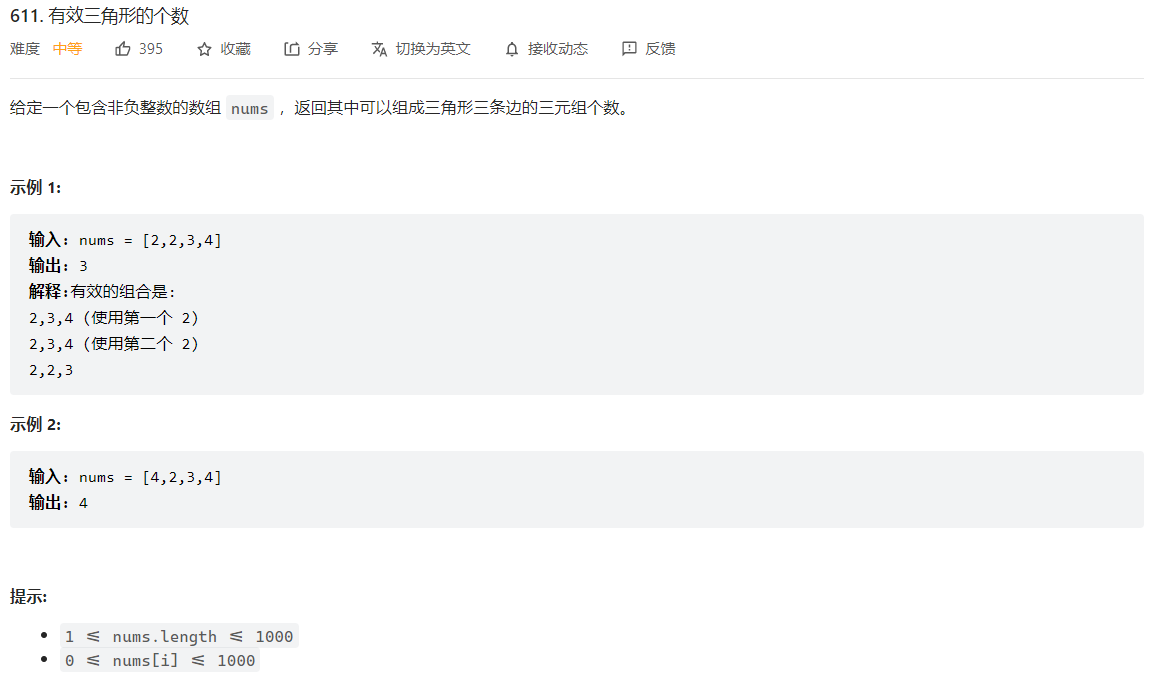
611. 有效三角形的个数

排序+二分

三个值a，b，c能够组成三角形的条件是 a + b > c 、 a + c > b 、b + c > a
对数组进行排序，从小到大枚举前两条边a，b，从大于b的数中查找第三条边c，这时候一定满足a + c > b 、b + c > a，只需查找a + b > c 的数值即可

class Solution {
public:
    int triangleNumber(vector<int>& nums) {
        if (nums.size() < 3) return 0;

        sort(nums.begin(), nums.end());

        int res = 0;
        for (int i = 0; i < nums.size(); i++) { // a
            for (int j = i + 1; j < nums.size(); j++) { // b
                int l = j + 1, r = nums.size() - 1;
                while (l < r) {
                    int mid = (l + r + 1) >> 1; // c
                    // 找到满足 a + b > c 的nums[mid]
                    if (nums[mid] < nums[i] + nums[j]) {
                        l = mid;
                    } else {
                        r = mid - 1;
                    }
                }
                if (nums[r] < nums[i] + nums[j])
                    res += r - j; // r 到 j范围内的所有数都满足 a + b > c
            }
        }
        return res;
    }
};

• 时间复杂度：排序O(NlogN)，遍历O(N^2logN)，总复杂度O(N^2logN)

排序+双指针

思路见注释

class Solution {
public:
    int triangleNumber(vector<int>& nums) {
        if (nums.size() < 3) return 0;

        sort(nums.begin(), nums.end());

        int res = 0;
        for (int i = 0; i < nums.size(); i++) { // a
            int k = i; // c
            // 随着j的增大 k也是增大，具有单调性， 可以使用双指针
            for (int j = i + 1; j < nums.size(); j++) { // b
                // 找到满足 a + b > c 的最大的c
                while (k + 1 < nums.size() && nums[k + 1] < nums[i] + nums[j]) k++;
                res += max(k - j, 0); // 如果不存在此k，那么 k - j是负数
            }
        }
        return res;
    }
};

• 时间复杂度O(N^2)

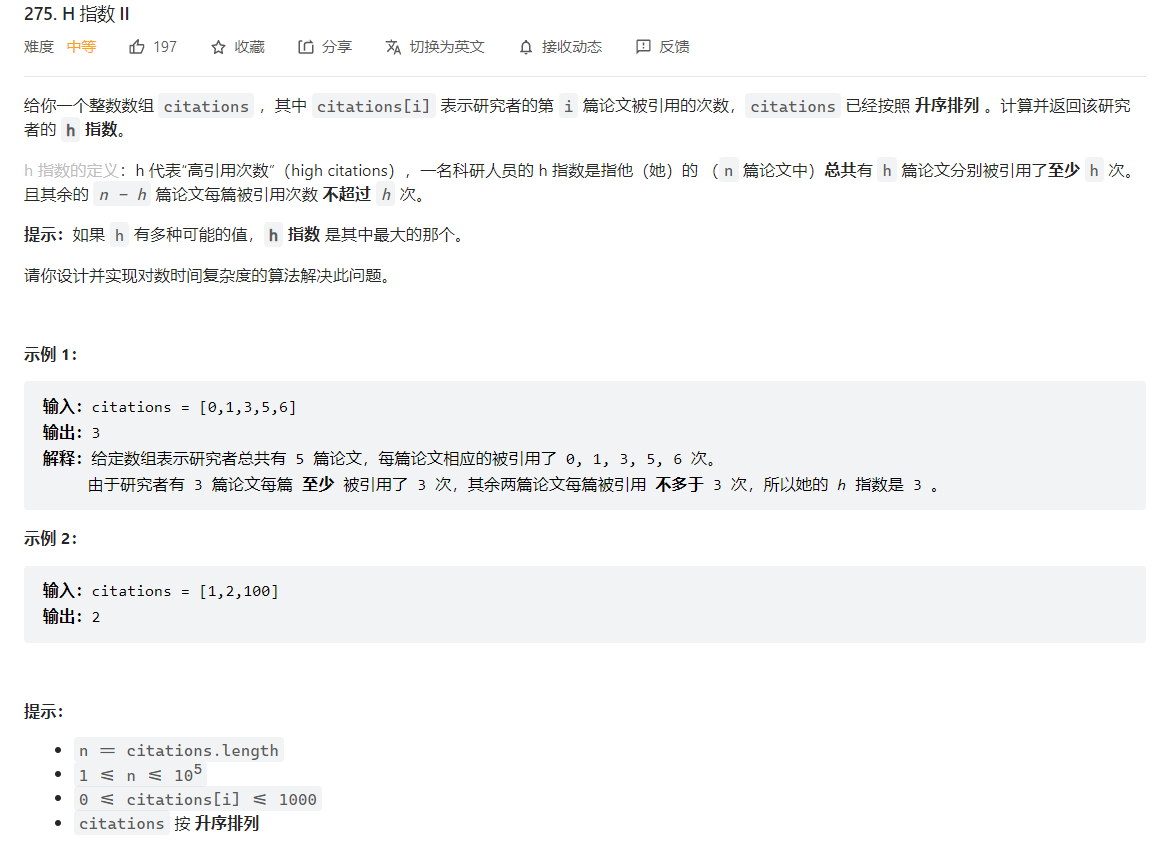
275. H 指数 II

迭代

给定的数组已经按照升序排序，h指数最大为数组的大小，可以从大到小枚举h指数，如果第h大的数满足 大于等于h，那么就找到了最大的h指数

class Solution {
public:
    int hIndex(vector<int>& citations) {
        int h = citations.size();
        for (int i = 0; i < citations.size(); i++) {
            if (citations[i] >= h) break;
            h--;
        }
        return h;
    }
};

• 时间复杂度O(N)

二分

给定的数组已经按照升序排序，h指数最大为数组的大小，最小为0，可以使用二分查找

class Solution {
public:
    int hIndex(vector<int>& citations) {
        int n = citations.size();
        int l = 0, r = n;
        while (l < r) {
            int mid = (l + r + 1) >> 1;
            // 如果这个mid满足条件，那么h指数可能会更大，因此搜索右区间
            if (citations[n - mid] >= mid) l = mid; 
            else r = mid - 1;
        }
        return r;
    }
};

1011. 在 D 天内送达包裹的能力

class Solution {
public:
    int shipWithinDays(vector<int>& weights, int days) {
        // 运载能力上界，将所有物品全部打成一包，一天都运过去，此时days = 1
        // 运载能力下界, 物品最大重量，有可能一天只运一件
        int l = *max_element(weights.begin(), weights.end());
        int r = accumulate(weights.begin(), weights.end(), 0);
        while (l < r) {
            int mid = (l + r) >> 1;
            int day = 1, weight = 0;
            for (auto w : weights) {
                if (weight + w > mid) {
                    day++;
                    weight = 0;
                }
                weight += w;
            }

            if (day <= days) r = mid; // 尝试更小的运载能力，搜索左半部分
            else l = mid + 1;
        }
        return r;
    }
};

• 时间复杂度O(log(sum(weights)))

1482. 制作 m 束花所需的最少天数

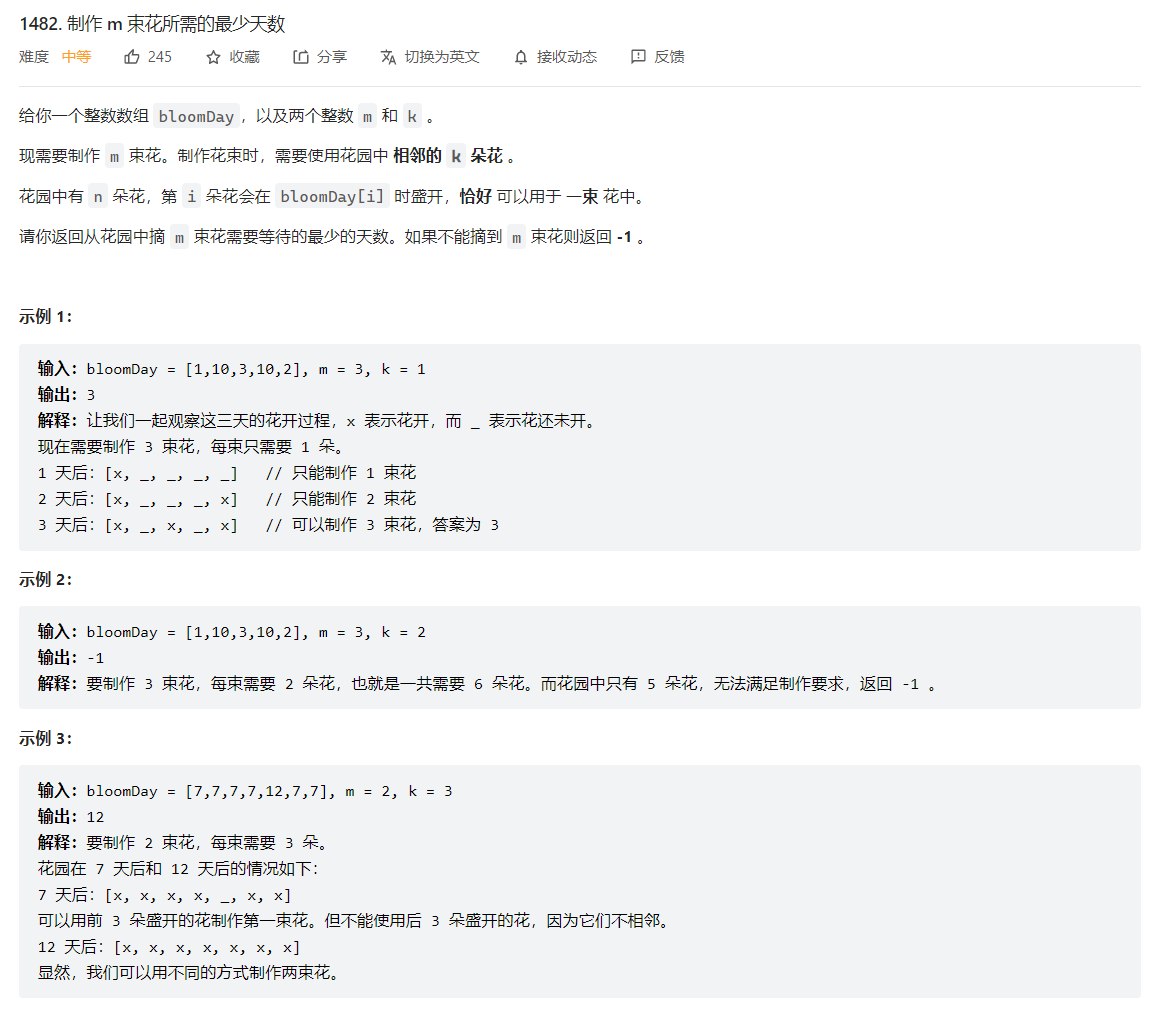
class Solution {
public:
    bool check(vector<int>& bloomDay, int m, int k, int x) {
        int num = 0; // 共能得到多少束花
        for (int i = 0; i < bloomDay.size(); i++) {
            int j = i;
            while (j < bloomDay.size() && bloomDay[j] <= x) j++;
            num += (j - i) / k;
            if (num >= m) return true;
            i = j;
        }
        return false;
    }

    int minDays(vector<int>& bloomDay, int m, int k) {
        // 花园中一共bloomDay朵花
        if (bloomDay.size() < m * k) return -1;
        // 最多等待max(bloomDay)天  最少等待min(bloomDay)天
        // 对于等待天数，看看是否存在m组连续的k个花
        int l = *min_element(bloomDay.begin(), bloomDay.end());
        int r = *max_element(bloomDay.begin(), bloomDay.end());
        while (l < r) {
            int mid = (l + r) >> 1;
            if (check(bloomDay, m, k, mid)) r = mid;
            else l = mid + 1;
        }
        if (check(bloomDay, m, k, r)) return r;
        return -1;
    }
};

• 时间复杂度O(n_log(_high−low))

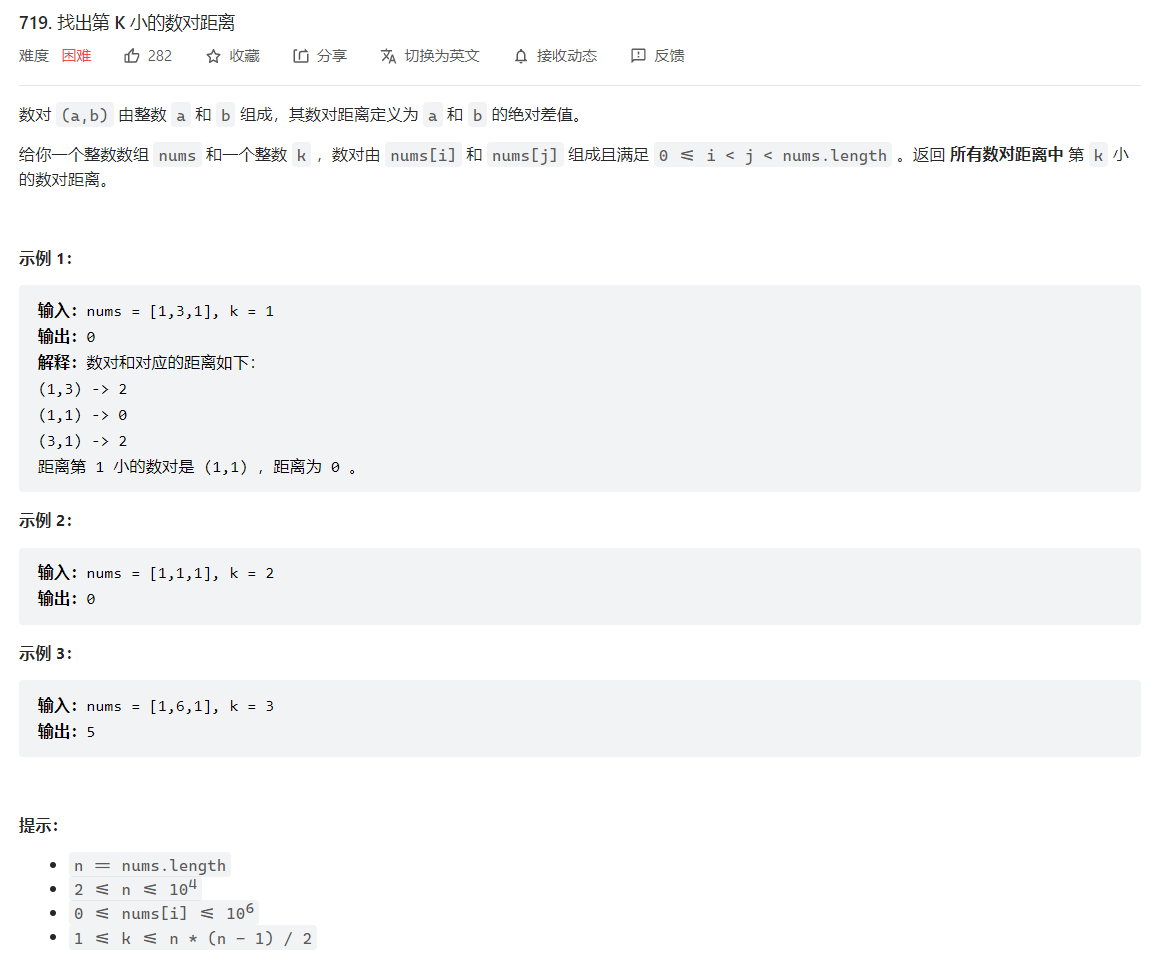
719. 找出第 K 小的数对距离

二分+二分

距离最小为0， 最大为max - min，可以二分查找第k小的数
二分查找算法的特性，最终找到的距离一定是数组中存在的
简单证明：假设最后找到的 r不存在，那么r最后代表的距离一定是第k小的数的左边界，如果这个边界比第k小的数大，那么还会继续搜索左边界，最后r一定指向在存在的第k小的距离

class Solution {
public:
    int smallestDistancePair(vector<int>& nums, int k) {
        int n = nums.size();
        sort(nums.begin(), nums.end());
        int l = 0, r = nums[0] + nums[n - 1];
        while (l < r) {
            int mid = (l + r) >> 1;
            int cnt = 0;
            // 统计比mid小的距离有多少个
            for (int j = 0; j < n; j++) {
                int ll = 0, rr = j;
                while (ll < rr) {
                    int mm = (ll + rr) >> 1;
                    if (nums[j] - nums[mm] <= mid) rr = mm;
                    else ll = mm + 1;
                }
                cnt += j - rr; // 以j为右端点的不超过mid的距离数累加
            }
            if (cnt >= k) r = mid;
            else l = mid + 1;
        }
        return r;
    }
};

二分+双指针

统计比mid小的数可用双指针来优化

class Solution {
public:
    int smallestDistancePair(vector<int>& nums, int k) {
        int n = nums.size();
        sort(nums.begin(), nums.end());
        int l = 0, r = nums[n - 1] - nums[0];
        while (l < r) {
            int mid = (l + r) >> 1;
            int cnt = 0;
            for (int i = 0, j = 0; j < n; j++) {
                while (nums[j] - nums[i] > mid) i++;
                cnt += j - i;
            }
            if (cnt >= k) r = mid;
            else l = mid + 1;
        }
        return r; 
    }
};