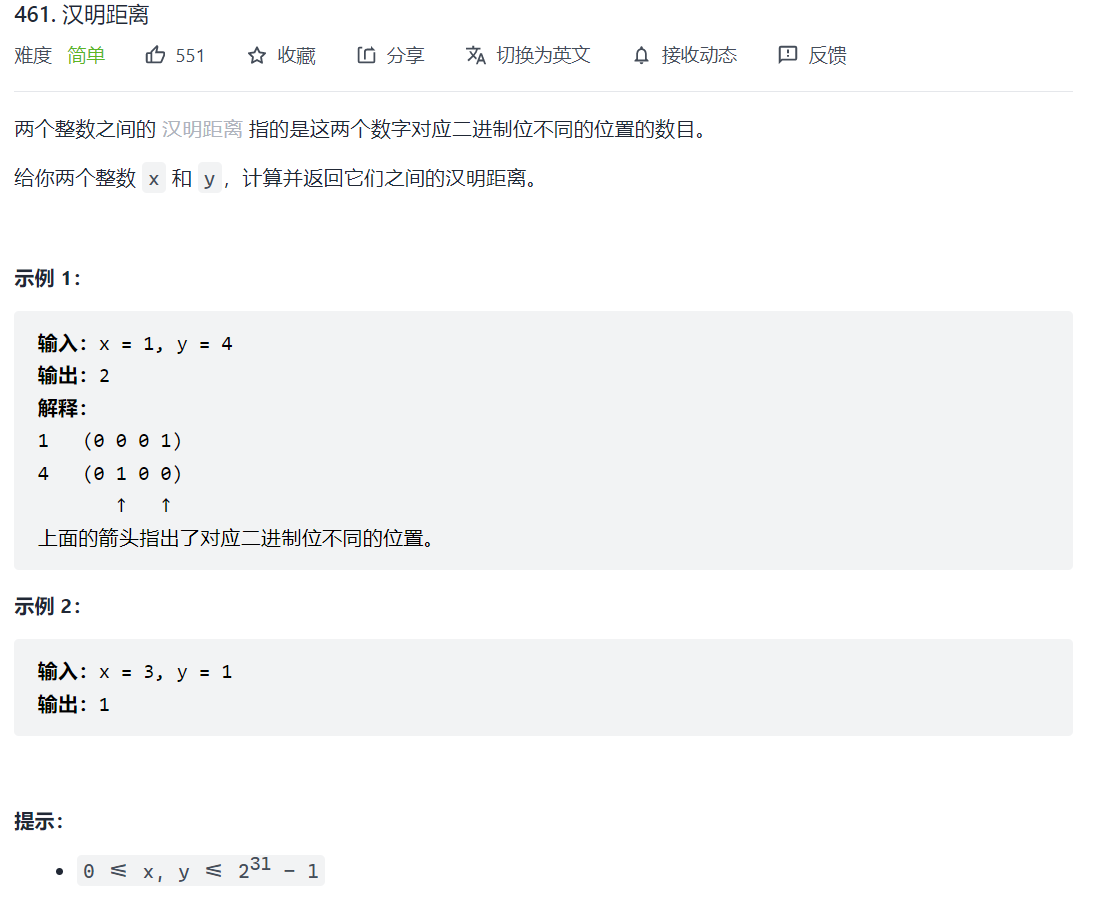
461. 汉明距离

image.png

思路一：移位实现计数

  1. class Solution {
  2. public:
  3.     int hammingDistance(int x, int y) {
  4.         // 先整体异或，然后取异或的结果的1之和
  5.         int z = x ^ y;
  6.         int res = 0;
  7.         while (z) {
  8.             res += z & 1;
  9.             z = z >> 1;
  10.         }
  11.         return res;
  12.     }
  13. };

麻烦一点

  1. class Solution {
  2. public:
  3.     int hammingDistance(int x, int y) {
  4.         // 逐位异或，相同为0，不同为1
  5.          unsigned helper = 1;
  6.          int res = 0;
  7.          for (int i = 0; i < 32; i++) {
  8.              int a = x & helper;
  9.              int b = y & helper;
  10.              res += a ^ b;
  11.              x = x >> 1;
  12.              y = y >> 1;
  13.          }
  14.          return res;
  15.     }
  16. };

思路二：调用API

  1. class Solution {
  2. public:
  3.     int hammingDistance(int x, int y) {
  4.          return __builtin_popcount(x ^ y);
  5.     }
  6. };

思路三：Brian Kernighan 算法

x & (x - 1)为x删除二进制中最左侧的1之后的结果，因此，我们可以逐个删除1，直到x为0，删除的次数就是1的个数

  1. class Solution {
  2. public:
  3.     int hammingDistance(int x, int y) {
  4.         int s = x ^ y, res = 0;
  5.         while (s) {
  6.             s &= s - 1;
  7.             res++;
  8.         }
  9.         return res;
  10.     }
  11. };

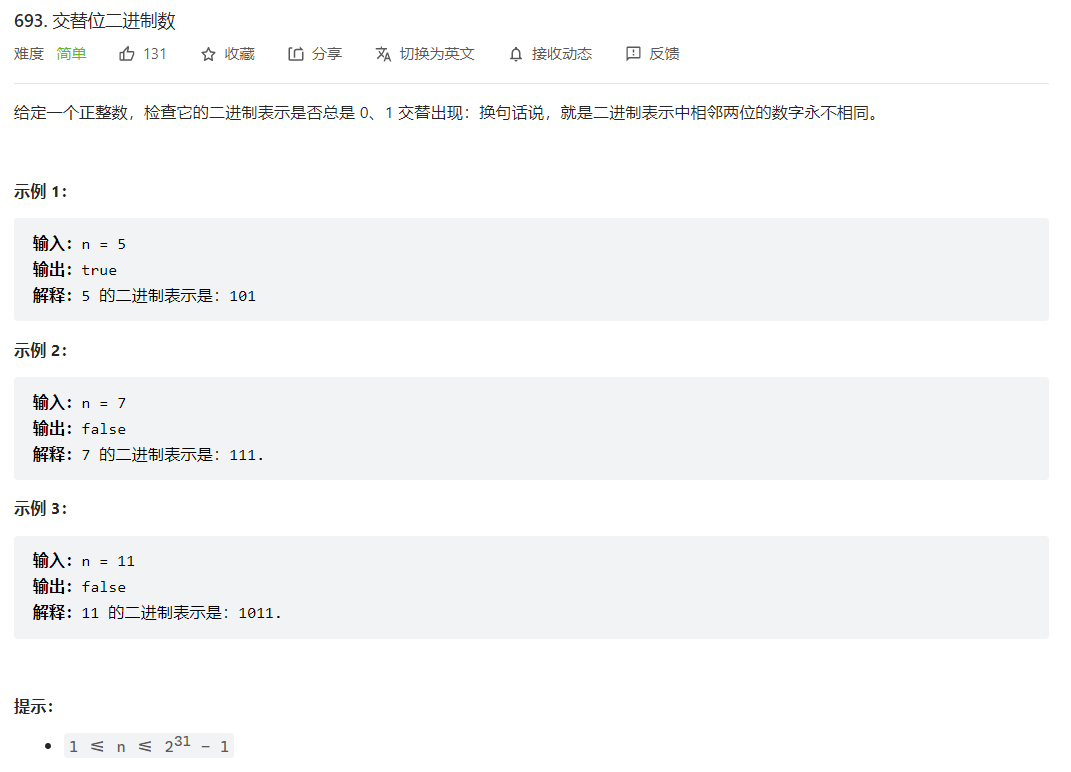
(20220328每日一题)693. 交替位二进制数

image.png

思路一：逐位比较

  1. class Solution {
  2. public:
  3.     bool hasAlternatingBits(int n) {
  4.         int lastBit = n & 1; // 1与运算得到数字的最后一位
  5.         n >>= 1; // n 右移一位
  6.         while (n) {
  7.             //通过异或（相同为0，不同为1）判断倒数第二位与最后一位是否相同
  8.             if ((n & 1) ^ lastBit) { // 如果两位不相同，异或结果为1，说明01交替出现
  9.                 lastBit = n & 1; // 更新最后一位
  10.                 n >>= 1; // n 继续右移
  11.             } else {
  12.                 return false; // 异或的结果是0，说明01不是交替出现的
  13.             }
  14.         }
  15.         return true;
  16.     }
  17. };

思路二

对输入 n 的二进制表示右移一位后，得到的数字再与 n 按位异或得到 a。当且仅当输入 n 为交替位二进制数时，a 的二进制表示全为 1（不包括前导 0）。这里进行简单证明：当 a 的某一位为 1 时，当且仅当 n 的对应位和其前一位相异。当 a 的每一位为 1 时，当且仅当 n 的所有相邻位相异，即n 为交替位二进制数。

将 a 与 a+1 按位与，当且仅当 a 的二进制表示全为 1 时，结果为 0。这里进行简单证明：当且仅当 a 的二进制表示全为 1 时，a+1 可以进位，并将原最高位置为 0，按位与的结果为 0。否则，不会产生进位，两个最高位都为 1，相与结果不为 0。

结合上述两步，可以判断输入是否为交替位二进制数。

class Solution {
public:
    bool hasAlternatingBits(int n) {
        long a = n ^ (n >> 1);
        return (a & (a + 1)) == 0;
    }
};