242. 有效的字母异位词">242. 有效的字母异位词
- 思路一
- 思路二
383. 赎金信">383. 赎金信
49. 字母异位词分组">49. 字母异位词分组
438. 找到字符串中所有字母异位词">438. 找到字符串中所有字母异位词
567. 字符串的排列">567. 字符串的排列
349. 两个数组的交集">349. 两个数组的交集
- 思路一
- 思路二
350. 两个数组的交集 II">350. 两个数组的交集 II
- 思路一
- 思路二
202. 快乐数">202. 快乐数
- 思路一
- 思路二
1. 两数之和">1. 两数之和
- 思路一：暴力法
- 思路二：哈希表
454. 四数相加 II">454. 四数相加 II
- 思路一
15. 三数之和">15. 三数之和
- 思路一：双指针
- *思路二：哈希法
18. 四数之和">18. 四数之和
146. LRU 缓存（双向链表）">146. LRU 缓存（双向链表）
460. LFU 缓存💦">460. LFU 缓存💦
- 哈希表+平衡二叉树
- 双哈希表+双向链表
128. 最长连续序列">128. 最长连续序列
76. 最小覆盖子串">76. 最小覆盖子串
- 滑动窗口+哈希表
  - 写法一，一一对比哈希表元素
  - 写法二，巧妙

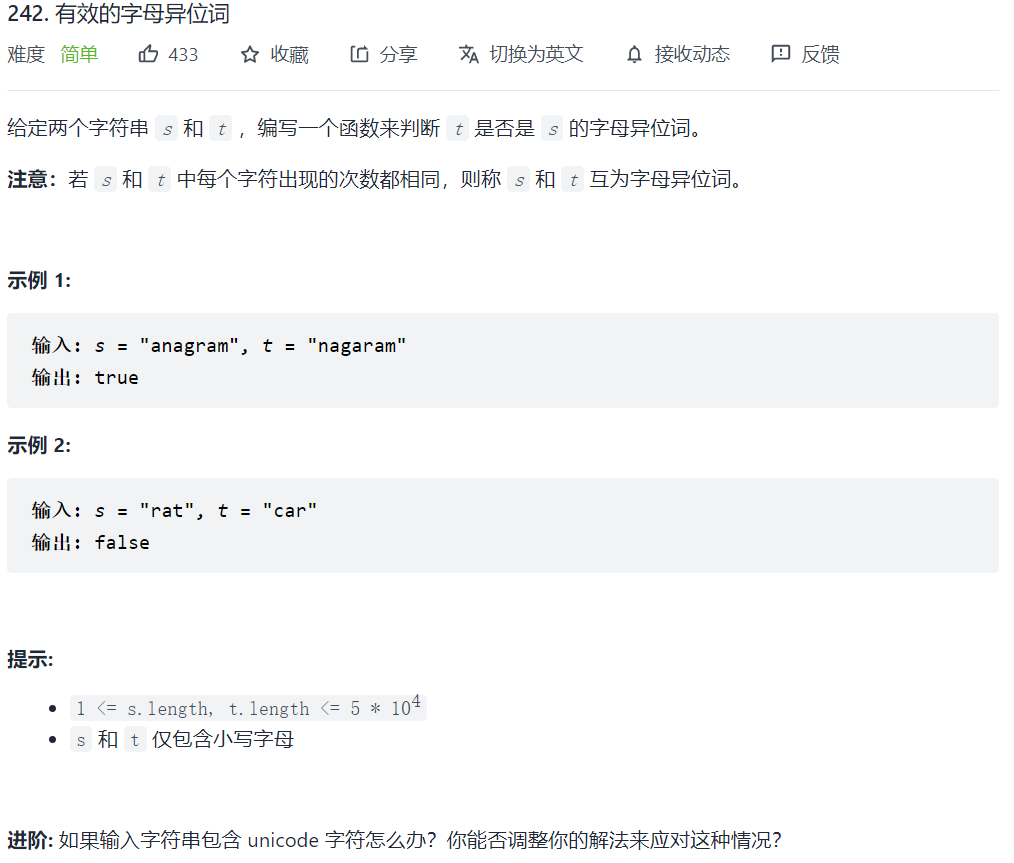
242. 有效的字母异位词

思路一

哈希表，将字符存入unordered_map，首先遍历s，可以得到每个字符出现的次数，然后遍历t，每碰到一个字符，都会将其次数减一，最后看unordered_map中的value值有没有非零元素，大于零表示该字母在s中出现的次数多，如果小于零表示该字母在t中出现的次数多，如果value都为0，那么是字母异位词

class Solution {
public:
    bool isAnagram(string s, string t) {
        if (s.size() != t.size()) return false;
        unordered_map<char, int> ht;
        for (auto ch: s) ht[ch]++;
        for (auto ch: t) ht[ch]--;
        for (auto p: ht) {
            if (p.second)
                return false;
        }
        return true;
    }
};

思路二

题目说了，s和t中只包含小写字母，那么可以用一个大小为26的数组(hash table)来存储字符出现的次数，最后判断的思路和用容器其实是一样的，只不过这个hash表是用的自定义的，但是思路一可以解决字符串中有其他字符的情况
比如判断一下字符串s= “aee”, t = “eae”。
哈希表 - 图2
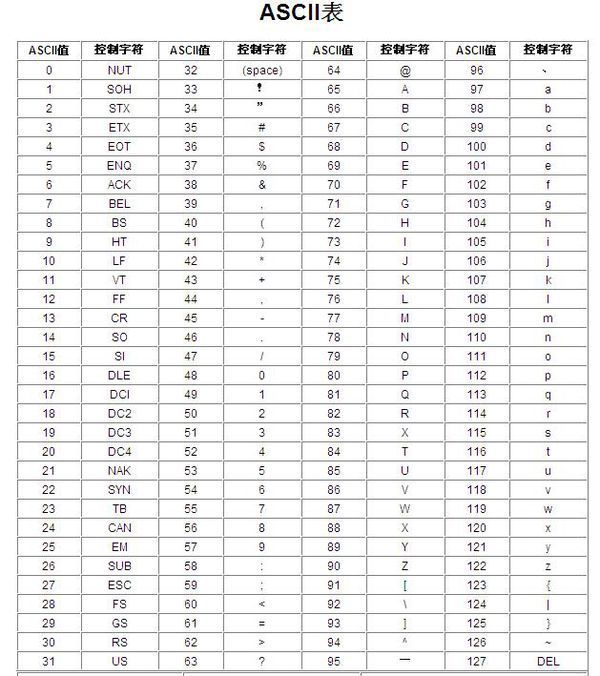
哈希表 - 图3
小写字母的ASCLL码的范围为 97 ~ 122，因此哈希函数设置为 x - 97 (x - 'a')

class Solution {
public:
    bool isAnagram(string s, string t) {
        if (s.size() != t.size()) return false;
        vector<int> ht(26, 0);
        for (auto ch: s) ht[ch - 'a']++;
        for (auto ch: t) ht[ch - 'a']--;
        for (int i = 0; i < 26; ++i)
            if (ht[i])
                return false;
        return true;
    }
};

也可以一趟遍历

class Solution {
public:
    bool isAnagram(string s, string t) {
        if (s.size() != t.size()) return false;
        vector<int> ht(26, 0);
        for (int i = 0; i < s.size(); ++i) {
           ht[s[i] - 'a']++;
           ht[t[i] - 'a']--;
        }

        for (int i = 0; i < 26; ++i)
            if (ht[i])
                return false;
        return true;
    }
};

思路三
将两个字符串排序，然后逐个字符比较

class Solution {
public:
    bool isAnagram(string s, string t) {
        if (s.length() != t.length()) {
            return false;
        }
        sort(s.begin(), s.end());
        sort(t.begin(), t.end());
        return s == t;
    }
};

383. 赎金信

思路一：暴力

// 时间复杂度: O(n^2)
// 空间复杂度：O(1)
class Solution {
public:
    bool canConstruct(string ransomNote, string magazine) {
        for (int i = 0; i < magazine.length(); i++) {
            for (int j = 0; j < ransomNote.length(); j++) {
                // 在ransomNote中找到和magazine相同的字符
                if (magazine[i] == ransomNote[j]) {
                    ransomNote.erase(ransomNote.begin() + j); // ransomNote删除这个字符
                    break;
                }
            }
        }
        // 如果ransomNote为空，则说明magazine的字符可以组成ransomNote
        if (ransomNote.length() == 0) {
            return true;
        }
        return false;
    }
};

这里时间复杂度是比较高的，而且里面还有一个字符串删除也就是erase的操作，也是费时的，当然这段代码也可以过这道题。

思路二：哈希

这道题和242题其实一样，只不过判断条件不同，如果前者某字符数量大于后者字符数量，即hash table对应的值小于0，则返回false。

class Solution {
public:
    bool canConstruct(string ransomNote, string magazine) {
        if (ransomNote.size() > magazine.size())
            return false;
        int ht[26] = {0};
        for (int i = 0; i < magazine.size(); ++i) {
            ht[magazine[i] - 'a']++;
            if (i < ransomNote.size())
                ht[ransomNote[i] - 'a']--;
        }
        for (int i = 0; i < 26; ++i)
            if (ht[i] < 0)
                return false;
        return true;

    }
};S

class Solution {
public:
    bool canConstruct(string ransomNote, string magazine) {
        // 仅包含小写字母，那么可以用26大小的数组来作为哈希表
        // 如果是Unicode编码，可以考虑使用unordered_map来做哈希表
        if (ransomNote.size() > magazine.size()) return false;
        int hash[26] = {0};
        for (auto ch: magazine) {
            hash[ch - 'a']++;
        }
        for (auto ch: ransomNote) {
            hash[ch - 'a']--;
            if (hash[ch - 'a'] < 0)
                return false;
        }
        return true; 
    }
};

49. 字母异位词分组

思路一

最直观的想法就是定义一个函数，用于判断字符串是否为异位词，然后遍历字符串数组，是的话就加到对应的数组中。
可以用unordered_map，key为排序后的字符串（因为异位词排序后必定是一致的），value为vector，用于保存异位词

class Solution {
public:
    vector<vector<string>> groupAnagrams(vector<string>& strs) {
        vector<vector<string>> res;
        unordered_map<string, vector<string>> ht;
        for (auto &str: strs) {
            string temp = str;
            sort(temp.begin(), temp.end());
            ht[temp].push_back(str);
        }
        for (auto p: ht)
            res.push_back(p.second);
        return res;
    }
};

思路二

计数排序 + 哈希表

由于互为字母异位词的两个字符串包含的字母相同，因此两个字符串中的相同字母出现的次数一定是相同的，故可以将每个字母出现的次数使用字符串表示，作为哈希表的键。

class Solution {
public:
    vector<vector<string>> groupAnagrams(vector<string>& strs) {
        unordered_map<string, vector<string>> um;
        for (auto &str: strs) {
            int helper[26] = {0};
            for (auto ch: str) {
                ++helper[ch - 'a'];
            }
            string temp;
            for (int i = 0; i < 26; ++i) {
                while (helper[i]--) {
                    temp.push_back('a' + i);
                }
            }
            um[temp].push_back(str);
        }
        vector<vector<string>> res;
        for (auto &p: um) {
            res.push_back(p.second);
        }
        return res;
    }
};

思路三（骚）

用质数（只能被一和自身整除，也就是不能拆）来表示每个字母，每个字符串用字母对应质数的乘积（由质数不能拆的性质知道，异位词的乘积必定是唯一的）表示，这样可以将字符串唯一映射到hash table中

这种思路面临的一个问题就是当字符串过长的时候，整数会溢出，不过思路还是可以借鉴一下的。

class Solution {
public:
    vector<vector<string>> groupAnagrams(vector<string>& strs) {
        vector<vector<string>> res;
        int prime[] = {2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101};
        unordered_map<long long, vector<string>> ht;
        for (auto &str: strs) {
            long long multy = 1;
            if (str.empty())
                multy = 0;
            else {
                for (auto ch: str) {
                    multy *= prime[ch - 'a'];
                }
            }
            ht[multy].push_back(str);
        }
        for (auto p: ht)
            res.push_back(p.second);
        return res;
    }
};

438. 找到字符串中所有字母异位词

思路一 ×

暴力解法（超时）

class Solution {
public:
    vector<int> findAnagrams(string s, string p) {
        if (s.size() < p.size())
            return {};
        vector<int> res;
        for(int i = 0; i < s.size() - p.size() + 1; ++i) {
            if (isAnagram(s.substr(i, p.size()), p))
                res.push_back(i);
        }
        return res;
    }

    bool isAnagram(string s, string t) {
        if (s.size() != t.size()) return false;
        vector<int> ht(26, 0);
        for (auto ch: s) ht[ch - 'a']++;
        for (auto ch: t) ht[ch - 'a']--;
        for (int i = 0; i < 26; ++i)
            if (ht[i])
                return false;
        return true;
    }
};

思路二滑动窗口

窗口大小为p.size()，将窗口内的字符存进哈希表中，如果满足是异位词子串，返回窗口起始位置下标，然后继续滑。

class Solution {
public:
    vector<int> findAnagrams(string s, string p) {
        if (s.size() < p.size())
            return {};
        vector<int> res;
        vector<int> ht1(26, 0);
        vector<int> ht2(26, 0);
        //init window
        for (int i = 0; i < p.size(); ++i) ht2[p[i] - 'a']++;
        for (int i = 0; i < p.size(); ++i) ht1[s[i] - 'a']++;
        // slide window
        for(int slow = 0, fast = p.size(); fast <= s.size(); ++fast, ++slow) {
            if (ht1 == ht2) res.push_back(slow);//如果窗口内的串是异位串，那么保存slow
            if (fast < s.size()) {//fast是开区间，滑动窗口时防止下标越界
                ht1[s[fast] - 'a']++;
                ht1[s[slow] - 'a']--;
            }              
        }
        return res;
    }
};

第二种写法：

class Solution {
public:
    vector<int> findAnagrams(string s, string p) {
        if (s.size() < p.size())
            return {};
        vector<int> res;
        vector<int> ht1(26, 0);
        vector<int> ht2(26, 0);
        //init window
        for (int i = 0; i < p.size(); ++i) ht2[p[i] - 'a']++;
        // slide window
        for(int slow = 0, fast = 0; fast < s.size(); ++fast) {
            ht1[s[fast] - 'a']++;
            if (fast >= p.size()) {
                ht1[s[slow] - 'a']--;
                slow++;
            }
            if (ht1 == ht2) res.push_back(slow);         
        }
        return res;
    }
};

思路三滑动窗口+双指针

不直接使用vector来比较两个哈希表是否相同
可以用快慢指针（分别指向窗口的左右端点）来处理窗口

先用哈希表记录p中字符的出现次数，然后遍历s，在哈希表中记录窗口中字符出现的次数，

用slow指向窗口的左端点，fast指向窗口的右端点，fast不断前移，表示向窗口中添加字符，假设窗口中某字符出现的次数为m，p中同样的字符出现的次数为n。每次添加后，都要判断一下 m是否大于n，
如果m > n，有下面两种情况：

窗口中出现了某字符，但是p中没有
窗口中某字符出现的次数大于p中字符出现的次数

都会使当前窗口不满足条件，那么将慢指针指向的字符次数减1，并让慢指针向前移动，直到任意的m都不大于n为止

然后考虑如何判断窗口中的子串和p互为异位字符串：
出现了m>n的情况，slow就会前移，也就是说窗口大小会收缩，当且仅当通过fast添加的元素，恰好是窗口中缺少的时，slow才不会前移，如果窗口大小 fast - slow + 1 == p.size()了，那么当前窗口和p是异位字符串，记录slow即可。

class Solution {
public:
    vector<int> findAnagrams(string s, string p) {
        int ht1[26] = {0}, ht2[26] = {0};
        for (auto ch : p) {
            ht2[ch - 'a']++;
        }
        vector<int> res;
        for (int slow = 0, fast = 0; fast < s.size(); fast++) {
            ht1[s[fast] - 'a']++;
            while (ht1[s[fast] - 'a'] > ht2[s[fast] - 'a']) {
                // 如果窗口里某个字符数量比p中多了，那么要移动窗口位置
                ht1[s[slow] - 'a']--;
                slow++;
            }
            if (fast - slow + 1 == p.size())
                res.push_back(slow);
        }
        return res;
    }
};

567. 字符串的排列

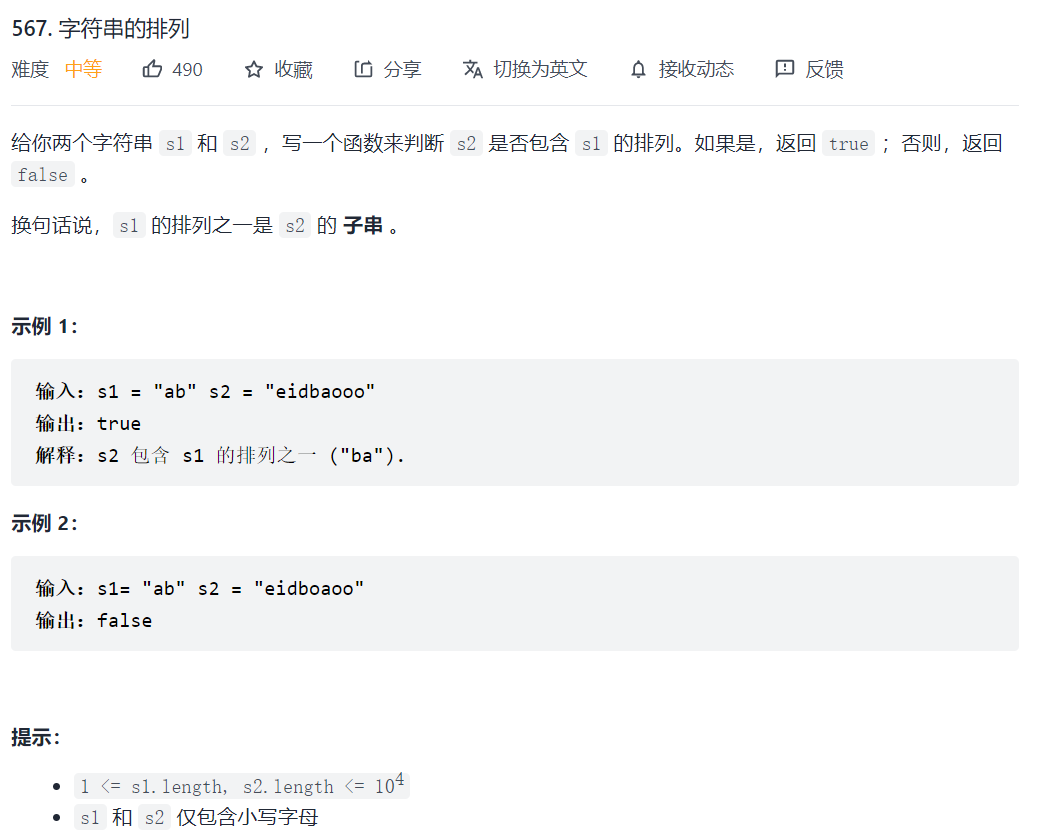
字符串的排列可以看作是异位字符串，如果找到了返回true，找不到则返回false

class Solution {
public:
    bool checkInclusion(string s1, string s2) {
        int ht1[26] = {0}, ht2[26] = {0};
        for (auto ch : s1) {
            ht2[ch - 'a']++;
        }
        for (int slow = 0, fast = 0; fast < s2.size(); fast++) {
            ht1[s2[fast] - 'a']++;
            while (ht1[s2[fast] - 'a'] > ht2[s2[fast] - 'a']) {
                ht1[s2[slow] - 'a']--;
                slow++;
            }
            if (fast - slow + 1 == s1.size()) {
                return true;
            }
        }
        return false;
    }
};

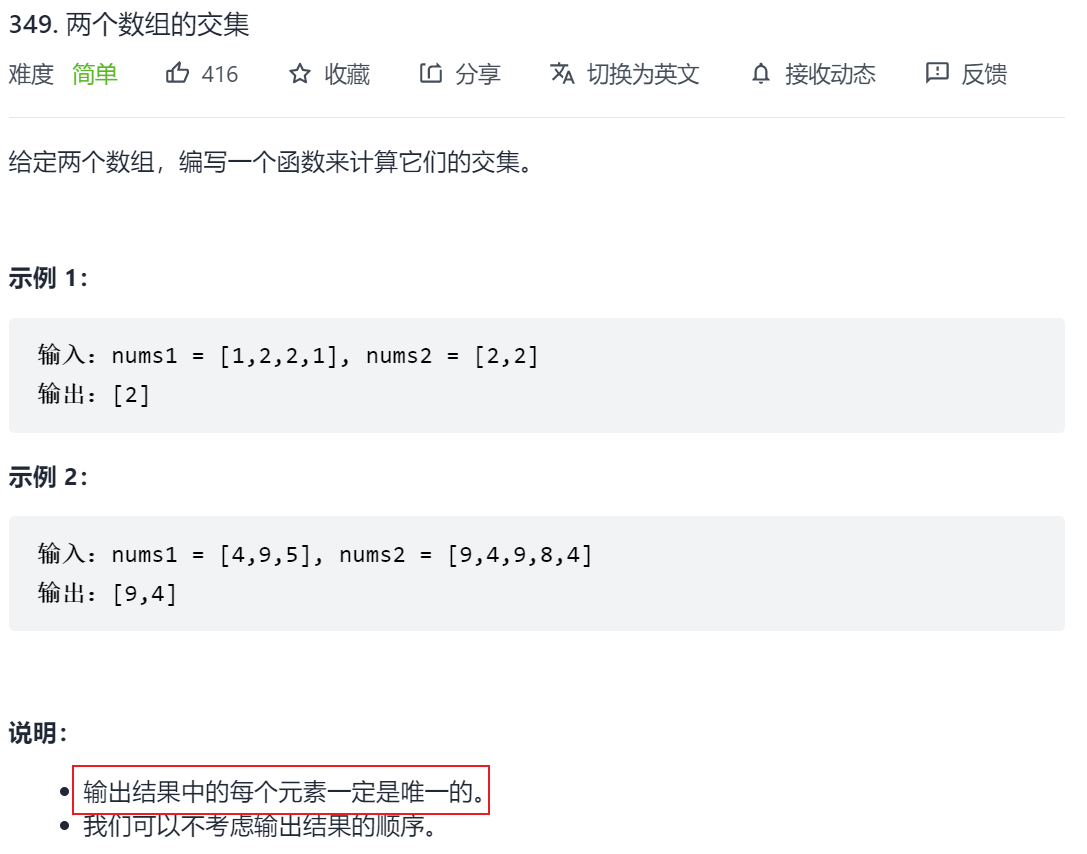
349. 两个数组的交集

思路一

可以用一个哈希表存储第一个数组中的元素，每当出现了一个元素，在哈希表中记录（因为最后结果中每个元素唯一，所以将value设为1，只用一次），扫描第二个数组，当数组中的元素出现在哈希表中时，将其添加到结果中，并将value置为0，表示已经输出

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        unordered_map<int, int> ht;
        vector<int> res;
        for (auto num : nums1) {
            ht[num] = 1;
        }
        for (auto num: nums2) {
            if (ht[num] == 1) {
                res.push_back(num);
                ht[num] = 0;
            }

        }
        return res;
    }
};

吐槽：一样的代码，一次8ms，一次0ms，太扯！

思路二

思路一种使用了容器unordered_map，它的底层是用的数组来实现的，而这道题并没有明确数的具体大小，因此，用数组作哈希表的话，可能会造成空间的浪费，并且每个元素之出现一次，并且不考虑输出的顺序，因此可以用集合这个容器：unordered_set

这种写法要在集合中擦除元素，以免结果中重复
find

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        unordered_set<int> ht(nums1.begin(), nums1.end());
        vector<int> res;
        for (auto num : nums2) {
            if (ht.find(num) != ht.end()) {//元素在集合中
                res.push_back(num);
                ht.erase(num);
            }  
        }
        return res;
    }
};

count

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        unordered_set<int> s(nums1.begin(), nums1.end());
        vector<int> res;
        for (auto num: nums2) {
            if (s.count(num)) {
                res.push_back(num);
                s.erase(num);
            }        
        }
        return res;
    }
};

这种写法，结果开始也存在unordered_set中，随后在转为vector

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        unordered_set<int> result_set; // 存放结果
        unordered_set<int> nums_set(nums1.begin(), nums1.end());
        for (int num : nums2) {
            // 发现nums2的元素 在nums_set里又出现过
            if (nums_set.find(num) != nums_set.end()) {
                result_set.insert(num);
            }
        }
        return vector<int>(result_set.begin(), result_set.end());
    }
};

350. 两个数组的交集 II

思路一

这道题和上一题的差别仅在于，结果中元素不是唯一的，也就是这个返回的结果是真正的交集，那么显然可以用map来记录每个元素的出现次数，同样，考虑到数值的大小不确定，使用map而不是unordered_map

class Solution {
public:
    vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
        map<int, int> ht;
        vector<int> res;
        for (auto num : nums1) {
            ht[num]++; //记录出现的次数
        }
        for (auto num : nums2) {
            if (ht[num] > 0) {
                res.push_back(num);
                ht[num]--;//每向结果中添加一次，记录的次数减一
            }
        }
        return res;
    }
};

为了降低空间复杂度，可以比较两个数组长度，用map来记录长度较小的数组，这也回答了进阶里的第二问

class Solution {
public:
    vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
        if (nums1.size() > nums2.size()) {
            return intersect(nums2, nums1);
        }
        map<int, int> ht;
        vector<int> res;
        for (auto num : nums1) {
            ht[num]++; //记录出现的次数
        }
        for (auto num : nums2) {
            if (ht[num] > 0) {
                res.push_back(num);
                ht[num]--;//每向结果中添加一次，记录的次数减一
            }
        }
        return res;
    }
};

思路二

进阶中有个问题，如果数组有序怎么办，如果数组有序的话，可以使用双指针
因此，就有了这种思路，首先将两个数组排序，然后用两个数组分别指向每个数组的头一个元素，

如果两元素不相等，那么较小者指针右移
如果相等，两指针同时右移

二指针有一个越界，则循环结束

class Solution {
public:
    vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
        vector<int> res;
        sort(nums1.begin(), nums1.end());
        sort(nums2.begin(), nums2.end());
        int i = 0;
        int j = 0;
        while (i < nums1.size() && j < nums2.size()) {
            if (nums1[i] == nums2[j]) {
                res.push_back(nums1[i]);
                i++;
                j++;
            } else if (nums1[i] > nums2[j]) {
                j++;
            } else {
                i++;
            }
        }
        return res;
    }
};

这个时间主要用在了排序上，没有用到额外空间。

如果数据量较大，存在磁盘上，无法一次将所有数据读到内存中，那么无法方便地对所有数据进行排序，因此选择第一种方法比较合适。

202. 快乐数

「快乐数」定义为：

对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1，也可能是无限循环但始终变不到 1。
如果可以变为 1，那么这个数就是快乐数。

思路一
直观上来说，判断一个数是否为快乐数，要先获得这个数每个位置上的数，然后计算其平方和，不断循环，直到平方和为1为止，如果能够变为1，就是快乐数，如果不能变为1，也就是需要无限循环。 既然无限循环，那么必然会有一个平方和会重复出现，如果出现了重复的平方和，那么终止循环，否则循环到平方和为1为止。
那么问题可以分解为以下几个步骤：
求该数的每一位的平方和
判断平方和是否为1
- 是1：返回true
- 不是1：
  - 判断平方和是否出现在哈希表中:
    - 出现：返回false
    - 未出现：将平方和放入哈希表 ```cpp class Solution { public: int getSquareSum(int n) { int sum = 0; while (n) { int tmp = n % 10; sum += tmp * tmp; n /= 10; } return sum; }
  bool isHappy(int n) { unordered_set ht; n = getSquareSum(n); while(n != 1) {
```
   if (ht.find(n) != ht.end()) {// n重复
      return false;
   } else { // n未重复
       ht.insert(n);
   }
   n = getSquareSum(n);
```
  } return true; } }; ```
  
  思路二
  快慢指针，类似于求环形链表的思想，想象将每次平方和存储在链表中，如果不是快乐数的话，这个链表必然有环：
slow每回求一次平方和，相当于每次扫描链表的一个节点
fast连续求两次平方和，相当于一次扫描两个节点

如果有环的话，必然fast和slow会相等，并且相等的值不为1，如果不存在环，那么fast会率先成为1，而slow也会最终成为1，只不过要慢一些.

比如，判断116是否为快乐数

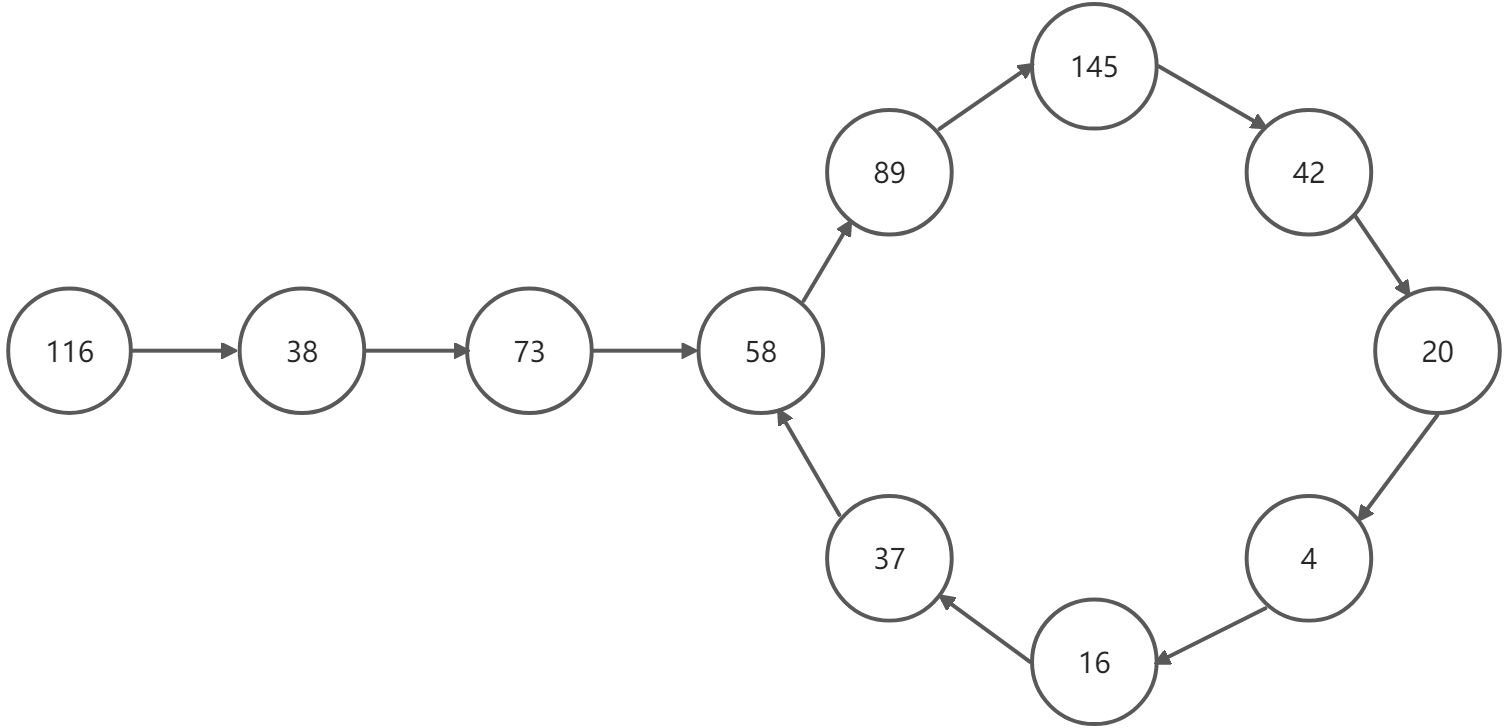
哈希表 - 图17
通过反复计算，相当于一个有环的链表，环的入口为58，那么fast和slow的值定会相等，并且不等于1

对于19来说：fast率先到达1后，会在1处原地循环，直到slow也等于1

哈希表 - 图18

这种解法不需要额外空间来存储每次的平方和，空间复杂度为O(1)
代码：

class Solution {
public:
    int getSquareSum(int n) {
        int sum = 0;
        while (n) {
            int tmp = n % 10;
            sum += tmp * tmp;
            n /= 10;
        }
        return sum;
    }

    bool isHappy(int n) {
        int fast = n, slow = n;
        do {
            slow = getSquareSum(slow);
            fast = getSquareSum(fast);
            fast = getSquareSum(fast);
        } while(slow != fast);

        if (fast == 1)
            return true;
        return false;
    }
};

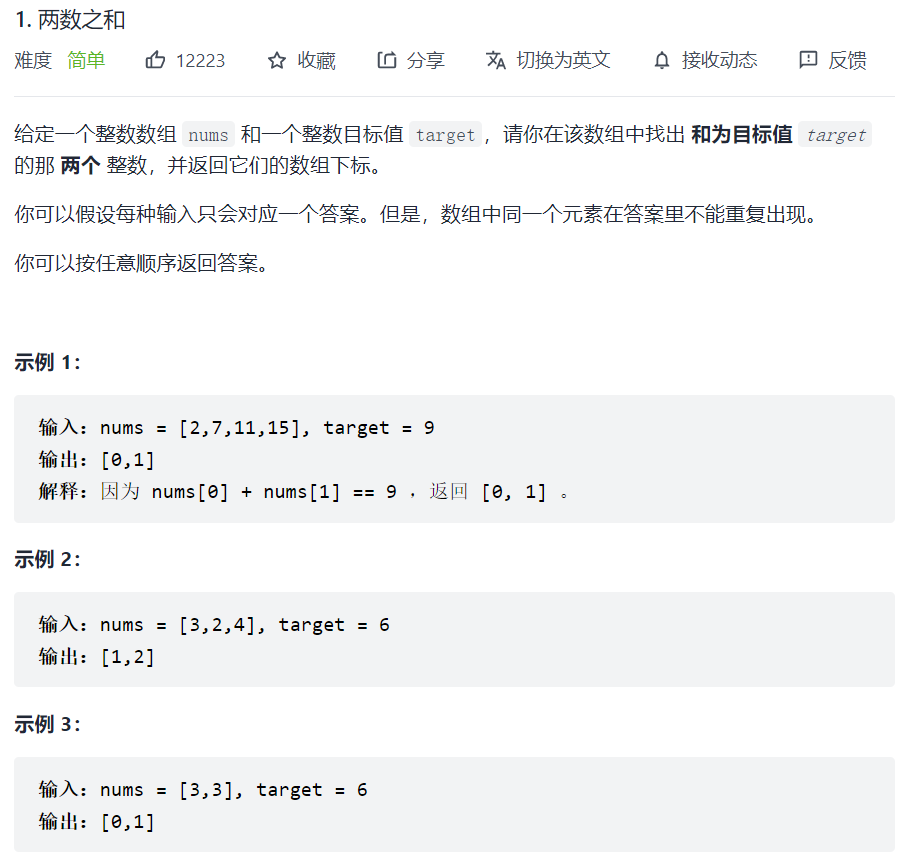
1. 两数之和

思路一：暴力法

两个循环遍历，不必多言

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        int i, j;
        for (i = 0; i < nums.size(); ++i) {
            for (j = i + 1; j < nums.size(); ++j)
                if (nums[i] + nums[j] == target)
                    return vector<int>{i, j};//题目说了一定有答案
        }
        return vector<int>{i, j};//语法要求有个return
    }
};

复杂度分析
时间复杂度：O(N^2)，其中 N 是数组中的元素数量。最坏情况下数组中任意两个数都要被匹配一次。
空间复杂度：O(1)。

思路二：哈希表

用哈希表来存储数组的的值，key为nums[i]，value是索引，遍历数组时，先判断哈希表中是否存在target - nums[i]，如果存在，那么返回 i 和 m[target - nums[i]]，吐过不存在，那么将数和索引保存到哈希表中

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int, int> um;
        for (int i = 0; i < nums.size(); ++i) {
            if (um.count(target - nums[i]))
                return {i, um[target - nums[i]]};
            um[nums[i]] = i;
        }
        return {};
    }
};

复杂度分析：

时间复杂度：O(n)，遍历一次数组即可
空间复杂度：O(n),哈希表

因为此题要返回原数组下标，所以排序后使用双指针不可取

454. 四数相加 II

这道题一看，我靠，直接暴力啊，遍历四个数组，每当碰见元素和为0的情况，直接count++

哈希表 - 图22
稍加思索后，发现遍历四个数组，那时间复杂度岂不是要哈希表 - 图23 ，所以代码连写都不写，定会超时。
那么要想其他办法了。
这道题和三数之和四数之和相比，简单很多，因为不用考虑重复问题

思路一

用一个unordered_map来记录前两个数组中两两元素之和，key为和，value为和出现的次数，然后遍历后两个数组，如果从这两个数组中挑出两个元素，它们的和与map中的和互为相反数，那么久满足条件，count += value，有点排列组合那味儿了。这样用了额外空间，空间复杂度为O(n)，时间复杂度降为O(n^2)

class Solution {
public:
    int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4) {
        unordered_map<int, int> count_sum; // key为前两个集合任意两元素之和，value为相加为key的两元素出现的次数
        for (auto a : nums1) {
            for (auto b : nums2) {
                count_sum[a + b]++;
            }
        }
        int count = 0;
        for (auto c : nums3) {
            for (auto d : nums4) {
                if (count_sum.find(0 - (c + d)) != count_sum.end()) {//满足和为0
                    count += count_sum[0 - (c + d)];
                }
            }
        }
        return count;
    }
};

class Solution {
public:
    int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4) {
        unordered_map<int, int> um;
        for (auto &a: nums1) {
            for (auto &b: nums2) {
                ++um[a + b]; // 数对和出现的次数+1
            }
        }
        int res = 0;
        for (auto &c: nums3) {
            for (auto &d: nums4) {
                if (um.count(-(c + d))) {
                    res += um[-(c + d)]; // 如果有数对和与他们的和是相反数，那么数对有多少个，就能凑出多少个tuple
                }
            }
        }
        return res;
    }
};

15. 三数之和

思路一：双指针

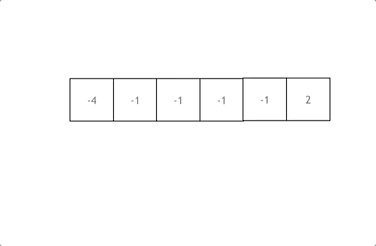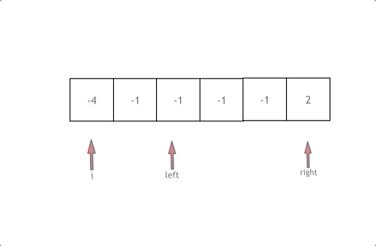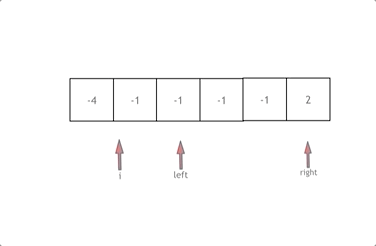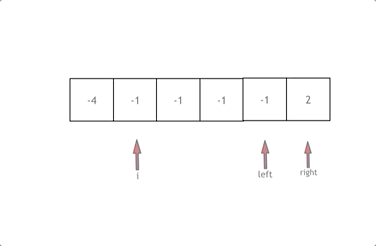
哈希表 - 图26
拿这个nums数组来举例，首先将数组排序，然后有一层for循环，i从下标0的地方开始，同时定一个下标left 定义在i+1的位置上，定义下标right 在数组结尾的位置上。
依然还是在数组中找到 abc 使得a + b + c = 0，我们这里相当于 a = nums[i] b = nums[left] c = nums[right]。
接下来如何移动left 和right呢，如果nums[i] + nums[left] + nums[right] > 0 就说明此时三数之和大了，因为数组是排序后了，所以right下标就应该向左移动，这样才能让三数之和小一些。
如果 nums[i] + nums[left] + nums[right] < 0 说明此时三数之和小了，left 就向右移动，才能让三数之和大一些，直到left与right相遇为止。
换一种思路理解，就是固定i，在 i + 1到 nums.size() - 1之间寻找两个数，使它们的和为-i，

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        vector<vector<int>> res;
        sort(nums.begin(), nums.end());
        for (int i = 0; i < nums.size(); i++) {
            if (nums[i] > 0) {//如果排序后第一个元素比0大，那么无论如何不可能相加为0
                return res;
            }

            if (i > 0 && nums[i] == nums[i - 1]) continue; // 如果i指向的元素和前一个一样，那么得到的元组会重复

            int left = i + 1;
            int right = nums.size() - 1;
            while (left < right) {
                if (nums[i] + nums[left] + nums[right] > 0) {
                    right--;
                } else if (nums[i] + nums[left] + nums[right] < 0) {
                    left++;
                } else {
                    res.push_back({nums[i], nums[left], nums[right]});
                    //去重
                    while (left < right && nums[right] == nums[right - 1]) right--;
                    while (left < right && nums[left] == nums[left + 1]) left++;

                    //如果不重复，两指针同时收缩
                    right--;
                    left++;
                }
            }
        }
        return res;
    }
};

*思路二：哈希法

两层for循环就可以确定 a 和b 的数值了，可以使用哈希法来确定 0-(a+b)是否在数组里出现过，其实这个思路是正确的，但是我们有一个非常棘手的问题，就是题目中说的不可以包含重复的三元组。
把符合条件的三元组放进vector中，然后再去重，这样是非常费时的，很容易超时，也是这道题目通过率如此之低的根源所在。
去重的过程不好处理，有很多小细节，如果在面试中很难想到位。
时间复杂度可以做到O(n^2)，但还是比较费时的，因为不好做剪枝操作。

因为在去重的操作中有很多细节需要注意，在面试中很难直接写出没有bug的代码，所以这道题记住双指针法就好，哈希法回头复习。

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        vector<vector<int>> result;
        sort(nums.begin(), nums.end());
        // 找出a + b + c = 0
        // a = nums[i], b = nums[j], c = -(a + b)
        for (int i = 0; i < nums.size(); i++) {
            // 排序之后如果第一个元素已经大于零，那么不可能凑成三元组
            if (nums[i] > 0) {
                continue;
            }
            if (i > 0 && nums[i] == nums[i - 1]) { //三元组元素a去重
                continue;
            }
            unordered_set<int> set;
            for (int j = i + 1; j < nums.size(); j++) {
                if (j > i + 2
                        && nums[j] == nums[j-1]
                        && nums[j-1] == nums[j-2]) { // 三元组元素b去重
                    continue;
                }
                int c = 0 - (nums[i] + nums[j]);
                if (set.find(c) != set.end()) {
                    result.push_back({nums[i], nums[j], c});
                    set.erase(c);// 三元组元素c去重
                } else {
                    set.insert(nums[j]);
                }
            }
        }
        return result;
    }
};

18. 四数之和

四数之和，和15.三数之和(opens new window)是一个思路，都是使用双指针法, 基本解法就是在15.三数之和(opens new window)的基础上再套一层for循环。
但是有一些细节需要注意，例如：不要判断nums[k] > target 就返回了，三数之和可以通过 nums[i] > 0 就返回了，因为 0 已经是确定的数了，四数之和这道题目 target是任意值。（大家亲自写代码就能感受出来）
15.三数之和(opens new window)的双指针解法是一层for循环num[i]为确定值，然后循环内有left和right下表作为双指针，找到nums[i] + nums[left] + nums[right] == 0。
四数之和的双指针解法是两层for循环nums[k] + nums[i]为确定值，依然是循环内有left和right下表作为双指针，找出nums[k] + nums[i] + nums[left] + nums[right] == target的情况，三数之和的时间复杂度是O(n^2)，四数之和的时间复杂度是O(n^3) 。
那么一样的道理，五数之和、六数之和等等都采用这种解法。
对于15.三数之和(opens new window)双指针法就是将原本暴力O(n^3)的解法，降为O(n^2)的解法，四数之和的双指针解法就是将原本暴力O(n^4)的解法，降为O(n^3)的解法。
之前我们讲过哈希表的经典题目：454.四数相加II(opens new window)，相对于本题简单很多，因为本题是要求在一个集合中找出四个数相加等于target，同时四元组不能重复。
而454.四数相加II(opens new window)是四个独立的数组，只要找到A[i] + B[j] + C[k] + D[l] = 0就可以，不用考虑有重复的四个元素相加等于0的情况，所以相对于本题还是简单了不少！
我们来回顾一下，几道题目使用了双指针法。
双指针法将时间复杂度O(n^2)的解法优化为 O(n)的解法。也就是降一个数量级，题目如下：

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        sort(nums.begin(), nums.end());
        vector<vector<int>> res;
        for (int k = 0; k < nums.size(); k++) {
            //去重
            if (k > 0 && nums[k] == nums[k - 1])
                continue;

            for (int i = k + 1; i < nums.size(); i++) {
                //去重
                if (i > k + 1 && nums[i] == nums[i - 1])
                    continue;
                int left = i + 1, right = nums.size() - 1;
                while (left < right) {
                    if (nums[k] + nums[i] + nums[left] + nums[right] > target) right--;
                    else if (nums[k] + nums[i] + nums[left] + nums[right] < target) left++;
                    else {
                        res.push_back({nums[k], nums[i], nums[left], nums[right]});
                        //去重
                        while (left < right && nums[right] == nums[right - 1]) right--;
                        while (left < right && nums[left] == nums[left + 1]) left++;
                        //收缩
                        right--;
                        left++;
                    }
                }
            }
        }
        return res;
    }
};

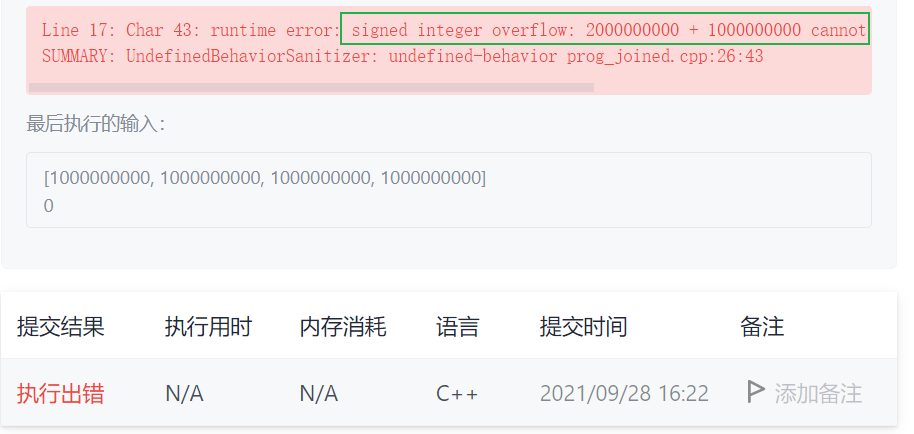
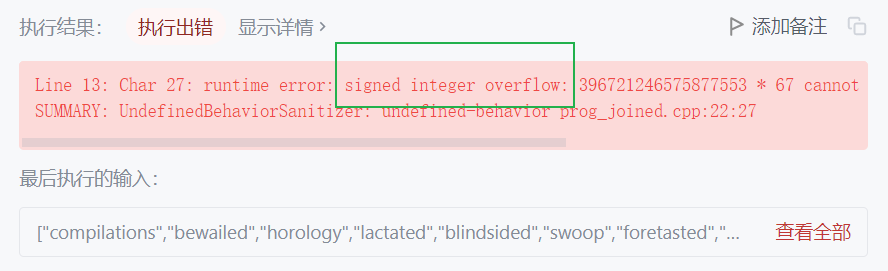
这个测试用例绝了，tmd。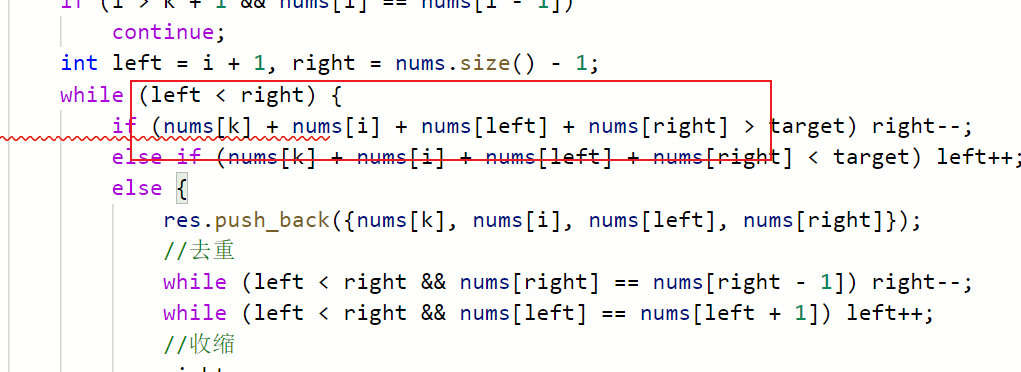

整数太大了，发生溢出，考虑作差。

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        sort(nums.begin(), nums.end());
        vector<vector<int>> res;
        for (int k = 0; k < nums.size(); k++) {
            //去重
            if (k > 0 && nums[k] == nums[k - 1])
                continue;

            for (int i = k + 1; i < nums.size(); i++) {
                //去重
                if (i > k + 1 && nums[i] == nums[i - 1])
                    continue;

                int left = i + 1, right = nums.size() - 1;
                while (left < right) {
                    // nums[k] + nums[i] + nums[left] + nums[right] > target 会溢出
                    if (nums[i] + nums[k] > target - nums[left] - nums[right]) right--;
                    else if (nums[i] + nums[k] < target - nums[left] - nums[right]) left++;
                    else {
                        res.push_back({nums[k], nums[i], nums[left], nums[right]});
                        //去重
                        while (left < right && nums[right] == nums[right - 1]) right--;
                        while (left < right && nums[left] == nums[left + 1]) left++;
                        //收缩
                        right--;
                        left++;
                    }
                }
            }
        }
        return res;
    }
};

最后终于通过
复杂度分析：
时间复杂度：双指针，将暴力O(n^4)降为O(n^3)
空间复杂度：没有使用额外空间 O(1)

146. LRU 缓存（双向链表）

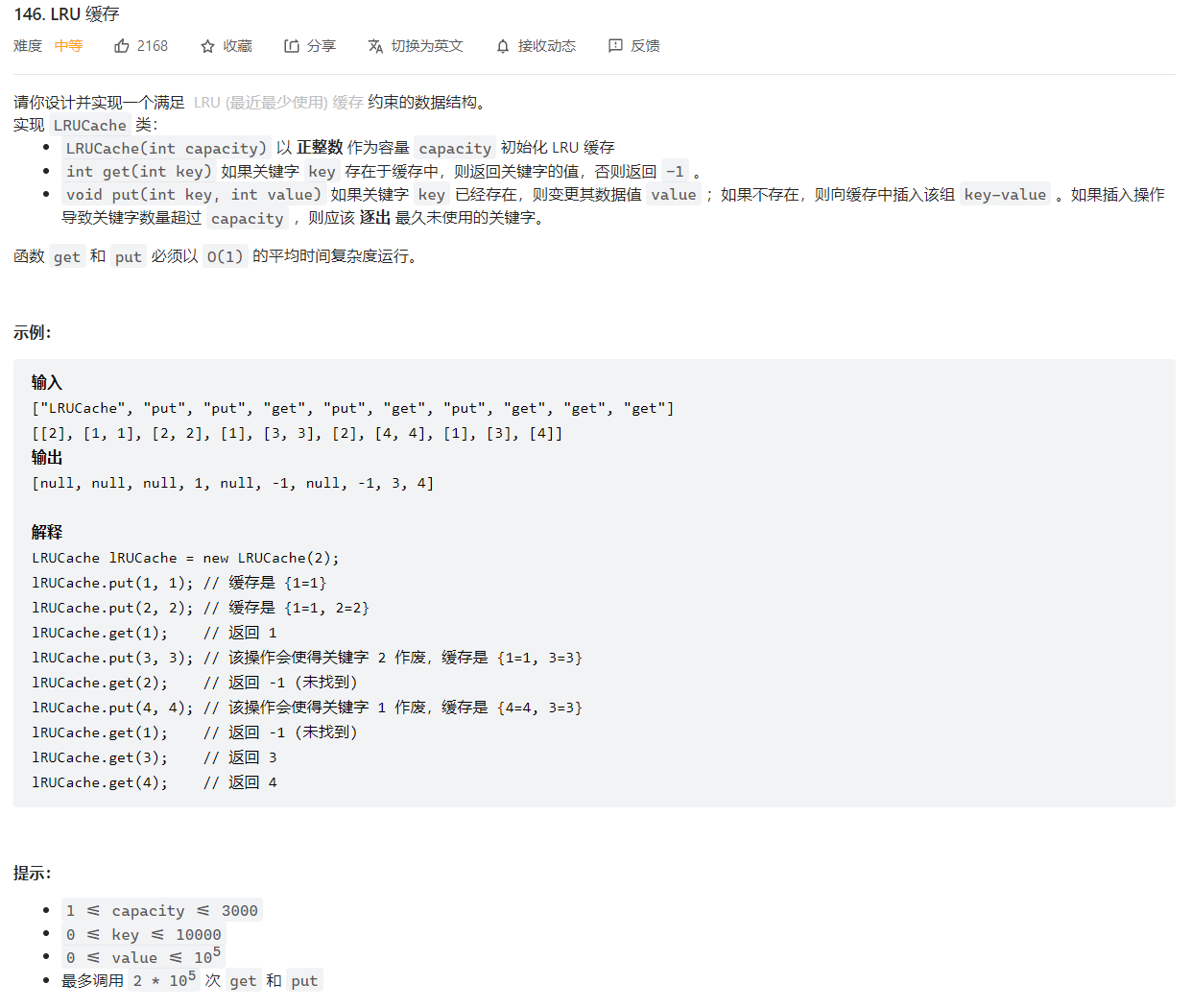
这道题考察数据结构：双向链表+哈希表

缓存采用双向链表作为数据结构，每当访问一个节点（get、put）时，将其移动至表头，这样表尾就是最久未使用的节点，当需要替换时，替换表尾。

哈希表用于定位，在O(1)时间复杂度找到要找的节点

get
- 如果key不存在，返回-1
- 如果key存在，将节点移动至表头，返回节点值
put
- 新建节点插入表头
  - 插入后容量未满
  - 插入后容量超出：删除尾结点
- key已经存在
  - 更新其值，将其移动至表头

涉及链表的插入删除操作时，一般设置虚拟头结点（如果是双向的加上虚拟尾结点）可以避免讨论（比如删除第一个元素）

class LRUCache {
public:
    struct MyList {
        int key; // 删除节点时用
        int value;
        MyList* next;
        MyList* pre;
        MyList() : key(0), value(0), next(nullptr), pre(nullptr) {}
        MyList(int x, int y) : key(x), value(y), next(nullptr), pre(nullptr) {}
    };
    // 构造函数
    LRUCache(int capacity) : capacity(capacity), size(0) { // 初始化
        head = new MyList();
        tail = new MyList();
        head->next = tail;
        tail->pre = head;
    }
    // get
    int get(int key) {
        if (!um.count(key)) {
            return -1;
        }
        MyList* node = um[key];
        moveToHead(node); // 移动到头部
        return node->value;
    }

    void put(int key, int value) {
        if (!um.count(key)) {
            MyList* node = new MyList(key, value);
            um[key] = node;
            addToHead(node); // 添加到头部
            ++size;
            if (size > capacity) {
                removeTail(); // 删除尾部节点
            }
        } else {
            MyList* node = um[key];
            node->value = value;
            moveToHead(node); // 移动到头部
        }
    }

    // 添加节点至头部
    void addToHead(MyList* node) {
        node->next = head->next;
        head->next = node;
        node->pre = node->next->pre;
        node->next->pre = node;
    }

    void moveToHead(MyList* node) {
        // 从当前位置移除
        removeNode(node);
        // 插入头部
        addToHead(node);
    }

    void removeNode(MyList* node) {
        node->pre->next = node->next;
        node->next->pre = node->pre;
    }

    void removeTail() {
        MyList* tmp = tail->pre;
        um.erase(tmp->key);
        removeNode(tmp);
        --size;
        delete tmp;
    }

    unordered_map<int, MyList*> um;
    MyList* head;
    MyList* tail;
    int size;
    int capacity;
};

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache* obj = new LRUCache(capacity);
 * int param_1 = obj->get(key);
 * obj->put(key,value);
 */

时间复杂度：对于 put 和 get 都是 O(1)。
空间复杂度：O(capacity)，因为哈希表和双向链表最多存储 capacity个元素

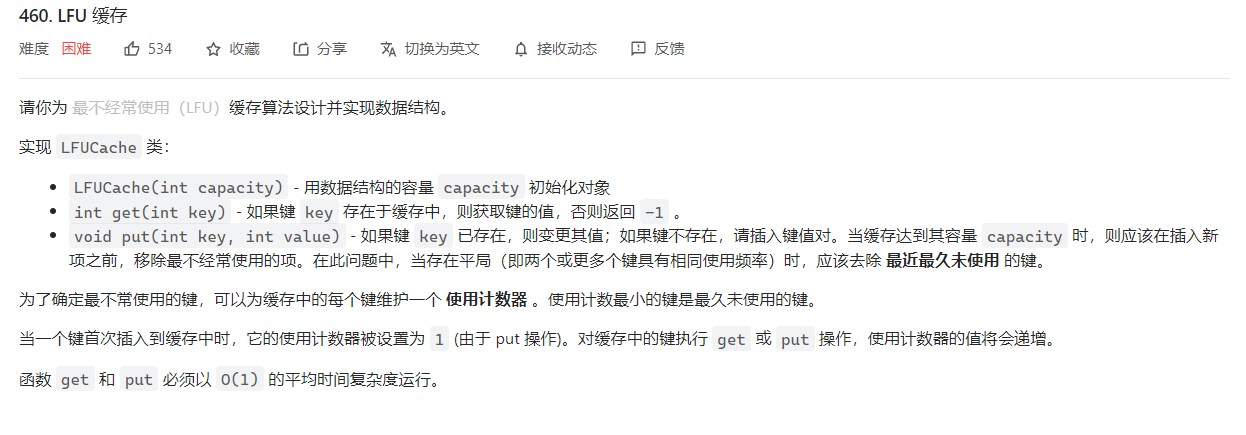
460. LFU 缓存💦

哈希表+平衡二叉树

定义缓存类，类中数据成员包括使用的频率和时间戳(最后一次使用的时间)，同时重载小于号（优先按照使用频率排序，使用频率相同时按照时间戳排序）用于排序。维护一个平衡二叉树，C++中是set。set的最左边的元素就是最不常使用的那一个。同时使用哈希表来实现快速查找key对应的缓存。

get：
- key不存在返回-1
- key存在，将set中的元素删除，更新其使用频率和时间戳后放回，返回value
put：
- 如果不存在则插入，如果容量已满，删除set.begin()指向的元素（最不常使用的），新建缓存，将其插入哈希表和集合中
- 如果存在的话，更新value、使用频率、时间戳。更新的时候和get类似，维护set的有序性，先将原来的删除再插入更新后的。

class LFUCache {
public:
    // 缓存类
    struct Node {
        int time; // 最近一次使用的时间
        int fre; // 使用的频率
        int key;
        int value;
        Node() = default;
        Node(int time, int fre, int k, int v) : time(time), fre(fre), key(k), value(v) {}
        // 重载小于号，用于排序
        bool operator <(const Node& rhs) const {
            return fre == rhs.fre ? time < rhs.time : fre < rhs.fre;
        }
    };
    // constructor
    LFUCache(int capacity) : time(0), capacity(capacity){
        cache.clear();
        se.clear();
    }
    // get
    int get(int key) {
        if (capacity == 0) return -1;
        if (!cache.count(key)) return -1;

        Node node = cache[key];
        se.erase(node); // 删除旧缓存

        node.fre += 1; // 使用频率增加
        node.time = ++time; // 更新最近一次使用的时间
        se.insert(node); // 插入更新后的缓存
        cache[key] = node;
        return node.value;
    }

    // put
    void put(int key, int value) {
        if (capacity == 0) return;
        if (!cache.count(key)) {
            if (cache.size() == capacity) { // 容量不够的话先删除最不常使用的缓存
                cache.erase(se.begin()->key);
                se.erase(se.begin());     
            }
            Node node(++time, 1, key, value);
            cache[key] = node;
            se.insert(node);
        } else {
            Node node = cache[key];
            se.erase(node);
            node.fre++;
            node.time = ++time;
            node.value = value;
            se.insert(node);
            cache[key] = node;
        }
    }

    int time; // 系统时间
    int capacity; // 容量
    unordered_map<int, Node> cache; // key: key value: Node
    set<Node> se; // 按照顺序存放每个缓存
};

/**
 * Your LFUCache object will be instantiated and called as such:
 * LFUCache* obj = new LFUCache(capacity);
 * int param_1 = obj->get(key);
 * obj->put(key,value);
 */

时间复杂度 O(logN)，get和put的时间都用在了平衡二叉树的查找上
空间复杂度O(capacity)

这个思路复杂度没有达到O(1)，还需改进

双哈希表+双向链表

可以维护两个哈希表：

freq_table: key是缓存的频率，值为一个双向链表
key_table: key是缓存的键，值是双向链表的迭代器

定义缓存类，存储键值频率。
每当get一个缓存时，先在key_table中获取其迭代器，然后通过迭代器访问该缓存；访问后可以将旧的缓存删除，更新使用频率后形成新的缓存，将其插入更高频率链表表头。通过哈希表和链表进行插入删除，时间复杂度都是O(1)。
这样，当get和put时，都是在查找一个缓存，只不过put需要更新value值
当put的key不存在时，要新插入一个缓存，如果缓存已满，就可以删除频率最小链表的尾结点。因为最近使用的都是插在头部，所以尾部的一定是同一频率最久未使用过的。最小频率可以用一个变量来存储。
细节看代码。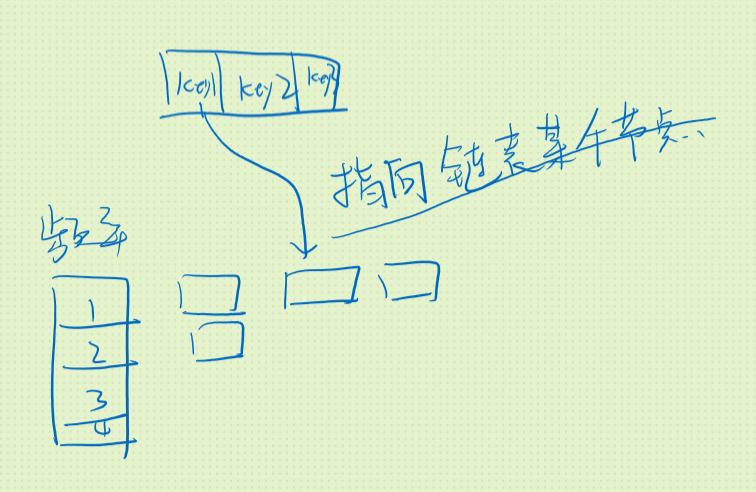

class LFUCache {
public:
    struct Node {
        int freq, key, value;
        Node() = default;
        Node(int freq, int key, int value) : freq(freq), key(key), value(value) {}
    };
    LFUCache(int capacity) : minfreq(1), capacity(capacity){
        key_table.clear();
        freq_table.clear();
    }

    int get(int key) {
        if (capacity == 0) return -1;
        if (!key_table.count(key)) {
            return -1;
        }
        auto it = key_table[key]; // 取迭代器
        int freq = it->freq, value = it->value; // 将值取出
        freq_table[freq].erase(it); // 将旧的缓存删除
        if (freq_table[freq].empty()) { // 如果删除之后该频率下没有东西，删除该链表
            freq_table.erase(freq);
            if (minfreq == freq) minfreq++; // 更新最小频率
        }
        freq++; // 频率加一
        Node node(freq, key, value);
        freq_table[freq].push_front(node); // 插入到freq + 1的表头
        key_table[key] = freq_table[freq].begin(); // 更新迭代器
        return value;
    }

    void put(int key, int value) {
        if (capacity == 0) return;
        if (!key_table.count(key)) { // 没有则插入
            if (key_table.size() == capacity) { // 如果容量满了，先删除最不常用的
                while (freq_table[minfreq].empty()) minfreq++;
                key_table.erase(freq_table[minfreq].back().key);
                freq_table[minfreq].pop_back();
                if (freq_table[minfreq].empty()) {
                    freq_table.erase(minfreq);
                }
            }
            minfreq = 1; // 有新插入的节点，最小频率设为1
            Node node(1, key, value);
            freq_table[1].push_front(node);
            key_table[key] = freq_table[1].begin();
        } else { // 与get操作类似
            auto it = key_table[key];
            int freq = it->freq;
            freq_table[freq].erase(it);
            if (freq_table[freq].empty()) {
                freq_table.erase(freq);
                if (freq == minfreq) minfreq++;
            }
            freq++;
            Node node(freq, key, value);
            freq_table[freq].push_front(node);
            key_table[key] = freq_table[freq].begin();
        }
    }
    int minfreq; // 最小频率，删除某节点时用
    int capacity; // 容量
    unordered_map<int, list<Node>::iterator> key_table; // key: key  value: iterator
    unordered_map<int, list<Node>> freq_table; // key: 频率  value: 双向链表

};

/**
 * Your LFUCache object will be instantiated and called as such:
 * LFUCache* obj = new LFUCache(capacity);
 * int param_1 = obj->get(key);
 * obj->put(key,value);
 */

时间复杂度O(1)
空间复杂度O(logN)

128. 最长连续序列

用哈希表集合记录数组中的元素，每当访问一个元素x时，尝试寻找是否存在x+1使之构成连续序列。优化：如果x-1存在于集合中，可以直接跳过，因为从x搜索到的连续序列的长度一定不会超过从x-1开始搜索

class Solution {
public:
    int longestConsecutive(vector<int>& nums) {
        unordered_set<int> s;
        for (auto& num : nums) s.insert(num);

        int res = 0, cnt;
        for (auto& num : nums) {
            if (!s.count(num - 1)) {
                cnt = 1;
                int x = num;
                while (s.count(x + 1)) {
                    cnt++;
                    x++;
                }
            }
            res = max(res, cnt);
        }
        return res;
    }
};

76. 最小覆盖子串

滑动窗口+哈希表

写法一，一一对比哈希表元素

class Solution {
public:
    typedef unordered_map<char, int> UCI;
    // 判断是否包含所有字符
    bool check(UCI& hs, UCI&ht) {
        for (auto &[ch, cnt] : ht) {
            if (hs[ch] < cnt) return false;
        }
        return true;
    }
    string minWindow(string s, string t) {
        UCI hs, ht;
        for (auto& ch : t) ht[ch]++;
        int n = t.size(), cnt = 0;
        int len = 1e5 + 10, start = 0;

        for (int i = 0, j = 0; i < s.size(); i++) {
            char ch = s[i];
            hs[ch]++;
            while (hs[s[j]] > ht[s[j]]) hs[s[j++]]--; // 有多余的可以删掉
            if (len > i - j + 1 && check(hs, ht)) {
                    len = i - j + 1;
                    start = j;
            }
        }
        return len == 1e5 +10 ? "" : s.substr(start, len);
    }
};

写法二，巧妙

维护一个哈希表来记录子串中涵盖的字符数，维护一个变量记录子串中有效的字符数（新增加的字符刚好可以用来覆盖t中的一个字符）个数，如果有效字符等于t的长度，那么考虑更新一下子串

class Solution {
public:
    string minWindow(string s, string t) {
        unordered_map<char, int> hs, ht;
        for (auto& ch : t) ht[ch]++;
        int n = t.size(), cnt = 0;
        string res;
        for (int i = 0, j = 0; i < s.size(); i++) {
            char ch = s[i];
            hs[ch]++;
            if (hs[ch] <= ht[ch]) cnt++; // 新加入的字符有用
            while (hs[s[j]] > ht[s[j]]) hs[s[j++]]--; // 有多余的可以删掉
            if (cnt == n) {
                if (res.empty() || i - j + 1 < res.size()) {
                    res = s.substr(j, i - j + 1);
                }
            }
        }
        return res;
    }
};

哈希表

思路一

思路二