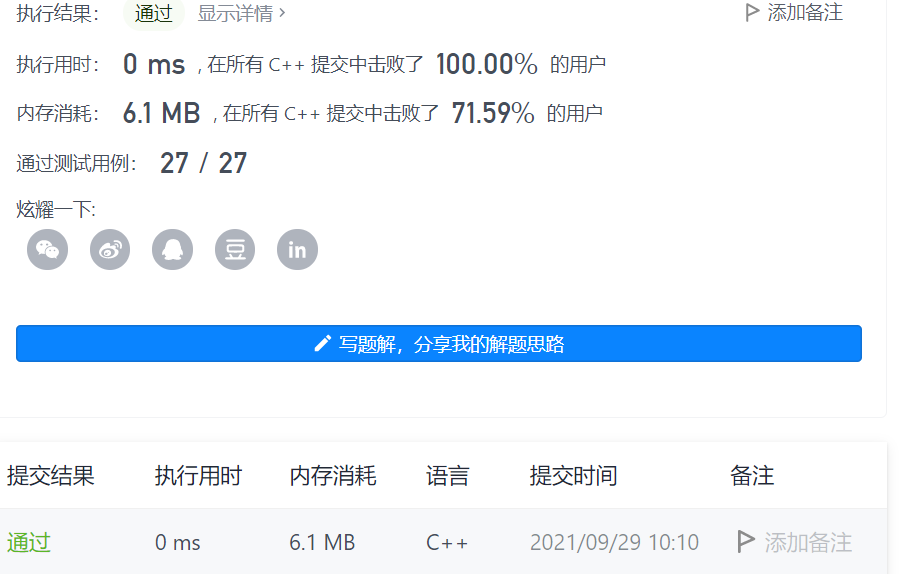
剑指 Offer 05. 替换空格

思路一：使用额外空间

新建一个字符串res，扫描原字符串，若是空格，将”%20”添加到res中，若不是空格，将当前字符添加到res

class Solution {
public:
    string replaceSpace(string s) {
        string res;
        for (auto c : s) {
            if (c == ' ')
                res += "%20";
            else
                res.push_back(c);
        }
        return res;
    }
};

思路二：双指针

首先扩充数组到每个空格替换成”%20”之后的大小。
然后从后向前替换空格，也就是双指针法，过程如下：
i指向新长度的末尾，j指向旧长度的末尾。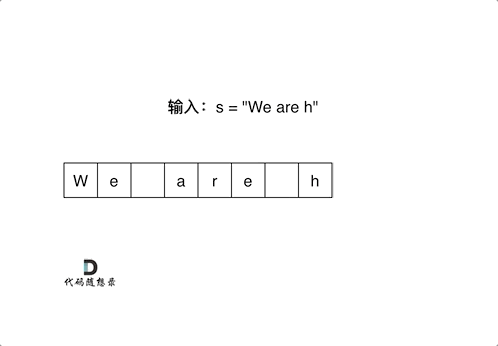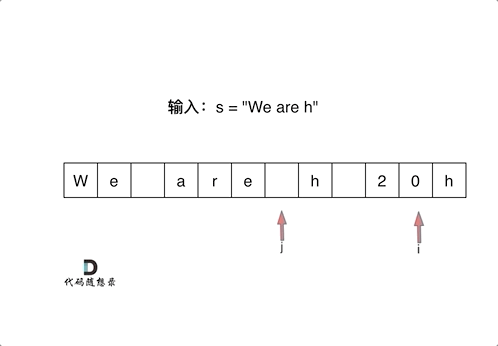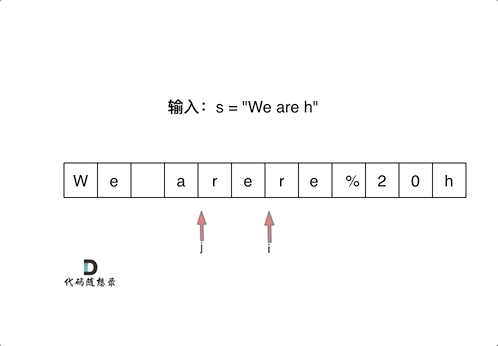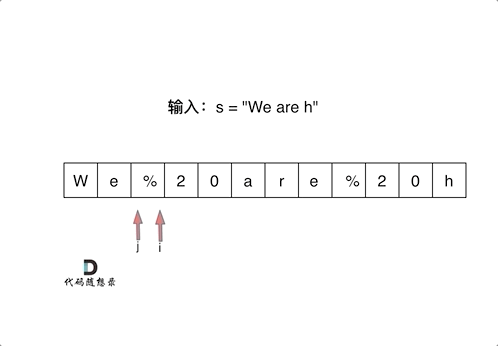

从前向后填充是O(n^2)的算法，因为每次添加元素都要将添加元素之后的所有元素向后移动。
其实很多数组填充类的问题，都可以先预先给数组扩容带填充后的大小，然后在从后向前进行操作。
这么做有两个好处：

1. 不用申请新数组。
2. 从后向前填充元素，避免了从前先后填充元素要来的 每次添加元素都要将添加元素之后的所有元素向后移动。

class Solution {
public:
    string replaceSpace(string s) {
        int cnt = 0;// 统计空格的个数
        int old = s.size();// 保留原字符串的长度
        for (auto c : s) 
            if (c == ' ')
                cnt++;
        s.resize(s.size() + 2 * cnt);
        for (int i = s.size() - 1, j = old - 1; j < i; i--, j--) {
            if (s[j] == ' ') {
                s[i--] = '0';
                s[i--] = '2';
                s[i] = '%';
            } else {
                s[i] = s[j];
            }
        }
        return s;
    }
};

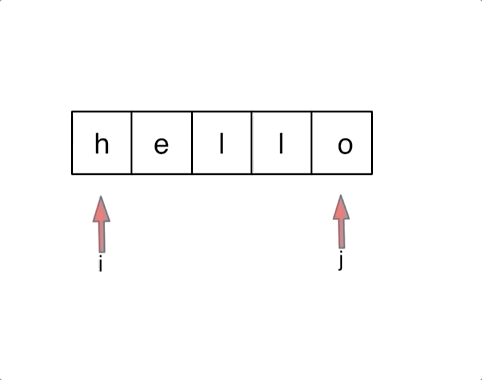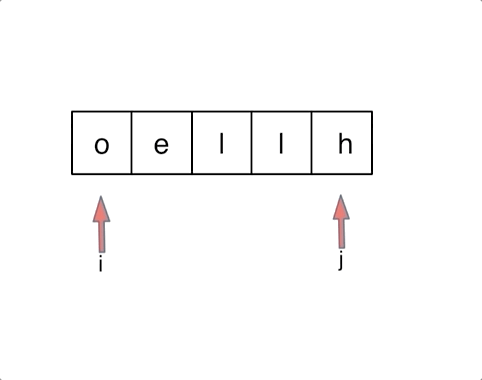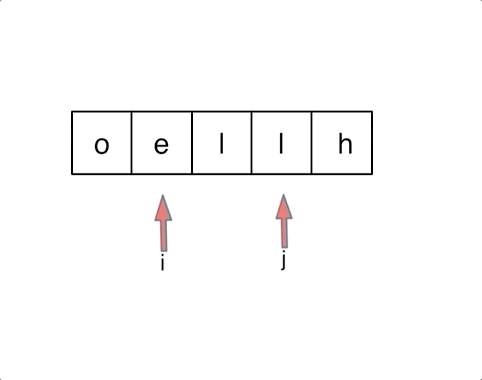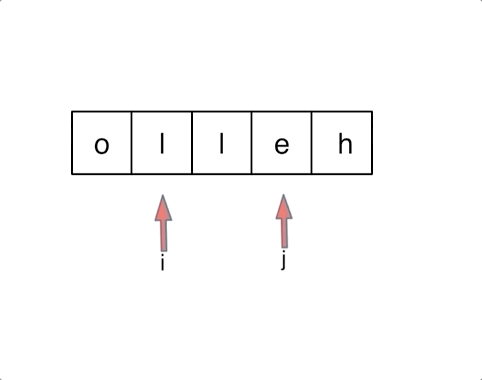
344. 反转字符串

思路一：双指针

void reverseString(vector<char>& s) {
    for (int i = 0, j = s.size() - 1; i < s.size()/2; i++, j--) {
        swap(s[i],s[j]);
    }
}

或者

class Solution {
public:
    void reverseString(vector<char>& s) {
        for (int i = 0; i < s.size() / 2; ++i) {
            swap(s[i], s[s.size() - i - 1]);
        }
    }
    // swap可以直接调用
    // void swap(char &a, char &b) {
    //     char tmp = a;
    //     a = b;
    //     b = tmp;
    // }
};

swap的实现方式

交换数值

int tmp = s[i];
s[i] = s[j];
s[j] = tmp;

位运算

s[i] ^= s[j];
s[j] ^= s[i];
s[i] ^= s[j];

541. 反转字符串 II

遍历字符串的过程中，只要让 i += (2 k)，i 每次移动 2 k 就可以了，然后判断是否需要有反转的区间。
所以当需要固定规律一段一段去处理字符串的时候，要想想在在for循环的表达式上做做文章。

class Solution {
public:
    string reverseStr(string s, int k) {
        for (int i = 0; i < s.size(); i += 2 * k) {
            // 剩余字符串大于k个，反转k个
            if (i + k <= s.size()) {
                reverse(s.begin() + i, s.begin() + i + k);
                continue;
            }
            // 剩余字符串小于k个，全部反转
            reverse(s.begin() + i, s.end());
        }
        return s;
    }
};

或者自己实现reserve

class Solution {
public:
    void reverse(string& s, int start, int end) {
        for (int i = start, j = end; i < j; i++, j--) {
            swap(s[i], s[j]);
        }
    }
    string reverseStr(string s, int k) {
        for (int i = 0; i < s.size(); i += (2 * k)) {
            // 1. 每隔 2k 个字符的前 k 个字符进行反转
            // 2. 剩余字符小于 2k 但大于或等于 k 个，则反转前 k 个字符
            if (i + k <= s.size()) {
                reverse(s, i, i + k - 1);
                continue;
            }
            // 3. 剩余字符少于 k 个，则将剩余字符全部反转。
            reverse(s, i, s.size() - 1);
        }
        return s;
    }
};

151. 翻转字符串里的单词

思路一：使用栈

这道题是将句子中的单词顺序反转，而单词本身字母的顺序是不变的，考虑使用栈，将每个单词压入栈中，然后从栈顶开始输出

class Solution {
public:
    string reverseWords(string s) {
       stack<string> stk;//保存单词
       for (int i = 0; i < s.size(); i++) {
           if (s[i] == ' ') continue;//找到第一个不为空格的字符
           string tmp;
           while (i < s.size() && s[i] != ' ') {
               tmp.push_back(s[i++]);
           }
           stk.push(tmp);
       }
       string res;
       while(!stk.empty()) {
           res += stk.top();
           stk.pop();
           res += ' ';
       }
       res.pop_back();//把最后一个空格删掉
       return res;
    }
};

思路二：直接生成res

从后往前遍历字符串，将单词逐个添加到结果中

class Solution {
public:
    string reverseWords(string s) {
        string res;
        for (int i = s.size() - 1; i >= 0; --i) { // 反向遍历
            if (s[i] == ' ')
                continue;
            int end = i; // 记住单词的结束位置
            while (i >= 0 && s[i] != ' ') {
                --i;
            }
            i++; // i重新指向单词的开头
            for (int j = i; j <= end; ++j) {
                res.push_back(s[j]);
            }
            res.push_back(' ');
        }
        res.pop_back(); // 弹出结尾的空格
        return res;
    }
};

思路三：原地解决

先移除多余的空格，然后将整个字符串翻转过来，然后翻转每个单词

所以解题思路如下：

• 移除多余空格
• 将整个字符串反转
• 将每个单词反转

举个例子，源字符串为：”the sky is blue “

• 移除多余空格 : “the sky is blue”
• 字符串反转：”eulb si yks eht”
• 单词反转：”blue is sky the”

class Solution {
public:
    // 移除多余的空格
    void removeSpace(string &s) {
        // 移除前面的空格
        int slow = 0, fast = 0;
        while (fast < s.size() && s[fast] == ' ') fast++;
        // 移动中间的空格
        while (fast < s.size()) {
            if (fast - 1 > 0 && s[fast] == s[fast - 1] && s[fast] == ' ') {
                fast++;
            } else {
                s[slow++] = s[fast++];
            }
        }
        // 移除尾部的空格
        if (slow - 1 > 0 && s[slow - 1] == ' ') {//最后一个字符为空格
            s.resize(slow - 1);
        } else {//最后一个字符不是空格
            s.resize(slow);
        }
    }

    //翻转字符串中的单词，左闭右闭
    void reverse(string &s, int begin, int end) {
        for (int i = begin, j = end; i < j; i++, j--) {
            swap(s[i], s[j]);
        }
    }

    string reverseWords(string s) {
        removeSpace(s);
        reverse(s, 0, s.size() - 1);
        for (int i = 0; i < s.size(); i++) {
                int begin = i, end = i;
                while (end < s.size() && s[end] != ' ') {
                    end++;
                    i++;//for循环上i再加一，正好将空格跳过
                }
                reverse(s, begin, end - 1);
        }
        return s;
    }

};

//主函数还可以再精简一点
string reverseWords(string s) {
    removeSpace(s);
    reverse(s, 0, s.size() - 1);
    for (int i = 0; i < s.size(); i++) {
        int j = i;
        while (j < s.size() && s[j] != ' ') j++;
        reverse(s, i, j - 1);
        i = j;
    }
    return s;
}

二刷新代码：

class Solution {
public:
    string reverseWords(string s) { 
        reverse(s.begin(), s.end());
        int index = 0;
        for (int i = 0; i < s.size(); ++i) { // 反向遍历
            if (s[i] == ' ') // 忽略空格
                continue;
            int start = i; // 记录单词的起始位置
            while (i < s.size() && s[i] != ' ') { 
                s[index++] = s[i++]; // 将单词移动到正确的位置，循环结束后，index指向单词后的空格
            }
            reverse(s.begin() + index - (i - start), s.begin() + index); // 反转单词，i - start是单词的长度
            s[index++] = ' '; // 单词后面添加空格
        }
        s.erase(s.begin() + index - 1, s.end()); // 将剩余部分删除，包括多添加的一个空格
        return s;
    }
};

28. 实现 strStr()

思路一：暴力查找

暴力查找没啥好说的，就是逐个字符比较，发现子串和模式有字符不匹配时，开始下一次匹配
时间复杂度O(MN) M、N分别是模式和主串的长度

这里只贴出代码，不写题解了

int ForceSubstrSearch1(string str, string pattern) {//暴力搜索算法1
    int n = str.size();
    int m = pattern.size();

    for (int i = 0; i < n - m + 1; i++) {
        int j;
        for (j = 0; j < m; j++) {
            if (str[i + j] != pattern[j])
                break;
        }
        if (j == m)
            return i;
    }

    return -1;
}

int ForceSubstrSearch2(string str, string pattern)
{//暴力搜索算法2
    int n = str.size();
    int m = pattern.size();

    int i, j;
    for (i = 0, j = 0; i < n && j < m; i++)
    {
        if (str[i] == pattern[j])
            j++;
        else
        {//回退
            i -= j;
            j = 0;
        }
    }
    if (j == m)
        return i - m;
    else
        return -1;
}

题解：

class Solution {
public:
    int strStr(string haystack, string needle) {
        if (needle.size() == 0)
            return 0;
        int m = haystack.size(), n = needle.size();
        for (int i = 0; i + n <= m; ++i) {
            int j = 0;
            while (j < n && haystack[i + j] == needle[j])
                ++j;
            if (n == j)
                return i;
        }
        return -1;
    }
};

思路二：KMP

讲解KMP的 我的博客
代码随想录

时间复杂度分析

其中n为文本串长度，m为模式串长度，因为在匹配的过程中，根据前缀表不断调整匹配的位置，可以看出匹配的过程是O(n)，之前还要单独生成next数组，时间复杂度是O(m)。所以整个KMP算法的时间复杂度是O(n+m)的。
暴力的解法显而易见是O(n m)，所以*KMP在字符串匹配中极大的提高的搜索的效率。
为了和力扣题目28.实现strStr保持一致，方便大家理解，以下文章统称haystack为文本串, needle为模式串。
都知道使用KMP算法，一定要构造next数组。

构造next数组

构造next数组其实就是计算模式串s，前缀表的过程。 主要有如下三步：

1. 初始化
2. 处理前后缀不相同的情况
3. 处理前后缀相同的情况

1. 初始化：

定义两个指针i和j，j指向前缀起始位置，i指向后缀起始位置。
然后还要对next数组进行初始化赋值，如下：

int j = -1;
next[0] = j;

j 为什么要初始化为 -1呢，因为之前说过 前缀表要统一减一的操作仅仅是其中的一种实现，我们这里选择j初始化为-1，下文我还会给出j不初始化为-1的实现代码。
next[i] 表示 i（包括i）之前最长相等的前后缀长度（其实就是j）
所以初始化next[0] = j 。

1. 处理前后缀不相同的情况

因为j初始化为-1，那么i就从1开始，进行s[i] 与 s[j+1]的比较。
所以遍历模式串s的循环下标i 要从 1开始，代码如下：

for(int i = 1; i < s.size(); i++) {

如果 s[i] 与 s[j+1]不相同，也就是遇到 前后缀末尾不相同的情况，就要向前回退。
怎么回退呢？
next[j]就是记录着j（包括j）之前的子串的相同前后缀的长度。
那么 s[i] 与 s[j+1] 不相同，就要找 j+1前一个元素在next数组里的值（就是next[j]）。
所以，处理前后缀不相同的情况代码如下：

while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
    j = next[j]; // 向前回退
}

1. 处理前后缀相同的情况

如果s[i] 与 s[j + 1] 相同，那么就同时向后移动i 和j 说明找到了相同的前后缀，同时还要将j（前缀的长度）赋给next[i], 因为next[i]要记录相同前后缀的长度。

if (s[i] == s[j + 1]) { // 找到相同的前后缀
    j++;
}
next[i] = j;

最后整体构建next数组的函数代码如下：

void getNext(int* next, const string& s){
    int j = -1;
    next[0] = j;
    for(int i = 1; i < s.size(); i++) { // 注意i从1开始
        while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
            j = next[j]; // 向前回退
        }
        if (s[i] == s[j + 1]) { // 找到相同的前后缀
            j++;
        }
        next[i] = j; // 将j（前缀的长度）赋给next[i]
    }
}

代码构造next数组的逻辑流程动画如下：

使用next数组来做匹配

在文本串s里 找是否出现过模式串t。
定义两个下标j 指向模式串起始位置，i指向文本串起始位置。
那么j初始值依然为-1，为什么呢？ 依然因为next数组里记录的起始位置为-1。
i就从0开始，遍历文本串，代码如下：

for (int i = 0; i < s.size(); i++)

接下来就是 s[i] 与 t[j + 1] （因为j从-1开始的） 进行比较。
如果 s[i] 与 t[j + 1] 不相同，j就要从next数组里寻找下一个匹配的位置。
代码如下：

while(j >= 0 && s[i] != t[j + 1]) {
    j = next[j];
}

如果 s[i] 与 t[j + 1] 相同，那么i 和 j 同时向后移动， 代码如下：

if (s[i] == t[j + 1]) {
    j++; // i的增加在for循环里
}

如何判断在文本串s里出现了模式串t呢，如果j指向了模式串t的末尾，那么就说明模式串t完全匹配文本串s里的某个子串了。
本题要在文本串字符串中找出模式串出现的第一个位置 (从0开始)，所以返回当前在文本串匹配模式串的位置i 减去 模式串的长度，就是文本串字符串中出现模式串的第一个位置。
代码如下：

if (j == (t.size() - 1) ) {
    return (i - t.size() + 1);
}

那么使用next数组，用模式串匹配文本串的整体代码如下：

int j = -1; // 因为next数组里记录的起始位置为-1
for (int i = 0; i < s.size(); i++) { // 注意i就从0开始
    while(j >= 0 && s[i] != t[j + 1]) { // 不匹配
        j = next[j]; // j 寻找之前匹配的位置
    }
    if (s[i] == t[j + 1]) { // 匹配，j和i同时向后移动
        j++; // i的增加在for循环里
    }
    if (j == (t.size() - 1) ) { // 文本串s里出现了模式串t
        return (i - t.size() + 1);
    }
}

前缀表统一减一 C++代码实现

class Solution {
public:
    void getNext(int* next, const string& s) {
        int j = -1;
        next[0] = j;
        for(int i = 1; i < s.size(); i++) { // 注意i从1开始
            while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
                j = next[j]; // 向前回退
            }
            if (s[i] == s[j + 1]) { // 找到相同的前后缀
                j++;
            }
            next[i] = j; // 将j（前缀的长度）赋给next[i]
        }
    }
    int strStr(string haystack, string needle) {
        if (needle.size() == 0) {
            return 0;
        }
        int next[needle.size()];
        getNext(next, needle);
        int j = -1; // // 因为next数组里记录的起始位置为-1
        for (int i = 0; i < haystack.size(); i++) { // 注意i就从0开始
            while(j >= 0 && haystack[i] != needle[j + 1]) { // 不匹配
                j = next[j]; // j 寻找之前匹配的位置
            }
            if (haystack[i] == needle[j + 1]) { // 匹配，j和i同时向后移动
                j++; // i的增加在for循环里
            }
            if (j == (needle.size() - 1) ) { // 文本串s里出现了模式串t
                return (i - needle.size() + 1);
            }
        }
        return -1;
    }
};

前缀表（不减一）C++实现

如果就直接使用前缀表可以换一种回退方式，找j=next[j-1] 来进行回退。
主要就是j=next[x]这一步最为关键！
我给出的getNext的实现为：（前缀表统一减一）

void getNext(int* next, const string& s) {
    int j = -1;
    next[0] = j;
    for(int i = 1; i < s.size(); i++) { // 注意i从1开始
        while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
            j = next[j]; // 向前回退
        }
        if (s[i] == s[j + 1]) { // 找到相同的前后缀
            j++;
        }
        next[i] = j; // 将j（前缀的长度）赋给next[i]
    }
}

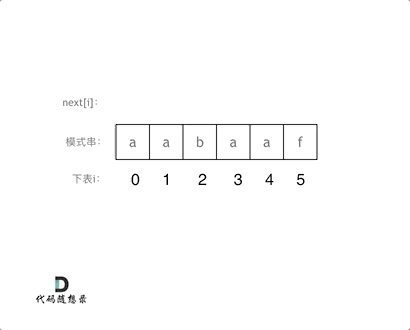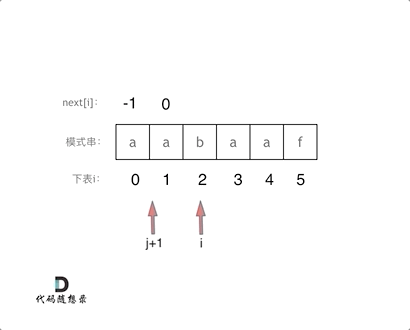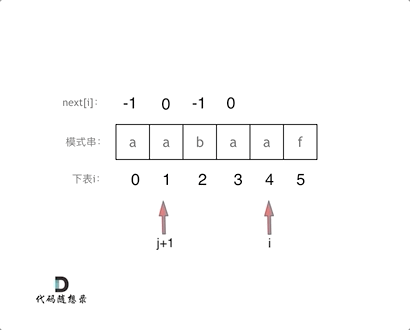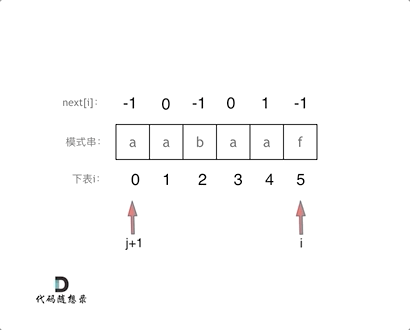
此时如果输入的模式串为aabaaf，对应的next为-1 0 -1 0 1 -1。
这里j和next[0]初始化为-1，整个next数组是以 前缀表减一之后的效果来构建的。
那么前缀表不减一来构建next数组，代码如下：

  void getNext(int* next, const string& s) {
        int j = 0;
        next[0] = 0;
        for(int i = 1; i < s.size(); i++) {
            while (j > 0 && s[i] != s[j]) { // j要保证大于0，因为下面有取j-1作为数组下标的操作
                j = next[j - 1]; // 注意这里，是要找前一位的对应的回退位置了
            }
            if (s[i] == s[j]) {
                j++;
            }
            next[i] = j;
        }
    }

此时如果输入的模式串为aabaaf，对应的next为 0 1 0 1 2 0，（其实这就是前缀表的数值了）。
那么用这样的next数组也可以用来做匹配，代码要有所改动。
实现代码如下：

class Solution {
public:
    void getNext(int* next, const string& s) {
        int j = 0;
        next[0] = 0;
        for(int i = 1; i < s.size(); i++) {
            while (j > 0 && s[i] != s[j]) {
                j = next[j - 1];
            }
            if (s[i] == s[j]) {
                j++;
            }
            next[i] = j;
        }
    }
    int strStr(string haystack, string needle) {
        if (needle.size() == 0) {
            return 0;
        }
        int next[needle.size()];
        getNext(next, needle);
        int j = 0;
        for (int i = 0; i < haystack.size(); i++) {
            while(j > 0 && haystack[i] != needle[j]) {
                j = next[j - 1];
            }
            if (haystack[i] == needle[j]) {
                j++;
            }
            if (j == needle.size() ) {
                return (i - needle.size() + 1);
            }
        }
        return -1;
    }
};

我的实现

class Solution {
public:
    int strStr(string haystack, string needle) {
        int i = 0, j = 0;
        vector<int> next = getNext(needle);
        while (i < haystack.size() && j < needle.size()) {
            if (haystack[i] == needle[j]) {
                i++;
                j++;
            } else if (j == 0) {
                i++;
            } else {
                j = next[j - 1];
            }
        }
        if (j == needle.size()) return i - j;
        else return -1;
    }

    vector<int> getNext(string needle) {
        int n = needle.size();
        vector<int> next(n, 0);
        int j = 0;
        for (int i = 1; i < n; ++i) {
            while (j > 0 && needle[i] != needle[j])
                j = next[j - 1];
            if (needle[i] == needle[j])
                j++;
            next[i] = j;
        }
        return next;
    }
};

代码随想录

459. 重复的子字符串

思路一：枚举

如果一个长度为 n 的字符串 s 可以由它的一个长度为 n’的子串 s’重复多次构成，那么：

• n一定是 n’ 的倍数；
• s’一定是 s的前缀；
• 对于任意的有

也就是说，s 中长度为 n’的前缀就是 s’，并且在这之后的每一个位置上的字符 s[i]，都需要与它之前的第 n’个字符 s[i-n’]相同。因此，我们可以从小到大枚举 n’，并对字符串 s 进行遍历，进行上述的判断。注意到一个小优化是，因为子串至少需要重复一次，所以 n’不会大于 n 的一半，我们只需要在的范围内枚举n即可。

class Solution {
public:
    bool repeatedSubstringPattern(string s) {
        int n = s.size();
        for (int i = 1; 2 * i <= n; ++i) { // 枚举重复子串的长度
            if (n % i == 0) { // 重复子串必须能够整除n
                bool match = true;
                for (int j = i; j < n; ++j) {
                    if (s[j] != s[j - i]) { // 对于每一个字符来说，如果重复，必有s[j] == s[j - 1]
                        match = false;
                        break;
                    }
                }
                if (match) {
                    return true;
                }
            }
        }
        return false;
    }
};

复杂度分析：

• 时间复杂度：O(n^2)：其中 n 是字符串 s的长度。枚举 i 的时间复杂度为 O(n)，遍历 s的时间复杂度为 O(n)，相乘即为总时间复杂度。
• 空间复杂度：O(1)

  思路二：字符串匹配

  我们可以把字符串 s 写成的形式，总计 个 s’。但我们如何在不枚举 n’的情况下，判断 s 是否能写成上述的形式呢？如果我们移除字符串 s 的前 n’个字符（即一个完整的 s’），再将这些字符保持顺序添加到剩余字符串的末尾，那么得到的字符串仍然是 s。由于 ，那么如果将两个 s 连在一起，并移除第一个和最后一个字符，那么得到的字符串一定包含 ，即 ss 是它的一个子串。
  因此我们可以考虑这种方法：我们将两个 ss 连在一起，并移除第一个和最后一个字符。如果 ss 是该字符串的子串，那么 s就满足题目要求。
  注意到我们证明的是如果 s 满足题目要求，那么 s 有这样的性质，而我们使用的方法却是如果 s 有这样的性质，那么 s 满足题目要求。因此，只证明了充分性是远远不够的，我们还需要证明必要性。

题解区的很多题解都忽略了这一点，但它是非常重要的。

这里先假设我们已经完成了证明，这样就可以使用非常简短的代码完成本题。在下面的代码中，我们可以从位置 11开始查询，并希望查询结果不为位置 n，这与移除字符串的第一个和最后一个字符是等价的

class Solution {
public:
    bool repeatedSubstringPattern(string s) {
        return (s + s).find(s, 1) != s.size();
    }
};

当然，还可以用kmp算法进行字符串的匹配

证明过程见官方题解

思路三：next数组

如果字符串可以由重复字串构成，把字符串 s 写成的形式，共n个,那么最大相等前后缀必然为，共n-1个 ，因为最大相等前后缀不包括字符串本身。那么用字符串的长度减去最大相等前后缀的长度，得到的就是一个的长度，也就是一个周期，所以，如果用字符串的长度减去最大相等前后缀的长度能够被字符串的长度整除，就说明该字符串有重复的字符串。

next 数组记录的就是最长相同前后缀，如果next[len - 1] != -1，则说明字符串有最长相同的前后缀（就是字符串里的前缀子串和后缀子串相同的最长长度）。
最长相等前后缀的长度为：next[len - 1] + 1。
数组长度为：len。
如果len % (len - (next[len - 1] + 1)) == 0 ，则说明 (数组长度-最长相等前后缀的长度) 正好可以被 数组的长度整除，说明有该字符串有重复的子字符串。
数组长度减去最长相同前后缀的长度相当于是第一个周期的长度，也就是一个周期的长度，如果这个周期可以被整除，就说明整个数组就是这个周期的循环。
强烈建议大家把next数组打印出来，看看next数组里的规律，有助于理解KMP算法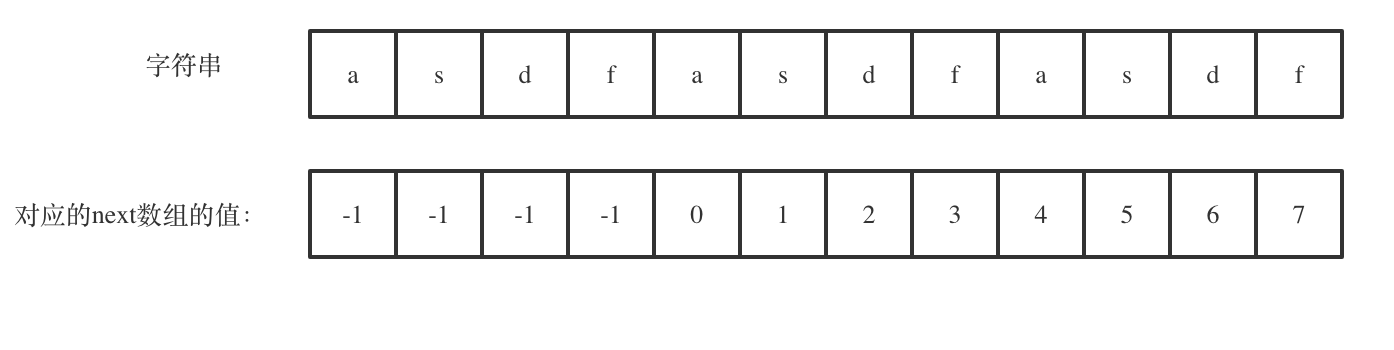

next[len - 1] = 7，next[len - 1] + 1 = 8，8就是此时字符串asdfasdfasdf的最长相同前后缀的长度。
(len - (next[len - 1] + 1)) 也就是： 12(字符串的长度) - 8(最长公共前后缀的长度) = 4， 4正好可以被 12(字符串的长度) 整除，所以说明有重复的子字符串（asdf）。
C++代码如下：（这里使用了前缀表统一减一的实现方式）

class Solution {
public:
    vector<int> getNext(string s) {
        vector<int> next(s.size(), -1);
        int j = -1;
        for (int i = 1; i < s.size(); i++) {
            while (j >= 0 && s[j + 1] != s[i]) {
                j = next[j];
            }
            if (s[j + 1] == s[i]) {
                j++;
            }
            next[i] = j;
        }
        return next;
    }

    bool repeatedSubstringPattern(string s) {
        int len = s.size();
        if (len == 0)
            return false;
        vector<int> next = getNext(s);
        if (next[len - 1] != -1 && len % (len - next[len - 1] - 1) == 0)
            return true;

        return false;
    }
};

3. 无重复字符的最长子串

思路一：滑动窗口

可以将无重复的子串看作一个窗口，用集合来记录窗口中的元素，遍历访问窗口的左端点，每次左端点左移都删除在集合中删除对应元素，如果右指针中的元素不在集合中，那么不断向集合中添加元素，扩大窗口，并记录窗口的最大长度

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        int maxLen = 0;
        unordered_set<int> us;
        for (int i = 0, j = -1; i < s.size(); i++) {
            if (i != 0) {
                us.erase(s[i - 1]); // 删除窗口左边的元素
            }
            // 如果右指针右边的元素未在集合中，那么添加该元素
            while (j + 1 < s.size() && !us.count(s[j + 1])) {
                us.insert(s[j + 1]);
                j++;
            }
            maxLen = max(maxLen, j - i + 1);
        }
        return maxLen;
    }
};

1044. 最长重复子串

思路一: 二分查找 + 字符哈希

子串的长度一定是在 1 ~ n - 1 范围内的, 可以看作递增序列，因此可以用二分查找来（加速）查找重复子串的最大长度
访问到当前长度时：

• 如果存在重复子串，那么更新最大重复子串的长度和起始位置，更新左边界（增大长度），查找是否有更长的重复字串
• 如果当前长度不存在重复子串，那么也不会有更长的重复子串了，更新右边界（减小长度）

通过上述分析，我们需要一个高效的算法来查找字符串中是否含有某长度的重复子串，采用字符串哈希法，将其映射为一个数值。
采用哈希映射必然会存在哈希值一样的情况出现，为了解决冲突，可以使用两个哈希映射或者用很大的数，两个哈希值都相同，才认为两串相等。

第一版本用一个哈希

class Solution {
public:
    // 判断字符串s中是否存在某长度的子串
    int check(const string &s, int len) {
        int R = 256; // 进制
        long long q = 10045000437; // 一个很大的数
        // 减第一位时用
        long long rm = 1;
        for (int i = 1; i < len; i++) {
            rm = (rm * R) % q;
        }
        unordered_set<long long> visited; // 记录访问过的哈希值
        // 计算第一个长度为len的串的哈希值
        long long hashValue = 0;
        for (int i = 0; i < len; i++) {
            hashValue = (hashValue * R + s[i]) % q;
        }
        visited.insert(hashValue);

        for (int i = len; i < s.size(); i++) {
            // 更新哈希值
            hashValue = (hashValue + q - s[i - len] * rm % q) % q;
            hashValue = (hashValue * R + s[i]) % q;
            if (visited.count(hashValue)) {
                return i - len + 1;
            }
            visited.insert(hashValue);

        }

        return -1;
    }

    string longestDupSubstring(string s) {
        int n = s.size();
        int left = 0, right = n; // 左闭右开
        int length = 0, start = -1; // 记录最长重复字串的长度和起始索引
        while (left < right) {
            int mid = left + ((right - left) >> 1); 
            int index = check(s, mid); 
            if (index != -1) { // 当前长度存在重复子串
                start = index; // 记录重复子串的起始位置
                length = mid;
                left = mid + 1; // 更新左边界
            } else {
                right = mid; // 更新右边界
            }
        }
        return start == -1 ? "" : s.substr(start, length);
    }
};

第二版，两个哈希映射

官方题解

typedef pair<long long, long long> pll;
class Solution {
public:
    long long pow(int a, int m, int mod) {
        long long ans = 1;
        long long contribute = a;
        while (m > 0) {
            if (m % 2 == 1) {
                ans = ans * contribute % mod;
                if (ans < 0) {
                    ans += mod;
                }
            }
            contribute = contribute * contribute % mod;
            if (contribute < 0) {
                contribute += mod;
            }
            m /= 2;
        }
        return ans;
    }

    int check(const vector<int> & arr, int m, int a1, int a2, int mod1, int mod2) {
        int n = arr.size();
        long long aL1 = pow(a1, m, mod1);
        long long aL2 = pow(a2, m, mod2);
        long long h1 = 0, h2 = 0;
        for (int i = 0; i < m; ++i) {
            h1 = (h1 * a1 % mod1 + arr[i]) % mod1;
            h2 = (h2 * a2 % mod2 + arr[i]) % mod2;
            if (h1 < 0) {
                h1 += mod1;
            }
            if (h2 < 0) {
                h2 += mod2;
            }
        }
        // 存储一个编码组合是否出现过
        set<pll> seen;
        seen.emplace(h1, h2);
        for (int start = 1; start <= n - m; ++start) {
            h1 = (h1 * a1 % mod1 - arr[start - 1] * aL1 % mod1 + arr[start + m - 1]) % mod1;
            h2 = (h2 * a2 % mod2 - arr[start - 1] * aL2 % mod2 + arr[start + m - 1]) % mod2;
            if (h1 < 0) {
                h1 += mod1;
            }
            if (h2 < 0) {
                h2 += mod2;
            }

            // 如果重复，则返回重复串的起点
            if (seen.count(make_pair(h1, h2))) {
                return start;
            }
            seen.emplace(h1, h2);
        }
        // 没有重复，则返回-1
        return -1;
    }

    string longestDupSubstring(string s) {
        srand((unsigned)time(NULL));
        // 生成两个进制
        int a1 = random()%75 + 26;
        int a2 = random()%75 + 26;

        // 生成两个模
        int mod1 = random()%(INT_MAX - 1000000006) + 1000000006;
        int mod2 = random()%(INT_MAX - 1000000006) + 1000000006;
        int n = s.size();
        // 先对所有字符进行编码
        vector<int> arr(n);
        for (int i = 0; i < n; ++i) {
            arr[i] = s[i] - 'a';
        }
        // 二分查找的范围是[1, n-1]
        int l = 1, r = n - 1;
        int length = 0, start = -1;
        while (l <= r) {
            int m = l + (r - l + 1) / 2;
            int idx = check(arr, m, a1, a2, mod1, mod2);
            if (idx != -1) {
                // 有重复子串，移动左边界
                l = m + 1;
                length = m;
                start = idx;
            } else {
                // 无重复子串，移动右边界
                r = m - 1;
            }
        }
        return start != -1 ? s.substr(start, length) : "";
    }
};

我的版本

typedef pair<long long, long long> pairll;
class Solution {
public:

    // 判断字符串s中是否存在某长度的子串
    int check(const string &s, int len, int r1, int r2, int mod1, int mod2) {
        // 减第一位时用
        long long rm1 = 1, rm2 = 1;
        for (int i = 1; i < len; i++) {
            rm1 = (rm1 * r1) % mod1;
            rm2 = (rm2 * r2) % mod2;
        }
        set<pairll> visited; // 记录访问过的哈希值
        // 计算第一个长度为len的串的哈希值
        long long hashValue1 = 0, hashValue2 = 0;
        for (int i = 0; i < len; i++) {
            hashValue1 = (hashValue1 * r1 + s[i]) % mod1;
            hashValue2 = (hashValue2 * r2 + s[i]) % mod2;
        }
        visited.emplace(hashValue1, hashValue2);

        for (int i = len; i < s.size(); i++) {
            // 更新哈希值1
            hashValue1 = (hashValue1 + mod1 - s[i - len] * rm1 % mod1) % mod1;
            hashValue1 = (hashValue1 * r1 + s[i]) % mod1;
            // 更新哈希值2
            hashValue2 = (hashValue2 + mod2 - s[i - len] * rm2 % mod2) % mod2;
            hashValue2 = (hashValue2 * r2 + s[i]) % mod2;

            if (visited.count(make_pair(hashValue1, hashValue2))) {
                return i - len + 1;
            }
            visited.emplace(hashValue1, hashValue2);
        }

        return -1;
    }


    string longestDupSubstring(string s) {
        srand((unsigned)time(NULL));

        // 生成两个进制
        int r1 = random() % 99 + 26;
        int r2 = random() % 99 + 26;

        // 生成两个模
        int mod1 = random() % (INT_MAX - 1000000006) + 1000000006;
        int mod2 = random() % (INT_MAX - 1000000006) + 1000000006;

        int n = s.size();
        int left = 0, right = n; // 左闭右开
        int length = 0, start = -1; // 记录最长重复字串的长度和起始索引
        while (left < right) {
            int mid = left + ((right - left) >> 1); 
            int index = check(s, mid, r1, r2, mod1, mod2); 
            if (index != -1) { // 当前长度存在重复子串
                start = index; // 记录重复子串的起始位置
                length = mid;
                left = mid + 1; // 更新左边界
            } else {
                right = mid; // 更新右边界
            }
        }
        return start == -1 ? "" : s.substr(start, length);
    }
};

(哈希表)720. 词典中最长的单词

见注释

class Solution {
public:
    string longestWord(vector<string>& words) {
        // 先将字典按照长短排序，如果一样长的单词，按照字典序降序排序，这样保证后遍历的一定是长度最长且字典序最小的单词
        sort(words.begin(), words.end(), [](const string &s1, const string& s2) {
            if (s1.size() != s2.size()) {
                return s1.size() < s2.size();
            } else {
                return s1 > s2;
            }
        });
        unordered_set<string> us;
        string res = ""; // 空字符串满足要求
        us.emplace(""); // 
        for (auto& word : words) {
            if (us.count(word.substr(0, word.size() - 1))) { // 如果word的前缀在集合里，那么word满足要求
                us.emplace(word);
                res = word;
            }
        }
        return res;
    }
};